Tutorial Harmonische Analyse
Dieses Tutorial behandelt die von FlexPro angebotenen Spektralverfahren zur Harmonischen Modellierung und zur Messung der Harmonischen Verzerrung.
Fourier-Analyse
Falls Sie sich bisher das Fourier-Analyse-Tutorial und das Spektralschätzer-Tutorial noch nicht angesehen haben, sollten Sie dies jetzt tun. Der erste Schritt der Harmonischen Analyse ist eine voll automatisierte Spektralschätzung, die typischerweise durch Fourier-Analyse, AR-Spektralschätzer oder Eigenwertanalyse erfolgt.
Ein harmonisches Testsignal mit Verzerrungen und Rauschen
Für dieses Tutorial wird ein Signal mit 1024 Werten verwendet. Das Signal besitzt eine Grundwelle und eine Reihe von Oberwellen bei den Vielfachen der Frequenz der ersten Harmonischen:
100.0*sin(2π*x*250+p/4)
10.0*sin(2π*x*500+p/2)
1.0*sin(2π*x*750+p)
0.1*sin(2π*x*1000+3p/2)
0.01*sin(2π*x*1250+7p/4)
Die Abtastrate beträgt 5000 Hz, die Nyquist-Frequenz, die maximale Frequenz, die ausgewertet werden kann, liegt daher bei 2500 Hz. Die Zeitwerte variieren von 0 bis 0,2046 bei einem Abtastintervall von 0,0002. Es wird 0,01 % weißes Rauschen hinzugefügt. Das führt zu einem Hintergrundrauschen bei einem Pegel von -100 dB bezogen auf den größten Peak.
Wählen Sie Datei > Projektdatenbank öffnen und öffnen Sie die Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Tutorials\Spectral Analysis.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021>Examples>Tutorials>Spectral Analysis.fpd. Öffnen Sie den Ordner Tutorials und darin den Unterordner Harmonic Analysis und öffnen Sie das 2D-Diagramm Data per Doppelklick.
Hier sehen Sie die Abbildung des Signals, das über 1024 Fließkommawerte verfügt.
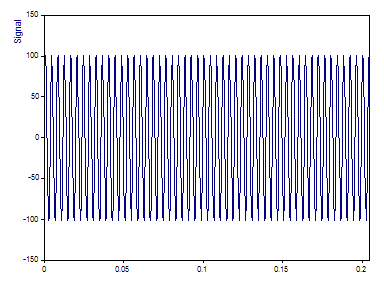
Nur die Grundwelle ist im Zeitbereich erkennbar. Die Oberwellen verursachen eine signifikante harmonische Verzerrung.
Sehen Sie sich zunächst das Fourier-Spektrum des Signals an, obwohl es möglich ist, die Anzahl der harmonischen Komponenten ohne dieses zu bestimmen.
Fourier-Spektren
Schließen Sie die Abbildung und markieren Sie den Datensatz Signal.
Klicken Sie auf Einfügen[Analysen] > Analyse-Assistent.
Wählen Sie die Kategorie Fourier-Analyse unter Spektralanalysen aus. Dort wählen Sie Fourier-Spektrum aus. Klicken Sie auf die Weiter-Schaltfläche
Als Spektrumtyp wählen Sie dB, normiert. Als Fenstertyp wählen Sie Chebyshev und geben als einstellbaren Parameter 4 ein. Stellen Sie sicher, dass die FFT-Länge auf 16384 gesetzt ist. Wählen Sie die Maximale Peak-Anzahl Option und geben Sie dort den Wert 5 ein. Setzen Sie anschließend Kritische Grenze Weißes Rauschen % auf Keine. Falls über den Peaks keine Beschriftungen sichtbar sind, klicken Sie auf Beschriftungen, bis die Dezibelwerte erscheinen.
Die Darstellung des Fourier-Spektrums im Analyseassistenten sollte folgendermaßen aussehen:
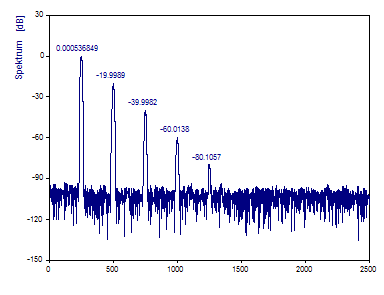
Die Oberwellen werden durch das Fourier-Spektrum ausreichend charakterisiert.
Klicken Sie auf Beschriftungen, bis die Frequenzen angezeigt werden.
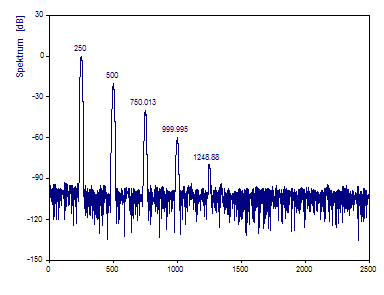
Die Frequenzen der Grundwelle als auch der Oberwellen werden also von diesem optimierten Fourier-Spektrum hinreichend geschätzt.
Fourier-Methoden für Frequenzidentifizierung
Die Einstellungen, die für das Fourier-Spektrum verwendet wurden, repräsentieren die Einstellungen, die bei der Harmonischen Analyse automatisch verwendet werden. Die Harmonische Analyse verwendet die Fourier-Analyse für die Frequenzidentifizierung. In allen Fällen wird das Tschebyscheff-Bewertungsfenster benutzt und dessen einseitige Breite des Hauptmaximums automatisch gesetzt. Für Daten der Länge 256 und weniger wird die Breite auf 2 gesetzt. Für Datenlängen über 1024 ist die Fensterbreite 4. Zwischen diesen Werten variieren die Fenstereinstellungen logarithmisch mit (-6+1.4427ln(n)). So wird eine Frequenzbereichsbreite von 3 für eine Datensatzlänge von 512 verwendet. Das Anhängen von Nullen (zero padding) wird benutzt, um eine FFT-Länge von 16384 zu erhalten, falls die Datensatzlänge kleiner als 16384 sein sollte.
Es gibt zwei Vorbehalte, die Fourier-Analyse für die Frequenzidentifizierung zu verwenden. Die exakte Spektralschätzung kann schlechter als die AR-Prozedur oder die Eigenwertanalyse sein, selbst wenn Bewertungsfenster, Anhängen von Nullen und Band-Interpolation eingesetzt werden. Dies gilt vor allem dann, wenn der Datensatz nur tausend oder weniger Punkte hat. Fourier-Analyse für Frequenzidentifizierung wird nicht empfohlen, falls der Datensatz sehr klein ist, d.h. wenige hundert Werte hat.
Genauso wichtig ist der Punkt, dass die Fourier-Analyse oft am Auf- und Abstieg eines großen Peaks einige scharfe Nebenmaxima verursacht. Das Tschebyscheff-Fenster wurde benutzt, um diesen Effekt zu minimieren. Er kann dennoch auftreten, insbesondere beim Anhängen von Nullen zur Verbesserung der Frequenzschätzung. Obwohl die Harmonische Analyse auch einige Komponenten aufnehmen kann, die zwar nur Rauschen modellieren aber dadurch die Genauigkeit der Modellierung für die Signalkomponenten verbessern, sollte doch sichergestellt sein, dass solche parasitären Peaks auf den Schultern der Haupt-Peaks nicht in das Modell eingehen.
Dies ist das Fourier-Spektrum, genau wie oben, außer dass das -92 dB Blackman-Harris-Fenster eingesetzt wurde. 10 Peaks werden erkannt.
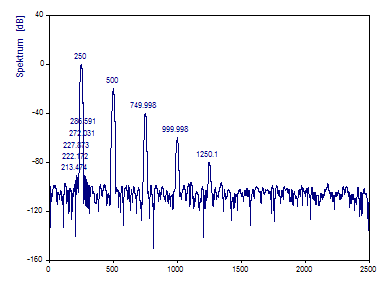
Sie sehen, dass die fünf zusätzlichen Peaks alle im Bereich des Peaks der ersten Harmonischen auftauchen. In solch einem Fall ist es nicht möglich, zusätzliche Harmonische hinzuzufügen, um Rauschen nachzubilden. Hier ist es wichtig, dass nur fünf Harmonische in das Modell aufgenommen werden.
Harmonische Schätzung
Das Ziel der Harmonischen Analyse ist es, ein Signal mit schmalbandigen Sinuskurven oder gedämpften Sinuskurven zu modellieren. Das Ergebnis der Analyse ist eine gewisse Anzahl an Harmonischen, die durch Amplitude, Frequenz, Phase und, im Falle von gedämpften Sinuskurven, Dämpfungsfaktor definiert sind.
Klicken Sie auf Zurück. Wählen Sie die Kategorie Harmonische Analysen unter Spektralanalyse aus. Dort wählen Sie Harmonische Schätzung aus. Klicken Sie auf die Weiter-Schaltfläche. Wählen Sie als Algorithmus Fourier und als Modell Sinusförmig. Setzen Sie die Komponentenanzahl auf Als maximale Anzahl und geben Sie 10 ein. Der Ergebnistyp ist Harmonische Komponenten. Klicken Sie auf Beschriftungen, bis die Amplitudenbeschriftung erscheint.
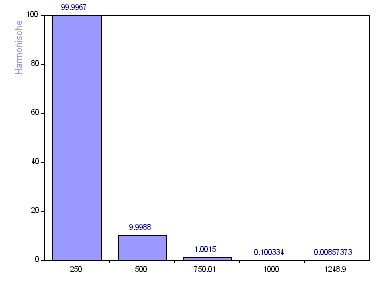
Obwohl es möglich ist, die Amplitudenwerte aus der Beschriftung abzulesen, ist dies keine gute Darstellung. Es wird eine logarithmische Skalierung benötigt, um den breiten Dynamikbereich der Amplituden sauber darzustellen.
Klicken Sie auf die Weiter-Schaltfläche, um zu Schritt 3 des Assistenten zu gelangen. Aktivieren Sie das oberste Kontrollfeld und wählen Sie anschließend das 2D-Diagramm mit dem Namen Harmonische. Wählen Sie die logarithmische Y-Achse. Klicken Sie auf Zurück, um wieder zu Schritt 2 des Assistenten zu gelangen.
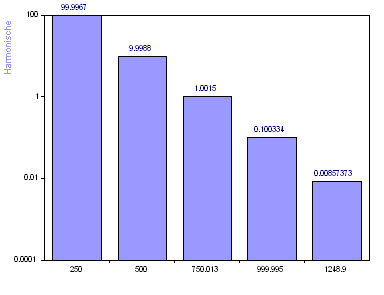
Die Harmonische Modellierung besteht aus zwei Schritten. Der erste Schritt, die Fourier-Analyse, wird nur zur Schätzung der Frequenzen, bei denen Spektralkomponenten auftreten, verwendet. Die Amplituden- oder Leistungsinformationen des Fourier-Spektrums werden bei der Harmonischen Analyse nicht verwendet. In diesem Fall wurde die Fourier-Analyse zur Bestimmung der 10 Frequenzen der bedeutendsten Spektralkomponenten verwendet. Das hier abgebildete Harmonische Spektrum basiert auf einer linearen Approximation von Sinuskurven im Zeitbereich. Die ersten vier Amplituden wurden sehr gut bestimmt. Die fünfte Harmonische hat einen Fehler größer als 10 %. Die restlichen Harmonischen modellieren das im Signal vorhandene Rauschen. Da weißes Rauschen gleichmäßig über alle Frequenzen verteilt ist, dies jedoch hier nicht entsprechend modelliert wird, sollte die Anzahl an Harmonischen auf die Zahl der tatsächlichen Spektralkomponenten reduziert werden.
Obwohl die fünf Peaks des Signals bei der visuellen Untersuchung des Fourier-Spektrums klar ersichtlich waren, ist dies bei der Harmonischen Analyse basierend auf den aus dem Fourier-Spektrum ermittelten Spektralfrequenzen nicht so eindeutig. Es gibt keine klare Abgrenzung zwischen Signal und Rauschen.
Wählen Sie den AR Datenmatrix VR SVD-Algorithmus. Setzen Sie die Modellordnung auf 40.
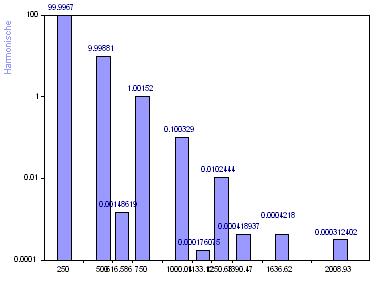
Wenn der AR SVD-Algorithmus für die Frequenzidentifizierung verwendet wird, gibt es fünf eindeutige Komponenten über dem Hintergrundrauschpegel. Ferner werden die Amplituden durch die linearen Sinusfunktionen besser bestimmt, da die Frequenzen besser geschätzt werden. Die zusätzlichen Harmonischen sind außerdem gleichmäßiger über alle Frequenzen verteilt, wie es vom zufälligen Rauschen erwartet wird.
Wählen Sie den Eigenwertanalyse MUSIC-Algorithmus.
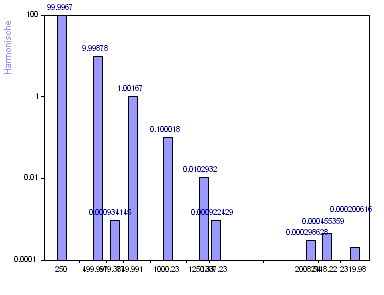
Wenn der Eigenwertanalyse MUSIC Algorithmus für die Frequenzidentifizierung verwendet wird, gibt es ebenfalls fünf eindeutige Komponenten über dem Hintergrundrauschpegel. Die Genauigkeit der Amplitudenbestimmung ähnelt der der AR-Methode.
Die AR SVD Methode verwendet die Signal-Eigenmoden zur Spektralschätzung. Die Eigenwertanalyse verwendet grundsätzlich Rausch-Eigenmoden zur Spektralschätzung. Eine von beiden kann zu einem exakteren Ergebnis führen. Deshalb sollten oft beide Fälle untersucht werden. Beachten Sie, dass die fünf Signalfrequenzen von beiden Prozeduren gut erkannt werden. Die fünf Harmonischen zur Rauschmodellierung haben eine geringe Überlappung.
Parameter der Harmonischen Komponenten
Weißes Rauschen sollte unkorreliert sein. Das bedeutet, dass sich über die Tendenz oder die Fortdauer des Rauschsignals keine Aussagen treffen lassen. Die Rauschamplitude an einer diskreten Frequenz sollte sich in keiner Weise auf die Amplitude der nächsten Frequenz auswirken. Falls Rauschen vollständig unkorreliert ist, haben die zusätzlichen Harmonischen, die zur Rauschanpassung verwendet werden, keinen Nutzen.
Um nur die ersten fünf Signalkomponenten zu modellieren, setzen Sie Maximalanzahl auf 5.
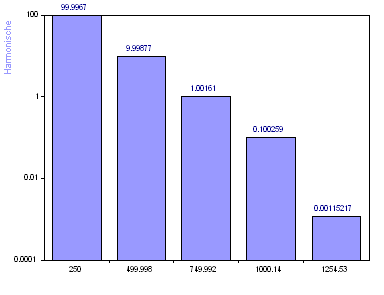
Sie sehen, dass die leistungsärmste Oberwelle (Amplitude 0,01) nicht mehr exakt geschätzt wird. Tatsächlich ist ihre Amplitude gegenüber dem wahren Wert um fast ein Zehntel gefallen. Während wir bei zehn angegebenen Harmonischen fünf für die Modellierung des Rauschsignals zur Verfügung haben, haben wir jetzt nur noch die fünf gegenwärtigen Signalkomponenten. Das Rauschen beeinflusst die leistungsärmste Oberwelle nachteilig.
Setzen Sie Maximalanzahl zurück auf 10. Klicken Sie auf Weiter. In Schritt 3 wählen Sie die ersten beiden Optionen aus und klicken auf Beenden. Doppelklicken Sie auf HarmonischeAnalyse.
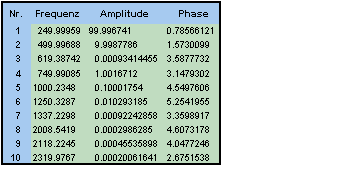
Die Frequenzen, Amplituden und Phasen der fünf Signalkomponenten wurden ziemlich genau geschätzt. Typisch bei der Harmonischen Modellierung ist die Tatsache, dass die Frequenzen den kleinsten Fehler und die Phasen den größten Fehler aufweisen. Die Amplitudenfehler liegen dazwischen. Je größer die Leistung einer Komponente ist, desto exakter lassen sich die Parameter, die die Harmonischen definieren, bestimmen.
Harmonische Verzerrung
Der Klirrfaktor (THD = total harmonic distortion) ist das Verhältnis der Wurzel der Summe aller Leistungen bzw. quadrierten Amplituden der Oberwellen zur Amplitude der Grundwelle.
Gewöhnlich werden FFTs zur Messung des Klirrfaktors verwendet. Wegen des Überlaufs auf benachbarte Spektralwerte bei der Fensterung oder wegen des Leckeffekts, der auftritt, wenn kein Bewertungsfenster eingesetzt wird, ist die Berechnung des exakten Klirrfaktors unter Verwendung der FFT sehr schwierig. Das gilt vor allem, wenn das Rauschen ignoriert werden soll und nur die Oberwellen im Signal einbezogen werden sollen.
FlexPro's Harmonische Modellierung macht es möglich, eine exakte Schätzung des wahren Klirrfaktors (THD) zu erzielen. Der wahre Wert für dieses Testsignal ist sqrt(10²+1²+0,1²+0,01²) / 100. Das sind 10,05%.
Die Einstellungen, die für die Harmonische Modellierung benutzt wurden, können ebenfalls bei einem Klirrfaktorenspektrum benutzt werden.
Markieren Sie den Datensatz Signal.
Klicken Sie auf Einfügen[Analysen] > Analyse-Assistent.
Wählen Sie die Kategorie Harmonische Analysen unter Spektralanalyse aus. Dort wählen Sie Harmonische Schätzung aus. Klicken Sie auf die Weiter-Schaltfläche.
Wählen Sie den Algorithmus Eigenwertanalyse MUSIC und das Modell Sinusförmig. Setzen Sie die Komponentenanzahl Als maximale Anzahl auf 5. Als Spektrumtyp wählen Sie Klirrfaktorenspektrum in %. Klicken Sie auf Beschriftungen, bis die Verzerrungen in % angezeigt werden.
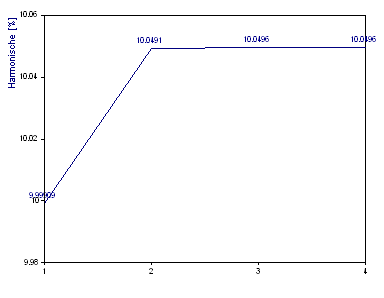
Die Nummer der Komponenten wird auf der x-Achse angezeigt. Bei der 2. Komponente ist die harmonische Verzerrung entsprechend dem Verhältnis der ersten Oberwelle zur Grundwelle dargestellt. Bei Komponente 3 wird die kumulierte Verzerrung, die aus der ersten und zweiten Oberwelle resultiert, dargestellt. Deshalb ist der Wert an Position 4 der Klirrfaktor (THD) ohne Rauschen. Der Wert 10,0497 ist sehr nah am korrekten Wert 10,0504. Wenn Sie die Anzahl der Komponenten auf 10 hoch setzen, sehen Sie, dass die fünf zusätzlichen Harmonischen zur Rauschmodellierung nicht entscheidend zum Klirrfaktor beitragen.
Klicken Sie auf Beenden, um den Analyseassistenten zu schließen.