Tutorial Fourier-Spektralanalyse
Dieses Tutorial behandelt Fourier-Spektralanalyse in FlexPro für den Fall, dass Komponenten mit sehr wenig Leistung von im weiteren Sinne stationären Signalen untersucht werden sollen, und dass Spektralschätzungen mit kleiner Varianz gewünscht werden.
Ein passendes Testsignal
Für dieses Tutorial wird ein Signal verwendet, das vier Sinuskurven mit gleicher Leistung, die sich über den Nyquist-Bereich erstrecken und drei Sinuskurven niedriger Leistung, die sich dazwischen befinden, enthält. Die Komponenten mit niedriger Leistung liegen -40 dB, -50 dB und -60 dB unter den Referenzsinuskurven. Außerdem wird weißes Rauschen so hinzugefügt, dass sich das Hintergrundrauschen bei ungefähr -75 dB befindet. Das Ziel dieses Tests ist die exakte Frequenz- und Leistungsschätzung dieser drei leistungsarmen Komponenten. Ein weiterer Gesichtspunkt wird die Ermittlung der Phasen-Informationen dieser Komponenten sein.
Die sieben Sinuskurven sehen folgendermaßen aus:
1.0*sin(2π*x*1005+p/2)+ (0dB)
1.0*sin(2π*x*2005+p/2)+ (0dB)
1.0*sin(2π*x*3005+p/2)+ (0dB)
1.0*sin(2π*x*4005+p/2)+ (0dB)
0.01*sin(2π*x*1505+p/2)+ (-40dB)
0.003162*sin(2π*x*2505+3p/2)+ (-50dB)
0.001*sin(2π*x*3505+p) (-60dB)
Der X-Wert (Zeit) variiert von 0 bis 0,1 bei einer Schrittweite von 0,0001. Die Nyquist-Frequenz ist somit 5000 (Hälfte der Abtastfrequenz von 10000). Die vier Referenzsinuskurven erstrecken sich über den Nyquist-Bereich. Die erste Sinuskurve mit geringer Leistung (-40dB) hat 1% der Amplitude der Referenzsinuskurven und 0,01 % Leistung von einer der Refererenzsinuskurven. Die zweite Sinuskurve geringer Leistung (-50dB) hat 0,001 % der Leistung der Referenzkurven. Die letzte Testkurve (-60 dB) hat nur 0,1% der Amplitude und 0,0001 % der Leistung der Referenzkurven. Gauss-Rauschen (bei 0,15 %) wurde hinzugefügt, um ein Hintergrundrauschen bei ungefähr -75 dB zu erzeugen. Es sollte folglich möglich sein mittels geeigneter Spektralanalyse sogar die -60dB Komponente auswerten zu können.
Wählen Sie Datei > Projektdatenbank öffnen und öffnen Sie die Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Tutorials\Spectral Analysis.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021>Examples>Tutorials>Spectral Analysis.fpd. Öffnen Sie den Ordner Tutorials und darin den Unterordner Fourier Spectral Analysis und öffnen Sie das 2D-Diagramm Data per Doppelklick.
Dies ist die Abbildung des Signals mit 1001 Fließkomma-Werten.
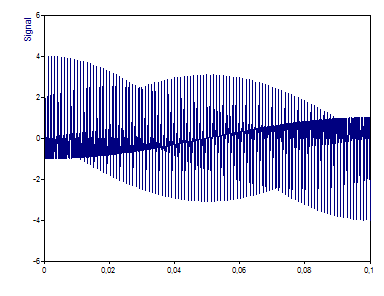
Das unbewertete Fourier-Spektrum
Für die Fourier-Spektralanalyse mit hohem Dynamikbereich werden fast immer Bewertungsfenster verwendet. Um zu sehen, warum das so ist, schauen Sie sich zunächst eine einfache, unbewertete FFT an.
Schließen Sie das Diagramm und markieren Sie den Datensatz Signal.
Klicken Sie auf Einfügen[Analysen] > Analyse-Assistent.
Wählen Sie die Kategorie Fourier-Analysen unter Spektralanalysen aus. Dort wählen Sie Fourier-Spektrum aus. Klicken Sie auf die Weiter-Schaltfläche.
Der Schritt 2 des Analyseassistenten enthält einen interaktiven Dialog, in dem mehrere Prozeduren optimiert und verglichen werden können, mit dem Ziel einer best möglichen Analyse. Beginnen Sie mit der Betrachtung des unbewerteten Fourier-Spektrums.
Beachten Sie, dass unter Spektralprozedur die Option Fourier-Spektrum ausgewählt ist. Obwohl die Spektralprozedur schon in Schritt 1 ausgewählt wurde, kann sie in Schritt 2 verändert werden.
Wählen Sie als Spektrumtyp den Wert dB, normiert.
So wird der größte Peak im Spektrum auf 0 dB normiert. Alle anderen Peaks haben dann einen negativen Wert. Ein Peak bei -3 dB hätte halb so viel Leistung wie ein Peak bei 0 dB und ein Peak bei -6 dB hätte eine halb so große Amplitude.
Als Fenstertyp wählen Sie Rechteck -13dB W=1.
Im Spektralanalyse-Modul werden alle festen, nicht einstellbaren Bewertungsfenster durch ihren Namen, die Abschwächung der Nebenmaxima in dB und die einseitige Breite des Hauptmaximums aufgelistet. Eine Rechteckfensterung entspricht keiner Fensterung, da alle Datenelemente mit Eins multipliziert werden.
Stellen Sie sicher, dass die FFT-Länge auf Datenlänge bzw. 1001 gesetzt wird.
Das Nullen anhängen-Informationsfeld zeigt, dass kein Anhängen von Nullen (zero padding) stattgefunden hat.
Wählen Sie Maximale Peak-Anzahl unter Optionen und geben dort den Wert 7 ein.
Der Analyseassistent erzeugt automatisch Information über die Peaks des Spektrum. Ist die Option auf 7 eingestellt, so werden die sieben Peaks mit der größten Leistung angezeigt. Beachten Sie bitte, dass es auch möglich ist, einen dB-Schwellenwert unter dem höchsten Peak anzugeben. Für diesen Datensatz könnten Sie einen -65 dB Schwellenwert einstellen.
Setzen Sie jetzt Kritische Grenze Weißes Rauschen % auf Keine.
Später werden Sie das Testen kritischer Grenzen am Signal ausprobieren.
Falls über den Peaks keine Beschriftungen sichtbar sind, Klicken Sie auf Beschriftungen, bis die Amplituden-Beschriftungen erscheinen.
Sie können zwischen mehreren Zuständen umschalten. Sie können die Beschriftung für die Y-Komponente des Spektrums (hier in dB, normiert) oder für die X-Komponente (immer Frequenzen) einschalten. Alternativ können Sie die Beschriftungen auch abschalten.
Die Fourier-Grafik im Analyseassistenten sollte folgendermaßen aussehen:
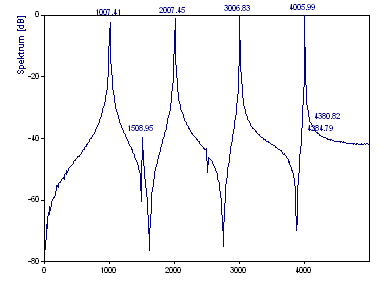
Die FFT-Berechnung verwendet den schnellst möglichen FFT-Algorithmus, der die Daten exakt transformiert. In diesem Fall wird der Primfaktor-FFT-Algorithmus verwendet, da es sich um die schnellste FFT-Prozedur handelt, die den Datensatz mit den 1001 Werten berechnet. Das erzeugte Fourier-Spektrum erfasst die vier Referenzpeaks. Der -40 dB Peak wird abgebildet. Es gibt nur eine Andeutung des -50 dB Peak und kein Anzeichen vom -60 dB Peak. Obwohl die Frequenzen der Peaks im Spektrum mit einer kubischen Spline-Interpolation zentriert werden, werden die Bezugsfrequenzen 1005, 2005, 3005 und 4005 nicht exakt wiedergegeben.
Beachten Sie, dass die vier Referenz-Peaks eine deutlich unterschiedliche Form haben. Die Peaks werden schärfer, wenn sich die Frequenz erhöht. Das ist kein Ergebnis der Frequenz, sondern des Leckeffekts auf benachbarte Frequenzlinien im Spektrum. Je besser eine harmonische Komponente innerhalb der Frequenzlinien zentriert ist, desto schärfer wird die FFT Frequenzantwort sein.
Wählen Sie die obere Grafik und klicken Sie auf die Cursor aktivieren-Schaltfläche. Setzen Sie den Cursor auf den ersten Peak.
Beachten Sie, dass die tatsächliche Frequenz des ersten Peak mit dem Wert 1005 innerhalb der FFT-Frequenzlinien 999 und 1009 untergebracht sein muss. Die Frequenz 4005 des vierten Peaks kann größtenteils in der FFT-Frequenzlinie 4006 untergebracht sein. Nur wenn eine Frequenz genau auf eine Frequenzlinie fällt, kann eine harmonische Komponente durch einen einzelnen FFT-Kanal repräsentiert werden.
Klicken Sie auf noch einmal Cursor aktivieren, um das Cursorn auszuschalten. Ändern Sie die FFT-Länge auf 8192.
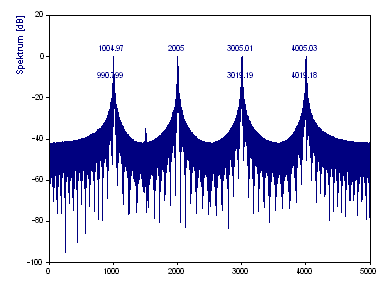
Durch Anhängen von Nullen wird das FFT-Spektrum vergrößert. Es gibt nun näherungsweise achtmal so viele Frequenzen innerhalb des Spektrums. Die band-interpolierten Frequenzen der Referenzschwingungen sind jetzt exakt bestimmt, aber die drei Komponenten mit den niedrigen Leistungen gehen auf der Grundlinie verloren. Der Leckeffekt vergrößert sich, da das Anhängen von Nullen zu einer Unstetigkeit am Ende des Datensatzes führt.
Geben Sie 2000 im Feld FFT-Länge ein erzwingen Sie eine Aktualisierung, indem Sie das Feld mit der Tab-Taste verlassen.
So wird eine FFT mit exakten 5 Hz Abstandsintervallen erzeugt. Die Frequenzen aller sieben Sinuskurven liegen jetzt genau im Zentrum einer FFT-Spektrallinie.
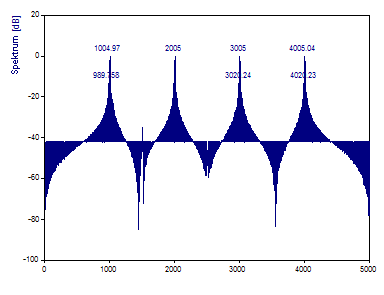
Die Peaks im Spektrum sind jetzt Impulsfunktionen, aber der durch das Anhängen von Nullen verursachte Leckeffekt reicht aus, um die drei Komponenten niedriger Leistung zu verdecken. Ohne Bewertungsfenster ist es nicht möglich, die Komponenten niedriger Leistung zu ermitteln.
Fensterbewertetes Fourier-Spektrum
Ein Bewertungsfenster reduziert den Betrag der Datenwerte auf 0 an jedem Ende eines Datensatzes. Während dies den Einfluss der Daten im Zentrum eines Datensatzes vergrößert und den Einfluss der Daten am Rand vermindert, entfernt es die Unstetigkeiten am Rand der Daten. Wenn die Daten in einem Bildumlauf-Format angezeigt würden, würde eine Stetigkeit an dem Ort beobachtet, wo sich zwei Enden treffen.
Ein Bewertungsfenster hat auch Auswirkungen im Frequenzbereich. Das Bewertungsfenster hat eine Frequenzantwort, die die Peaks eines Spektrums verbreitert und so deren Auflösung reduziert. Harmonische Komponenten geringer Leistung werden ebenfalls eingeführt. Der Nutzen ist eine erhebliche Reduktion der Leckeffekte, was wiederum das Anhängen von Nullen in beliebigem Maß ermöglicht.
FlexPro führt eine Leistungsnormierung durch, wenn ein Bewertungsfenster verwendet wird. Die Leistung eines fensterbewerteten Fourier-Spektrums ist identisch mit der Leistung seines unbewerteten Gegenstücks. Auf der anderen Seite nimmt die Höhe der Peaks des Spektrums als Konsequenz aus der Fensterung trotz der Leistungsnormierung etwas ab. Wenn ein Bewertungsfenster verwendet wird, ist es zwar immer noch möglich, die relative Leistung zu beurteilen, indem eine normierte dB-Skalierung verwendet wird. Aber es ist nicht länger möglich, die absoluten Amplituden oder Leistungen direkt aus den Höhen der Peaks des Spektrums auszulesen.
Verändern Sie den Fenstertyp auf Cos4 Blackman-Harris -92dB W=4 und setzen Sie FFT-Länge auf 8192.
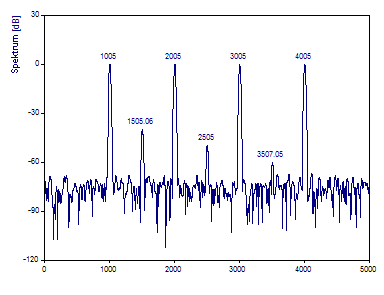
Klicken Sie auf die Beschriftungen-Schaltfläche, um die Beträge der Spektren als Beschriftungen anzuzeigen.
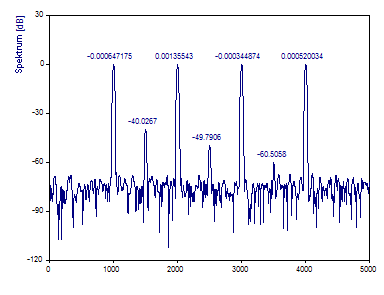
Das Blackman-Harris Fenster ist für die Fourier-Spektralanalyse mit hohem Dynamikbereich sehr beliebt. Die sieben Referenzkurven werden sowohl in ihrer Frequenz als auch in ihrer Leistung exakt abgebildet.
Beachten Sie, dass ein genauer 0 dB Peak nicht vorhanden ist. Die Null dB Normierung verwendet die tatsächlichen Spektralwerte. Die ausgegebenen Peaks sind jedoch band-interpoliert und der Peak mit der größten Leistung liegt etwas über 0 dB.
Bewertungsfenster
Es ist eine Kunst, ein passendes Bewertungsfenster auszuwählen. In FlexPro gibt es zwanzig feste Fenster und neun Fenster, dessen Eigenschaften sich über einen einstellbaren Parameter beeinflussen lassen.
Die Breite des Hauptmaximums (mainlobe width), die in der Auswahlliste als Parameter W aufgeführt wird, hat eine direkte Beziehung zur Frequenzauflösung. Ein Fenster mit einer spektralen Breite von 3 hat nur ein Drittel der Frequenzauflösung eines unbewerteten Fourier-Spektrums. Der Sidelobe-Wert, ebenfalls in der Auswahlliste aufgeführt, ist der Wert in dB, um den das größte Nebenmaximum unter dem Hauptmaximum liegt. Je größer dieser Wert ist, desto größer ist die Wahrscheinlichkeit, einen Peak geringer Leistung aufzulösen, der dicht bei einer Komponente hoher Leistung liegt. Ein anderer Faktor bei der Auswahl der Fenster ist der Rolloff-Wert. Je größer der Rolloff, desto größer ist die Wahrscheinlichkeit, eine Komponente niedriger Leistung weit entfernt vom ersten Peak des Spektrums aufzulösen. Der Sidelobe-Wert ist ein Maß für den auftretenden Leckeffekt als Ganzes und der Rolloff-Wert gibt an, wie dieser sich auf das Spektrum verteilt.
Der erste Kompromiss ist die Auflösung gegenüber dem Dynamikbereich, was durch die spektrale Breite (main lobe width) bestimmt wird. Der zweite Kompromiss ist die Auflösung benachbarter Peaks gegenüber weit auseinander liegender Peaks. Dies wird durch den Sidelobe-Wert und den Rolloff charakterisiert.
Das Tschebyscheff-Fenster produziert den schärfsten Peak des Spektrums für einen gegebenen Sidelobe-Wert. Es handelt sich um ein geeignetes Bewertungsfenster für die Auflösung nah beieinander liegender Komponenten unterschiedlicher Leistung. Das Cosine Maximum Rolloff-Fenster erzeugt die schnellste Kosinus-basierte Dämpfung im Frequenzbereich, was es möglich macht, Peaks mit sehr geringer Leistung und in einiger Entfernung vom ersten Peak zu analysieren. Das Kaiser-Bessel-Fenster ist ein sehr gut einstellbares Fenster und somit ein sehr guter Kompromiss zwischen den beiden Extrema.
Eine Besonderheit stellt das Flattop-Fenster dar. Dieses weist zwar eine Breite des Hauptmaximums von 5 auf, bietet also eine relativ geringe spektrale Auflösung, dafür hat das Hauptmaximum jedoch im vollen Bereich von einer Frequenzlinie bis zu deren linken und rechten Nachbar nahezu den gleichen Betrag. Das Hauptmaximum weist also eine zwar breite aber dafür flache Spitze auf. Dieses Fenster eignet sich damit insbesondere zum Ausmessen der Leistungen bzw. Amplituden schmalbandiger Signalkomponenten, d. h. einzelner Peaks im Spektrum. Die Höhe eines Peaks wird nämlich durch die spezielle Form des Hauptmaximums nahezu unabhängig von dessen Lage zwischen zwei Frequenzlinien.
Signifikanzniveaus
FlexPro bietet Peak-basierte kritische Grenzen, um zu bestimmen, ob ein Peak statistisch bedeutsam ist oder nicht. Die Referenz ist weißes (normalverteiltes) Rauschen. Eine 95 % kritische Grenze ist das Niveau, bei dem nur bei einem der zwanzig einzelnen Zufallsrauschsignale der größte vorhandene Peak aufgrund des Zufallsprinzips diese Höhe erreichen würde. Eine 99,9 % kritische Grenze ist entsprechend das Niveau, bei dem nur bei einem der tausend einzelnen zufälligen Rauschsignalen der größte Peak diese Höhe erreichen würde.
Die kritischen Grenzen basieren auf umfassenden Monte Carlo Versuchen, welche mit den implementierten Algorithmen und Anpassungen durchgeführt wurden. Es werden unterschiedliche Modelle zur Berechnung der kritischen Grenze für jedes der in FlexPro verwendeten Bewertungsfenster verwendet. Für die anpassbaren Fenster werden 3D-Oberflächenmodelle verwendet. Da dieser Ansatz den Abfall der Peak-Höhe bei Verwendung von Bewertungsfenstern berücksichtigt, sind die kritischen Grenzen für alle Bewertungsfenster, einschließlich der mit verstellbaren Parametern, korrekt.
Ändern Sie Kritische Grenze Weißes Rauschen auf 99.9%.
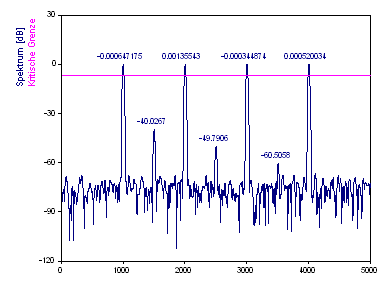
Bei diesem Datensatz ist der größte Peak mit einer Sicherheit von mehr als 99,9 % bedeutsam. Dieser Test vergleicht nur die Komponente, die die größte Leistung hat, mit dem Gauß-Rauschen. Es kann hieraus kein Rückschluss auf die anderen Peaks getroffen werden.
Referenzen
Für Vergleichszwecke wird dieses Diagramm als Referenz festgehalten.
Klicken Sie dazu auf die Referenz setzen-Schaltfläche.
Die Referenz ersetzt die Abbildung des Datensatzes. Beachten Sie, dass die Kritischen Grenzen und die Peaks nicht in den Referenzen enthalten sind.
Spektralanalyse mit Niedriger Varianz
Im Folgenden werden die Spektralprozeduren von FlexPro für solche Fälle vorgestellt, bei denen eine Spektralschätzung mit niedriger Varianz benötigt wird. Es wird angenommen, dass die Genauigkeit der Leistungsmessung höchste Priorität hat.
Reduzierung der Varianz der Spektralmaße
Die Varianz einer FFT verringert sich nicht, wenn sich die Datenlänge vergrößert. Stattdessen ist die Varianz eine Konstante, deren Quadratwurzel (Standardabweichung) ungefähr gleich der mittleren Leistung des Signals ist. Um die Varianz einer FFT-basierten Spektralschätzung zu verringern, werden Mittelwertbildung und orthogonale Bewertungsfenster-Techniken verwendet.
Periodogramm (Überlappend-segmentiertes Fourier-Spektrum)
In FlexPro gibt es zwei Fourier-Prozeduren, um Schätzungen des Spektrums mit verringerter Varianz zu erzeugen. Die erste dieser Methoden ist das "Periodogramm". Für eine stationäre Datenreihe sollte jeder Ausschnitt die gleichen spektralen Eigenschaften aufweisen. Es ist daher möglich, eine Serie von FFTs aufzusummieren, um eine Spektralschätzung mit verringerter Varianz zu erzeugen. Die FFTs werden mittels eines Schiebefensters (eine kleinere Segmentgröße), das sich mit einem angegebenen Maß an Überlappung über die Datenreihe bewegt, berechnet. Die FFT geringerer Größe resultiert in einer geringeren Auflösung. Die Auflösung wird zugunsten geringerer Schwankungen des Ergebnisses der Spektralschätzung geopfert.
Wählen Sie für die Spektralprozedur die Option Periodogramm aus. Verwenden Sie weiterhin als Spektrumtyp die Einstellung dB, normiert. Wählen Sie das Tschebyscheff-Fenster und setzen die einseitige Fourierbreite mit Fensteranpassung auf 4,0. Setzen Sie, falls nötig, die Segmentlänge auf den Standardwert Datenlänge/4, die FFT-Länge auf 4096 und Überlappung % auf 90. Falls über den Peaks keine Beschriftungen sichtbar sind, klicken Sie auf Beschriftungen, bis die Amplituden-Beschriftungen erscheinen.
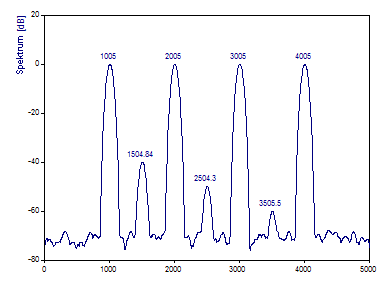
Klicken Sie auf Beschriftungen, damit die spektralen Leistungsdichten in dB angezeigt werden.
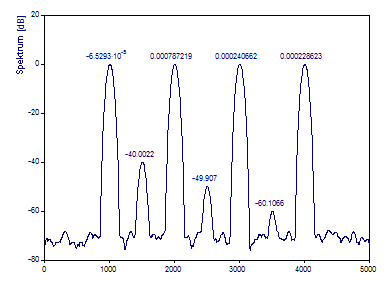
Bei einer Segmentlänge von 250 Werten (1/4 Datensatzlänge) und einer Überlappung von 90 % existieren 31 diskrete Segmente, die kombiniert ein Spektrum mit niedriger Varianz liefern. Da die Segmentlänge nur ein Viertel der gesamten Datensatzlänge entspricht, verringert sich die Auflösung im Frequenzbereich proportional. Deshalb sind die Peaks im Periodogramm breiter. Aber es gibt 31 individuelle Fourier-Spektren, die summiert das gesamte Periodogramm erzeugen. Aus diesem Grund werden die Leistungen der drei leistungsarmen Peaks genauer erfasst.
Das Tschebyscheff-Fenster wurde hier verwendet, weil es ein konstantes weißes Hintergrundrauschen über alle Frequenzen verteilt gibt. Ein Fenster mit hohem Rolloff (schnellem Abklingen der Nebenmaxima) hat hier keine Vorteile. Falls rotes Rauschen (Rauschen, das sich bei höheren Frequenzen verkleinert) vorhanden wäre, wäre ein Fenster mit großem Rolloff, wie Beta oder Cosine Maximum Rolloff eine bessere Wahl.
Die Optimierung der Segmentgröße und der Überlappung ist nicht immer eine dankbare Aufgabe. Generell liefert eine große Anzahl Segmente keine wesentliche Verbesserung der Varianz. Typischerweise gibt es keine deutliche Verminderung der Varianz jenseits einer Überlappung bei 50 bis 70%, egal, ob Bewertungsfenster verwendet werden oder nicht.
Amplituden und Bewertungsfenster
Dies ist ein guter Zeitpunkt, die Auswirkungen eines Bewertungsfensters auf die Amplitude zu beobachten.
Ändern Sie den Fenstertyp auf Rechteck -13dB W=1 (keine Fensterung), die Normierung auf Keine und ändern Sie den Spektrumtyp auf Amplitude.
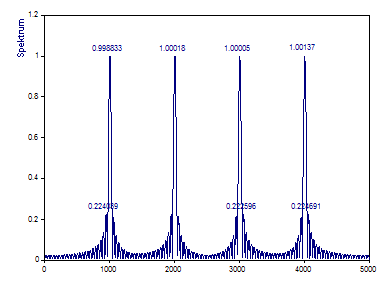
Beachten Sie, dass die Amplituden der vier Referenzsinuskurven, jede von ihnen hat die Amplitude 1, wegen der hohen Überlappung sehr exakt wiedergegeben werden.
Ändern Sie Fenstertyp auf Cos2 Hamming -43dB W=2.
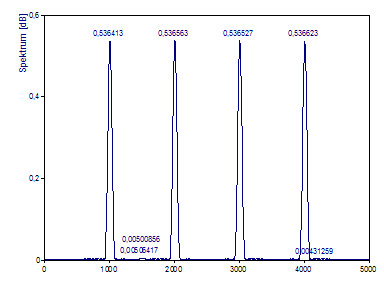
Das Hamming-Fenster ist ein Cosinus-Fenster mit minimaler Höhe des Nebenmaximums und einer einseitigen Breite des Hauptmaximums von 2 Spektrallinien. Sie sehen, dass sich die Amplituden der Peaks um ungefähr 50% verringert haben. Für den Fall, dass das Spektrum aus abgegrenzten Peaks besteht, hängt diese Verminderung nur von der gewählten Fensterfunktion ab und kann daher einfach kompensiert werden.
Ändern Sie die Normierung auf Amplitude.
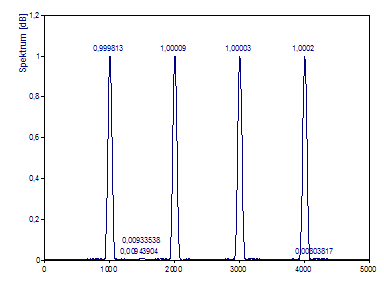
Die Amplituden der Peaks stimmen nun wieder exakt mit denen der Referenzschwingungen im Signal überein. Die Amplitudennormierung verwendet den Gewinn der gewählten Fensterfunktion, d. h. die Summe über die Quadrate der Werte der Fensterfunktion, dividiert durch deren Anzahl, als Normierungsfaktor. Bitte beachten Sie jedoch, dass diese Art der Normierung nicht sicherstellt, dass die Gesamtenergie im Spektrum gleich der des Zeitsignals ist. Für Fälle, in denen dies gefordert ist, steht Ihnen die Normierungsart Leistung zur Verfügung.
Optimierung des Periodogramms
Ändern Sie Fenstertyp auf Cos3 Minimum Sidelobe -71dB W=3.
Der Dämpfungswert von -71dB dieses Fensters sollte zu einem ausreichenden Dynamikbereich führen, um die drei Peaks mit niedriger Leistung entdecken zu können.
Ändern Sie Spektrumtyp auf dB, normiert.
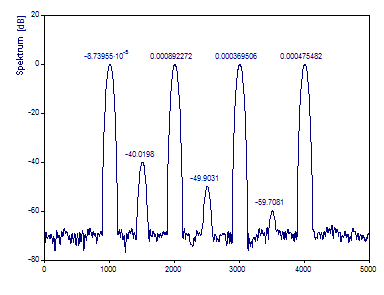
Sie sehen, dass die drei Schmalband-Komponenten mit niedriger Leistung tatsächlich bei Verwendung dieses Bewertungsfensters aufgelöst werden. Die Peaks sind außerdem bei diesem Fenster der Breite 3 schärfer als bei dem Tschebyscheff-Bewertungsfenster der Breite 4, das zuvor verwendet wurde. Obwohl es für dieses Beispiel nicht zutrifft, gibt es Fälle, bei denen nah beieinander liegende Spektralkomponenten ein Fenster benötigen, dessen Sidelobe-Wert gerade unter dem Hintergrundrauschen der Daten liegt. Beachten Sie, dass die einstellbaren Fenster kontinuierlich sind und es daher möglich ist, irgendeine gewünschte gebrochene Fourier-Breite zu setzen.
Ändern Sie den Fenstertyp auf Tschebyscheff und setzen Sie die einseitige Fourier-Breite Fensteranpassung auf 2.9.
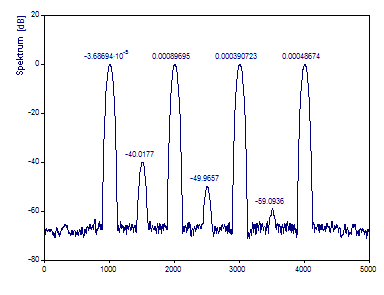
Die Abbildung zeigt eine fast optimale Fensterung für die Minimierung der Breite der Peaks. Die Peaks haben die minimale Breite, um leistungsarme Komponenten gegenüber dem Hintergrundrauschen ausfindig machen zu können. Das sind allerdings nicht notwendigerweise die optimalen Einstellungen für das Periodogramm. Wenn ein wenig von der verbesserten Varianz geopfert wird, ist ein schärferes Spektrum möglich.
Wählen Sie 500 aus dem Segmentlänge-Auswahlfeld und behalten Sie für Überlappung % den Wert 90 bei.
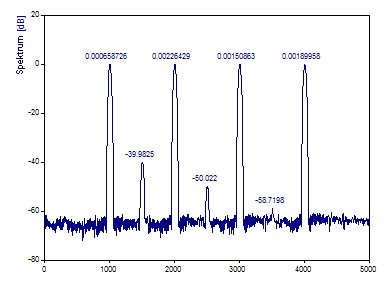
Wenn diese Einstellungen verwendet werden, werden 11 Fourier-Spektren der halben Länge zur Erzeugung des Periodogramms benutzt. Beachten Sie, dass die Peaks jetzt wesentlich schärfer sind. Die größere Varianz im verrauschten Bereich des Spektrums ist ebenso offensichtlich wie die sehr ungenaue Abbildung der leistungsarmen Komponenten.
Multitaper-Spektralanalyse
Die zweite Methode in FlexPro, um reduzierte Varianzspektren zu erzeugen, ist die Multitaper-Prozedur. Bei einer Multitaper-Prozedur wird ein Satz orthogonaler Bewertungsfenster auf die Daten angewandt und die Spektren werden in bestimmter Weise gemittelt, um ein zusammengesetztes Spektrum zu erhalten. Im Gegensatz zum Segment-überlappenden Verfahren, das nur einen Teil des Datensatzes für jedes individuelle Spektrum gebraucht, benutzt die Multitaper-Prozedur den gesamten Datensatz mit jedem Bewertungsfenster.
Eine Multitaper-Prozedur ähnelt ein wenig der Mittelung der Spektren aus einer Vielzahl an Bewertungsfenstern. In diesem Fall gäbe es mit Sicherheit eine Redundanz, da die verschiedenen Bewertungsfenster stark miteinander korrelieren (alle haben ähnliche Peak-Formen). Die orthogonalen Bewertungsfenster, die beim Multitaper-Spektrum verwendet werden, sind jedoch, im Gegensatz zu den konventionellen Bewertungsfenstern, unkorreliert. Nur das erste Bewertungsfenster besitzt die bekannte Form.
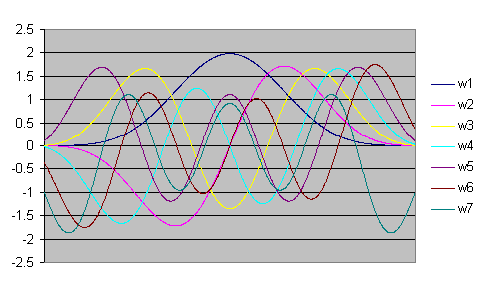
Die Spektren der unterschiedlichen Bewertungsfenster erzeugen keinen gemeinsamen zentralen Peak für eine harmonische Komponente. Nur das erste Bewertungsfenster produziert einen zentralen Peak bei der harmonischen Frequenz der Komponente. Die anderen Bewertungsfenster erzeugen Peaks, die leicht nach oben oder unten in der Frequenz abweichen. Jedes der Spektren trägt seinen Teil zum Gesamtspektrum bei.
Die Vorteile der Multitaper-Analyse liegen darin, dass keine Auflösung geopfert wird und es keinen Informationsverlust an den Rändern des Datensatzes gibt. Während es tatsächlich zu einem Informationsverlust an den Rändern des ersten Bewertungsfensters kommt, sind die entsprechenden Daten in den folgenden Fenstern enthalten und hervorgehoben. Die Form der den einzelnen Komponenten zugeordneten Spektralpeaks macht die relative Leistungsbestimmung zu einer einfachen Sache. Der Nachteil liegt darin, dass die spektrale Hülle, die jeder Komponente zugeordnet ist, keine scharfe Frequenzauflösung bietet.
Die Mutlitaper-Prozedur führt immer eine Leistungsnormierung für das Ergebnisspektrum durch. Die Auswahlen Keine und Leistung in der Liste Normierung führen daher zum gleichen Ergebnis. Die Normierungsart Amplitude kann jedoch wie beim Periodogramm dazu eingesetzt werden, um die Amplitudendämpfung von Peaks im Spektrum zu kompensieren. Die Normierungsfaktoren wurden empirisch als Funktion der Anzahl der Fenster und der Fensterbreite ermittelt.
Wählen Sie Multitaper-Spektrum als Spektralprozedur und wählen Sie den Spektrumtyp dB, normiert. Setzen Sie die einseitige Fourier-Breite (Fensteranpassung) auf 3,0. Geben Sie für Anzahl der DPSS-Fenster den Wert maximal oder 5 ein. Setzen Sie FFT-Länge auf 4096. Klicken Sie auf Beschriftungen, bis die Frequenzen über den Peaks erscheinen.
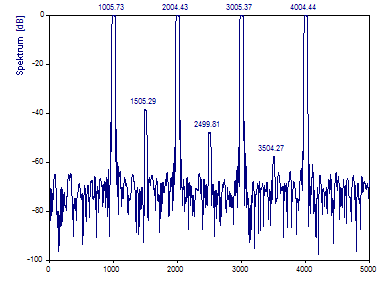
Beachten Sie die abgeflachte Form der Peaks. Die Form der Peaks macht es leicht, die relative Spektralleistung zu erkennen, aber schwierig, die Mittenfrequenz der Peak-Hülle zu lokalisieren. FlexPro verwendet die Peak-Positionen im F-Werte Spektrum zum Bestimmen der Peak-Frequenzen. Die F-Werte sind ein Maß für die Signifikanz und haben keinen direkten Bezug zur Varianz.
Klicken Sie auf die Beschriftungen-Schaltfläche, um sich die Spektraldichte in dB anzeigen zu lassen.
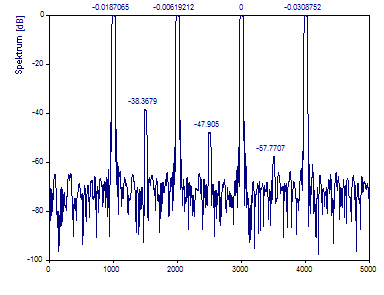
Sie sehen, dass das Mitteln der Spektren der orthogonalen Bewertungsfenster, im Gegensatz zum Periodogramm, nicht zu einem glatteren Hintergrundrauschen führt.
Da die Multitaper-Hülle keine sauber definierten Peaks hat, kann das Maximum im Spektrum nicht exakt bestimmt werden. Das ist ein möglicher Grund, weshalb alle drei leistungsarmen Peaks im normierten Spektrum um +2dB abweichen.
Ein wichtiger Hinweis für die Multitaper-Spektralanalyse betrifft die Anzahl der zu verwendenden Bewertungsfenster. Für eine einseitige Fourieranalyse mit einer Breite von 3,0 unterstützt FlexPro bis zu 5 Bewertungsfenster. Für eine Breite von 4,0 können bis zu 7 DPSS-Bewertungsfenster verwendet werden. Der Dynamikbereich der individuellen DPSS Bewertungsfenster verringert sich mit dem Sequenzfortschritt. Das erste-DPSS Bewertungsfenster, w1 in der Abbildung, ist ein exzellentes Bewertungsfenster und bietet den besten Dynamikbereich der Sequenz an (es handelt sich um das anpassbare Slepian-Fenster der Fourieranalyse und der Periodogramm-Prozedur). Jedes nachfolgende Fenster in der DPSS-Folge bietet einen verringerten Dynamikbereich. Wenn ein großer Dynamikbereich gewünscht wird, ist es oft am besten, das letzte oder die letzten beiden Fenster in der Sequenz auszuschließen. Beispielsweise ist für eine Fourier-Breite von 3 eine Gesamtanzahl an Bewertungsfenstern von 3 oder 4 die beste Wahl. Für ein Spektrum mit einer Fourier-Breite von 4 würden 5 Fenster das beste Ergebnis liefern.
Ändern Sie Anzahl der DPSS-Fenster auf 3.
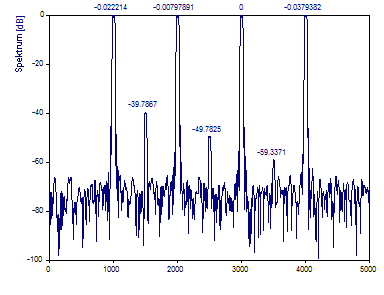
Sie sehen, dass die Peaks genauer werden.
Amplitudendämpfung im Multitaper-Spektrum
Ändern Sie Anzahl der DPSS-Fenster auf 5 oder maximal, die Normierung auf Leistung und ändern Sie Spektrumtyp auf Amplitude.
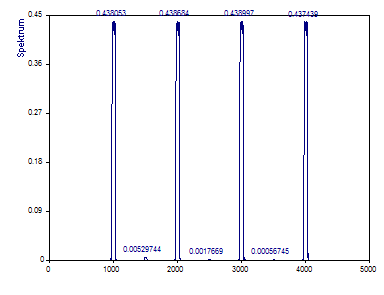
Für ein Periodogramm mit einem Bewertungsfenster der Fourier-Breite 3 ist die Amplitudendämpfung ungefähr 24% (76% der tatsächlichen Amplitude wird angezeigt). Für ein Multitaper-Spektrum mit einer Fourier-Breite 3 liegt die Dämpfung bei wesentlich höheren 56% (nur 44% der Amplitude wird angezeigt).
Ändern Sie Anzahl der DPSS-Fenster auf 3.
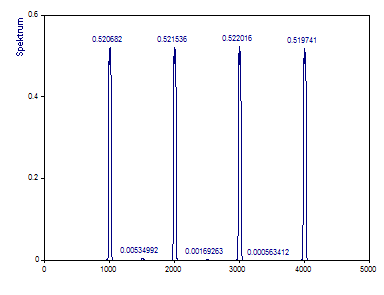
Die Dämpfung ist nicht nur eine Funktion der Fourier-Breite der Multitaper-Analyse, sondern wird ebenfalls entscheidend von der Anzahl der verwendeten Bewertungsfenster beeinflusst. Für den Fall, dass nur die ersten drei Slepian-Bewertungsfenster verwendet werden, liegt die Dämpfung der Amplitude bei ungefähr 48% im Gegensatz zu 56% Dämpfung bei der Maximalanzahl von 5 Bewertungsfenstern.
Die Auswahl der Normierungsart Amplitude kompensiert die Dämpfung perfekt.
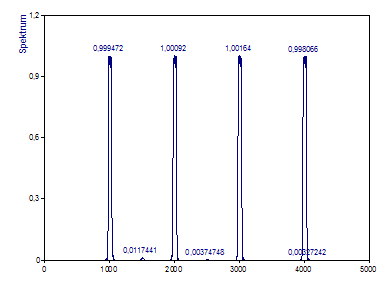
Die beste Methode für eine Fourier-Analyse mit hohen Dynamikbereich und niedriger Varianz
(1) Stellen Sie sicher, dass die Daten weiteren Sinn stationär (WSS = Wide-Sense Stationary) über die volle Länge der Datensätze sind. Verwenden Sie die STFT oder CWT-Analyse um sicherzustellen, dass der Spektralgehalt des Datensatzes nicht von der Zeit abhängt. Ein Bewertungsfenster wird die Informationen an den beiden Enden des Datensatzes bedeutend verringern. Das sollte nur gemacht werden, wenn der Einfluss der Daten an den beiden Rändern des Datensatzes sicher vernachlässigt werden kann.
(2) Um den Leckeffekt zu reduzieren und eine Fourieranalyse mit einem hohen Dynamikbereich zu erzielen, werden im Allgemeinen Bewertungsfenster benötigt. Seien Sie also darauf gefasst, dass die Amplituden und Leistungen des Spektrums gedämpft sind und daher nicht direkt aus den Peaks abgelesen werden können. Um Leistungen und Amplituden exakt auszuwerten, verwenden Sie die Amplitudennormierung.
(3) Falls die Datenlänge sehr groß ist, beginnt die Analyse mit einer hohen Auflösung im Frequenzbereich. Etwas davon kann für eine Varianzreduktion geopfert werden, durch Einsatz der Periodogramm-Methode.
(4) Falls die Datenlänge begrenzt ist und das Ziel der Analyse sowohl die Abschätzung der Frequenz als auch der Leistung ist, kann es nötig sein, das einzelne Fourier-Spektrum zu verwenden. Die Peaks des Spektrum haben zwar die maximal mögliche Auflösung, aber die Varianz ist größer, da mehr durch Rauschen verursachte Peaks vorhanden sind. Die Fourier-Spektralanalyse ist auch die beste Möglichkeit, ein gegebenes Signal vom Rauschen abzugrenzen, da hier kritische Grenzen für alle Bewertungsfenster angeboten werden, während diese beim Periodogramm nur im unbewerteten Fall angezeigt werden können.
(5) Wenn die Datenlänge begrenzt ist und das primäre Ziel der Analyse die Abschätzung der Leistung ist und besonders, wenn alle Informationen der Daten wichtig sind, insbesondere die an den Rändern des Datensatzes, ist das Multitaper-Spektrum die beste Wahl.
(6) Alle drei Analyseverfahren sind auf eine Vielzahl von Spektralanalyse-Problemen anwendbar. FlexPro erleichtert die Auswahl der richtigen Methode, indem alle drei Algorithmen in einer einzigen Analyseoption angeboten werden. Mit Hilfe der Referenz-Funktion lassen sich die unterschiedlichen Prozeduren vergleichen. Manchmal wird das beste Analyseergebnis durch die Anwendung aller drei Methoden erreicht.
Schritt 3 - Ausgabe-Optionen
Um sich die Objekte, die der Analyseassistent automatisch erzeugt, anzusehen, erzeugen Sie ein Fourier-Spektrum.
Als Spektralprozedur wählen Sie Fourier-Spektrum. Als Spektrumtyp wählen Sie dB, normiert. Als Fenstertyp wählen Sie Kaiser-Bessel und als Fensteranpassung geben Sie 3.0 ein. Setzen sie die FFT-Länge auf 8192. Markieren Sie die Maximale Peak-Anzahl-Option und geben Sie einen Wert von 7 ein. Nun setzen Sie Kritische Grenze Weißes Rauschen % auf 99. Klicken Sie auf die Beschriftungen-Schaltfläche, bis die Frequenzbeschriftungen in der Grafik erscheinen. Klicken Sie auf Weiter. Machen Sie in Schritt 3 an alle drei Optionen einen Haken und klicken Sie anschließend auf Fertigstellen.
Acht Objekte wurden in der FlexPro-Projektdatenbank erzeugt.
"Spektrum" ist das Analyseobjekt. Es führt die Spektralanalyse aus. Sie können das Objekt durch einen Doppelklick öffnen.
"Kritische Grenze" ist die Formel zur Erzeugen der kritischen Grenzen, die bei der Darstellung benutzt werden.
"Peaks" ist die Formel zur Erzeugung der Peakinformationen, die bei der Darstellung benutzt werden.
"HarmonischeAnalyse" ist die Formel, die den Bericht der harmonischen Analyse generiert.
Das Diagramm "Spektrum" ist die Darstellung des Fourier-Spektrums, das durch den Analyseassistenten erzeugt wurde. Es verwendet die Objekte "Spektrum", "Kritische Grenze" und "Peaks".
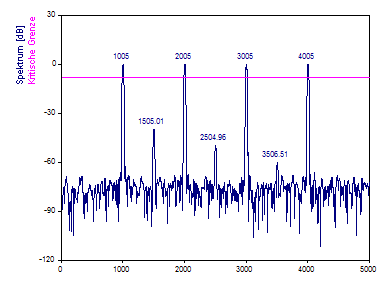
"Daten" ist ein Diagramm der ursprünglichen Daten des Zeitbereichs.
"HarmonischeAnalyse" ist eine Tabelle mit den Spektralinformationen für die sieben Spektralkomponenten, festgelegt durch die maximale Peak-Anzahl von 7. Diese Tabelle zeigt Frequenz, Amplitude, Phase und TISA-Leistung. Bei "% Leistung" liefert die Summe aller Komponenten 100%, die Werte der Spalte "Relativ %" ordnen die 100% der Komponente mit der größten Leistung zu.
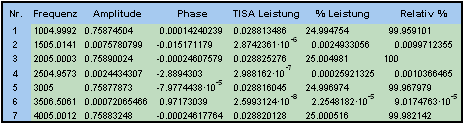
"Fourier" ist ein Dokument, das die Spektren und Diagramme der Daten enthält.
Spektralanalyse für nicht-äquidistant abgetastete Daten
Im Folgenden werden die Möglichkeiten der Fourier-Spektralanalyse nicht-äquidistant abgetasteter Daten in FlexPro behandelt. Das Hauptaugenmerk ist auf eine Fourier-Prozedur gerichtet, die für ungleichmäßig abgetastete Daten ausgelegt ist.
Sie können den Rest dieses Tutorials überspringen, falls Sie immer mit gleichmäßig abgetasteten Werten arbeiten.
Öffnen Sie den Ordner Tutorials in der Beispieldatenbank und darin den Unterordner Fourier Uneven und öffnen Sie das 2D-Diagramm Data per Doppelklick.
Hier sehen Sie die Darstellung des Signals mit 1000 Fließkommawerten. Die X-Werte liegen aufsteigend im Bereich von 0 bis 10, weisen jedoch kein konstantes Abtastinterval auf. Es handelt sich um ein "Worst-Case" Szenario für den Fourier-Algorithmus für nicht-äquidistant abgetastete Daten.
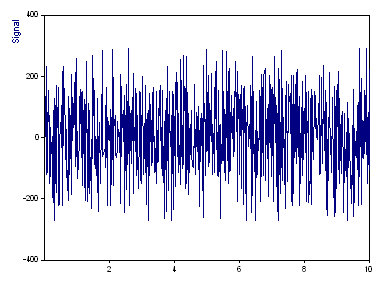
Dieser Datensatz enthält drei Peaks, einen bei der Frequenz 30 (Amplitude 100, Phase 3π/2), ein weiterer bei der Frequenz 70 (Amplitude 100, Phase π), und ein dritter Peak bei der Frequenz 120 (Amplitude 100, Phase π/2). Die sich aus dem Kehrwert der mittleren Abtastrate ergebende durchschnittliche Nyquist-Frequenz ist 50,05. Es liegen also zwei Peaks über dieser Grenze.
Ein wichtiger Unterschied ungleichmäßig abgetasteter Daten gegenüber gleichmäßig abgetasteter Daten ist die Tatsache, dass Informationen über der mittleren Nyquist-Grenze nicht mehr automatisch auf niedrigere Frequenzen gespiegelt ("aliased") werden. Es ist daher möglich, Informationen, die über der Nyquist-Frequenz liegen, zu extrahieren, da einige der Datenwerte näher zusammen liegen und deshalb eine wesentlich höhere "lokale" Nyquist-Frequenz vorliegt.
Dementsprechend gibt es weiter auseinander liegende Punkte, deren lokale Nyquist-Frequenz unter dem Durchschnitt liegt. Daher sind die Informationen innerhalb des durchschnittlichen Nyquist-Bereichs unvollständig.
Lomb-Scargle-Periodogramm
Das Lomb-Scargle-Periodogramm ist ein Algorithmus, der ein Fourier-Spektrum speziell für den Fall erzeugt, bei dem Daten ungleichmäßig verteilt sind.
Schließen Sie das Diagramm und markieren Sie den Datensatz Signal.
Klicken Sie auf Einfügen[Analysen] > Analyse-Assistent. Wählen Sie Analysen für nicht-äquidistant abgetastete Daten in Spektralanalysen und anschließend Fourier-Spektrum, nicht-äquid. Klicken Sie auf Weiter.
In Schritt 2 des Analyseassistenten beginnen Sie mit der Ansicht des unbewerteten Fourier-Spektrums mit einer maximalen Frequenz, die der mittleren Nyquist-Frequenz entspricht.
Als Spektrumtyp wählen Sie dB, normiert. Als Fenstertyp wählen Sie Rechteck -13dB W=1 (keine Fensterung). Frequenzanzahl setzen Sie auf 1024 und Nyquist-Vielfaches setzen Sie auf 1,0. Aktivieren Sie Maximale Peak-Anzahl und geben Sie 3 ein. Kritische Grenze Weißes Rauschen % wird auf 99 gesetzt.
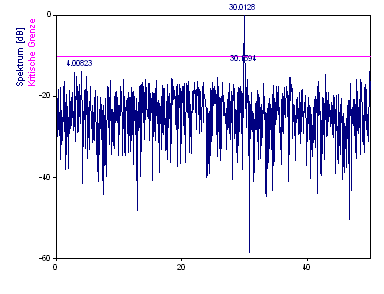
Es wurde nur ein Peak bei Frequenz 30 gefunden, da die Peaks bei Frequenz 70 und 120 über der durchschnittlichen Nyquist-Frequenz liegen.
Der größte Peak ist über der 99 % kritischen Grenze, was bedeutet, dass es eine weniger als ein-prozentige Wahrscheinlichkeit gibt, dass diese größte Spektralkomponente durch Rauschen verursacht wurde. Anders gesagt, bei 100 Datensätzen mit weißem Rauschen mit gleicher Varianz würde bei nicht einem ein Peak dieses Betrages erwartet werden.
Beachten Sie auch, dass dieser Algorithmus keine Spektrallinie für die Frequenz 0 erzeugt.
Erweitern des Spektrums über die durchschnittliche Nyquist-Frequenz hinaus
Ändern Sie Nyquist-Vielfaches auf 2,0. Um die Spektraldichte beizubehalten, vergrößern Sie Frequenzanzahl auf 2048.
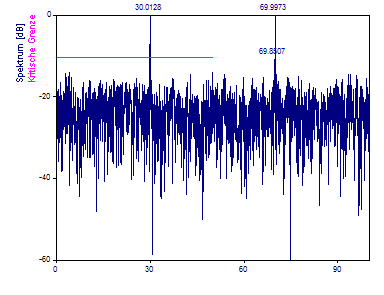
Sie sehen, dass im Spektrum die Frequenzkomponenten 30 und 70 sichtbar sind.
Ändern Sie Nyquist-Vielfaches auf 4,0. Um die Spektraldichte beizubehalten, vergrößern Sie Frequenzanzahl auf 4096.
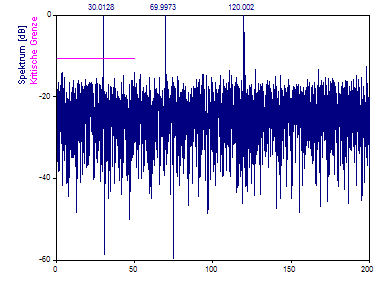
Erweitern Sie das Spektrum auf das Vierfache der mittleren Nyquist-Grenze, so werden alle Komponenten entdeckt, einschließlich dem Peak bei Frequenz 120.
Beachten Sie, dass dieser Algorithmus eine interne Interpolation verwendet, die nicht frei von Fehlern ist. Die Sinuskurven der Daten sind ohne Rauschen angelegt und trotzdem wird ein Hintergrundrauschen von ungefähr -25 dB angezeigt. Dies beschränkt die Einsatzmöglichkeiten dieser Prozedur für eine Fourier-Analyse mit hohem Dynamikbereich.
Bewertungsfenster
FlexPro erweitert den Algorithmus, um Fensterung anzubieten. Es werden alle Fenster angeboten, die auf ungleichmäßig verteilte Zeitwerte angewendet werden können. Die Tschebyscheff- und Slepian(DPSS)-Fenster sind nicht verfügbar, wenngleich ein approximiertes Tschebyscheff-Fenster verfügbar ist, um den schärfst-möglichen Peak für ein gegebenes größtes Nebenmaxima (sidelobe) zu ermitteln.
Ändern Sie Fenstertyp auf Cos3 Minimum Sidelobe -71dB W=3.
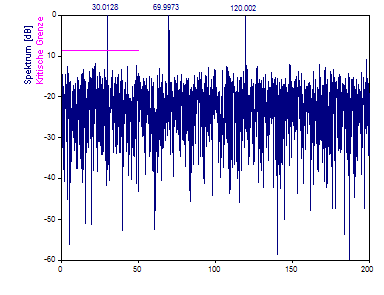
Durch den Interpolationsfehler bringt das Bewertungsfenster nur wenig Verbesserung.
Kritische Grenzen
Das Lomb-Scargle-Periodogramm beinhaltet üblicherweise eine Vertrauensgrenze, die auf der Exponentialverteilung basiert. In FlexPro wird diese nicht verwendet. Stattdessen sind kritische Grenzen verfügbar. Wie bei der Fourier-Analyse für äquidistant abgetastete Daten, werden auch hier spezielle Modelle zur Berechnung der kritischen Grenzen für jedes der angebotenen Bewertungsfenster benutzt. Sie basieren auf aufwendigen Monte-Carlo-Versuchen. Da die Verteilung der Abszissenwerte Einfluss auf die kritischen Grenzen haben kann, sollten die angezeigten kritischen Grenzen als Näherung angesehen werden.
Amplitudendämpfung
Ändern Sie Fenstertyp zu Rechteck -13dB W=1, die Normierung auf Leistung und setzen Sie das Feld Nyquist-Vielfaches auf 3. Wählen Sie Amplitude als Spektrumtyp.
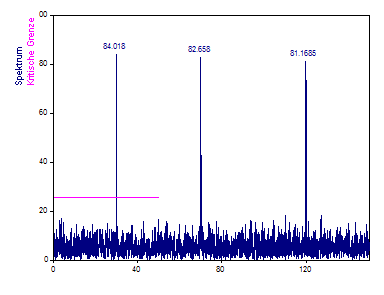
Im Gegensatz zur Fourier-Analyse für äquidistant abgetastete Daten, bei der das Abschalten der Fensterung zur Anzeige fast der tatsächlichen Amplitudenwerte führt, tritt beim Lomb-Scargle-Algorithmus auch in diesem Fall eine Dämpfung auf wenn die Signalenergie im Spektrum erhalten bleiben soll. Die Anwendung von Bewertungsfenstern führt zu einer weiteren Amplituden- und Leistungsdämpfung.
Die Wahl der Normierung Amplitude kompensiert die Dämpfung.
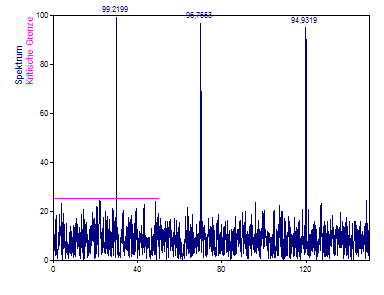
Klicken Sie auf Weiter. Machen Sie in Schritt 3 an alle drei Optionen einen Haken und klicken Sie anschließend auf Fertigstellen.
Es wurden wiederum acht Objekte in der FlexPro-Projektdatenbank erzeugt. Der einzige Unterschied liegt darin, dass die Phase der Spektralkomponenten nicht berechnet wurde, da dies bei diesem Algorithmus nicht möglich ist.
Literatur
Gute Einführungen in die digitale Signalverarbeitung sind:
•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.
•H.D. Lüke (1985). Signalübertragung. Springer-Verlag Berlin, Heidelberg, New York. ISBN 3-540-15526-0.
Die in FlexPro verwendeten FFT-Algorithmen sind hier beschrieben:
•C. Temperton, "Implementation of a Self-Sorting In-Place Prime Factor FFT Algorithm", Journal of Computational Physics, v. 58, p. 283, 1985
•R. C. Singleton, "An Algorithm for Computing the Mixed Radix Fast Fourier Transform", IEEE Trans. Audio Electroacoust., v. AU-17, p. 93, June 1969
•L. R. Rabiner, R. W. Schafer, C. M. Rader, "The Chirp z-Transform Algorithm and Its Application", BSTJ, 48, p.1249, May-June 1969
Informationen über Bewertungsfenster finden Sie in:
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, Feb. 1981.
Information über Multitaper-Spektren können Sie hier nachlesen:
•Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis", Computers and Geosciences, v21, p199, 1995.
Siehe auch
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen