Bewertungsfenster
Bewertungsfenster werden zur Verringerung des Leckeffekts in Fourier-Spektren verwendet.
Bewertungsfenster mit fester Breite
Die folgenden Bewertungsfenster mit fester Breite stehen in FlexPro zur Verfügung. Die Charakterisierung der Fenster erfolgt im Frequenzbereich. Der dB-Wert gibt die Dämpfung des ersten Nebenmaximums (Sidelobe) gegenüber dem Hauptmaximum (Mainlobe) an. Mit wachsender Dämpfung reduziert sich der Leckeffekt. Der Begriff "Rolloff" bezeichnet das Abklingen der Nebenmaxima. Mit wachsendem Rolloff verringert sich die spektrale Streuung des Leckeffekts. Der Wert W (Width) bezeichnet die einseitige Breite des Hauptmaximums als Vielfache der Breite des Hauptmaximums des Rechteckfensters. Mit wachsender Breite verringert sich die spektrale Auflösung.
Fenster |
Wird berechnet mit |
|---|---|
Rechteck -13dB W=1 (Keine Fensterbewertung) |
1.0 |
Welch -21dB W=1,4 |
1.0-(((n-1)-2*i)/(n-1)*((n-1)-2*i)/(n-1)), i=0..n-1 |
Sine -23dB W=1,5 |
sin(π*i/(n-1)), i=0..n-1 |
BiSquare -28dB W=1,8 (Connes) |
1.0-(absolute(i-0.5*n+0.5))²/(0.5*n-0.5)²)², i=0..n-1 |
Bartlett -27dB W=2 |
2*i/(n-1), i=0..(n-1)/2 2-2*i/(n-1), i=(n-1)/2+1..n-1 |
0.5-0.5*cos(2*π*i/(n-1)), i=0..n-1 |
|
TukeyHann -37dB W=2 |
0.25*Dirichlet(2*(i/(n-1))-1.0-0.5)+(1.0-2.0*0.25)*Dirichlet(2*(i/(n-1))-1.0)+0.25*Dirichlet(2*(i/(n-1))-1.0+0.5), i=0..n-1 mit Dirichlet(q)=sin((2*π+0.5)*q)/(2*π*sin(0.5*q)) |
Bartlett modifiziert -39dB W=2,3 |
(sin(π*(2*(i/(n-1))-1)))²/(2*π*sin((i/(n-1))-0.5))², i=0..n-1 |
0.53836-0.46164*cos(2*π*i/(n-1)), i=0..n-1 |
|
Cos3 Maximum Rolloff -47dB W=3 |
0.375-0.5*cos(2*π*i/(n-1))+0.125*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman -58dB W=3 |
0.42-0.5*cos(2*π*i/(n-1))+0.08*cos(4*π*i/(n-1)), i=0..n-1 |
0.44959-0.49364*cos(2*π*i/(n-1))+0.05677*cos(4*π*i/(n-1)), i=0..n-1 |
|
Cos3 Nutall -64dB W=3 |
0.40897-0.5*cos(2*π*i/(n-1))+0.09103*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman Exact -68dB W=3 |
0.42659071367153912296-0.49656061908856405847*cos(2*π*i/(n-1))+0.076848667239896818573*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman-Harris -68dB W=3 |
0.42323-0.49755*cos(2*π*i/(n-1))+0.07922*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Minimum Sidelobe -71dB W=3 |
0.4243801-0.4973406*cos(2*π*i/(n-1))+0.0782793*cos(4*π*i/(n-1)), i=0..n-1 |
Cos4 Maximum Rolloff -61dB W=4 |
0.3125-0.46875*cos(2*π*i/(n-1))+0.1875*cos(4*π*i/(n-1))-0.03125*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Blackman-Harris -74dB W=4 |
0.40217-0.49703*cos(2*π*i/(n-1))+0.09892*cos(4*π*i/(n-1))-0.00188*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -83dB W=4 |
0.338946-0.481973*cos(2*π*i/(n-1))+0.161054*cos(4*π*i/(n-1))-0.018027*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Blackman-Harris -92dB W=4 |
0.35875-0.48829*cos(2*π*i/(n-1))+0.14128*cos(4*π*i/(n-1))-0.01168*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -93dB W=4 |
0.355768-0.487396*cos(2*π*i/(n-1))+0.144232*cos(4*π*i/(n-1))-0.012604*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -96dB W=4 |
0.3635819-0.4891775*cos(2*π*i/(n-1))+0.1365995*cos(4*π*i/(n-1))-0.0106411*cos(6*π*i/(n-1)), i=0..n-1 |
1-1.93*cos(2*π*i/(n-1))+1.29*cos(4*π*i/(n-1))-0.388*cos(6*π*i/(n-1))+0.0322*cos(8*π*i/(n-1)), i=0..n-1 |
Bewertungsfenster mit variabler Breite
Die folgenden Bewertungsfenster mit anpassbarer Breite stehen in FlexPro zur Verfügung:
Fenster |
Wird berechnet mit |
|---|---|
Beta |
4*(1-i/(n-1))*i/(n-1))^(-3.218913776512187+2.760793796409310*a), i=0..n-1 a=Breite des Hauptmaximums |
Cosine Maximum Rolloff |
absolute(0.5*(1-cos(2*π*i/(n-1)))))^(a-1), i=0..n-1 Dies ist das Kosinusfenster mit maximalem Abklingen der Nebenmaxima. |
Kaiser-Bessel |
I0(sqrt((a²-1.0)/0.10132118361)*sqrt(i*(2*((n-1)/2)-i))/((n-1)/2))/I0(sqrt((a²-1.0)/0.10132118361)), i=0..n-1 a=Breite des Hauptmaximums, I0 ist die modifizierte Bessel-Funktion |
van der Maas |
0.5*I1(2*(0.5*π*sqrt(4*a*a-1))*sqrt((i/(n-1))*(1-(i/(n-1)))))/(sqrt((i/(n-1))*(1-(i/(n-1))))*I1(0.5*π*sqrt(4*a*a-1))), i=0..n-1 a=Breite des Hauptmaximums, I1 ist die modifizierte Bessel-Funktion |
Dieses Fenster erzeugt minimalen Leckeffekt durch die Nebenmaxima, hat jedoch keinen "Rolloff". Es wird im Frequenzbereich konstruiert und zur Anwendung im Zeitbereich invers transformiert. FlexPro implementiert das Tschebyscheff Fenster im Bereich von -30dB bis -150dB.
Siehe auch Programm 5.2 in "IEEE Programs for Digital Signal Processing" |
|
Tschebyscheff (approximiert) |
Dies ist eine in FlexPro verwendete Approximation des Tschebyscheff-Fensters mit einem Gültigkeitsbereich von -50 bis -130dB. Es kommt hauptsächlich im Analyseobjekt Fourier-Analyse für nicht-äquidistant abgetastete Daten zum Einsatz. |
Slepian (DPSS) |
Dies ist das erste Fenster aus der Slepian DPSS Reihe. Der Parameter a entspricht ungefähr der Breite des Hauptmaximums.
Siehe auch Jonathan Lees und Jeffrey Park, "Multiple Taper Spectral Analysis" |
Gaussian |
exp(-4*ln(2)*((i-((n-1)/2))/((n-1)*((2.453274901281656+a*0.3202556336455866)/(1.0+a*(2.348619671799226))))²), i=0..n-1 a=Breite des Hauptmaximums |
Cosine Taper |
if(i>(int)(a*n+0.5) and i<(int)((1.0-a)*n-0.5)), 1.0, 0.5-0.5*cos((π/a/(n-1))*(if(i>0.5*n, n-i-1, i)))), i=0..n-1 Das Fenster variiert von Hann bei a=0.5 bis Rechteck für a gegen 0. |
Die folgenden Grafiken zeigen eine Reihe der beliebtesten Fenster:
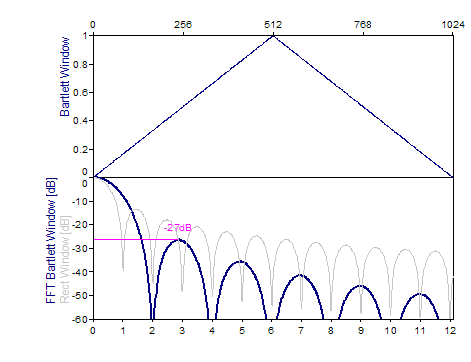
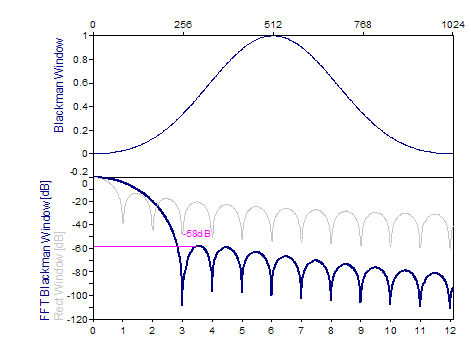
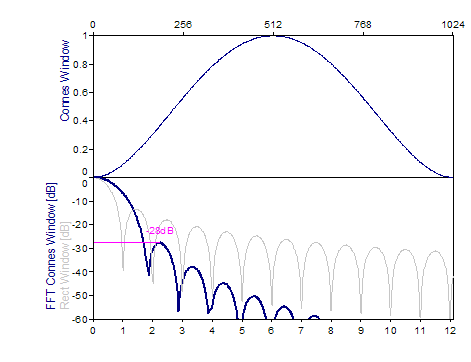
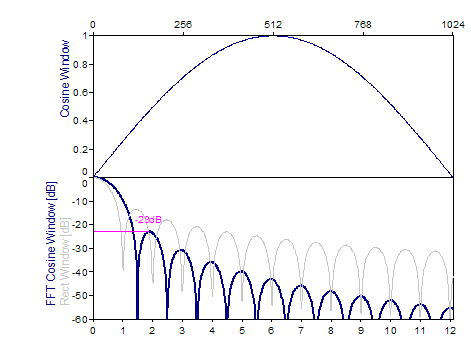
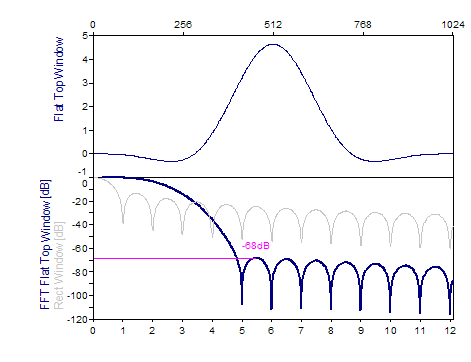
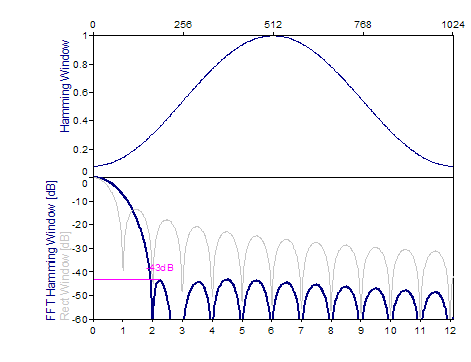
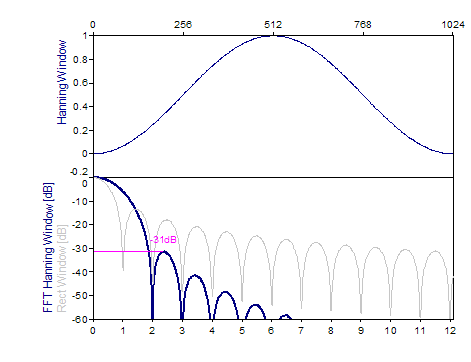
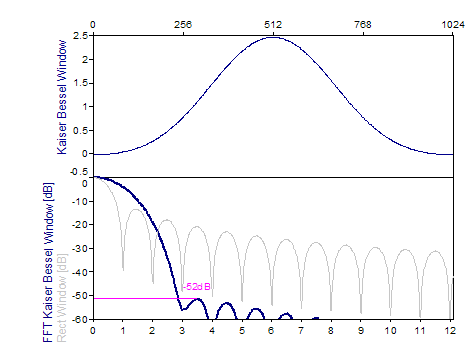
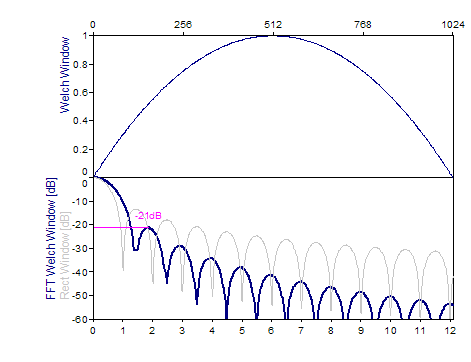
Literatur
Eine Implementierung des Tschebyscheff-Fensters ist beschrieben in:
•IEEE Programs for Digital Signal Processing, IEEE Press, 1979.
Das Slepian (DPSS) Fenster wird vorgestellt in:
•Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis", Computers and Geosciences, v21, p199, 1995.
Ein Überblick über verschiedene Fenster gibt:
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, Feb. 1981.