Tutorial Spektralschätzer
Dieses Tutorial behandelt die Spektralanalysen in FlexPro, die sich auf autoregressive parametrische Modellierung und Eigenwertanalyse beziehen. Diese fortschrittlichen Verfahren eignen sich insbesondere zur Frequenzschätzung kleiner Datensätze.
Frequenzschätzer
Die AR- und ARMA-Spektralschätzer sind Modellierungsprozeduren, die ein Autoregressives (AR) beziehungsweise ein Autoregressive-Moving Average (ARMA) Modell zur Schätzung der Spektren von Zeitreihen verwenden. Die Eigenwertanalyse verwendet Rausch-Eigenmoden, um ein orthogonales Frequenzspektrum zu konstruieren, das nur die schmalbandige Spektralkomponenten des Signals enthält. Alle drei Algorithmen sind Spektralschätzer, d.h. sie bieten eine sehr exakte Schätzung der Frequenzen von vorhanden Harmonischen. Allerdings ist die Schätzung von deren Leistung im Allgemeinen nicht genau.
Extrahieren stationärer Segmente
Da diese Methoden rechenintensiv sind, sind sie am besten für kleine Datensätze sinnvoll, wo die Fourier-Analyse unzureichende Auflösung benötigt. Da außerdem die Signaldaten stationär sein müssen, ist es oft sinnvoll, einen kleinen Bereich des Datensatzes zu extrahieren, in dem das Signal näherungsweise stationär ist, d. h. einen von der Zeit unabhängigen Spektralgehalt aufweist. In diesem Tutorial wird ein Testsignal mit einer kleinen Datenlänge verwendet, das genauso ein Stück aus einem viel größeren Datensatz sein könnte.
Ein geeignetes Testsignal
Für dieses Tutorial wird ein kurzes Datensignal der Länge 64 benutzt, das drei Sinuskurven enthält, die zu nah zusammen liegen, um mit der Fourier-Analyse aufgelöst zu werden.
100.0*sin(2π*x*420+p/2)
50.0*sin(2π*x*500+p)
100.0*sin(2π*x*580+3p/2)
Die Abtastrate beträgt 5000 Hz, die Nyquist-Frequenz, die maximale Frequenz, die ausgewertet werden kann, liegt daher bei 2500 Hz. Alle Schwingungen über dieser Frequenz werden auf niedrigere Frequenzen gespiegelt ("Aliasing"). Die Zeitwerte variieren von 0 bis 0,0126 bei einem Abtastintervall von 0,0002. Es wurde 10% zufälliges Gauß-Rauschen hinzugefügt. Dies bewirkt ein Hintergrundrauschen von ungefähr -30dB relativ zum größten Peak.
Die Amplitude der mittleren Sinuskurve ist halb so groß wie die der beiden anderen Sinuskurven und besitzt ein Viertel der Leistung der beiden anderen Schwingungen. Beachten Sie, dass dies kein Datensatz mit hohem Dynamikbereich ist, sondern einer, bei dem alle drei Peaks signifikante Leistung haben. Der mittlere Peak liegt nur -6 dB unter den beiden anderen Peaks. Daher haben die Optimierungen im Frequenzbereich wenig Auswirkungen auf die Auflösung des mittleren Peaks.
Wählen Sie Datei > Projektdatenbank öffnen und öffnen Sie die Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Tutorials\Spectral Analysis.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021>Examples>Tutorials>Spectral Analysis.fpd. Öffnen Sie den Ordner Tutorials und darin den Unterordner Frequency Estimators und öffnen Sie das 2D-Diagramm Data per Doppelklick.
Dies ist die Darstellung des Signals, das 64 Fließkomma-Werte hat.
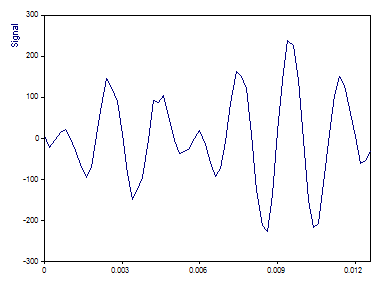
Fourier-Spektrum
Wir werden ein Hamming-Bewertungsfenster einsetzen, welches für die einseitige Breite des Hauptmaximums von 2 eine best-mögliche Dämpfung des ersten Nebenmaximums aufweist.
Schließen das Diagramm und markieren Sie den Datensatz Signal.
Klicken Sie auf Einfügen[Analysen] > Analyse-Assistent.
Wählen Sie die Kategorie Fourier-Analyse unter Spektralanalysen aus. Dort wählen Sie Fourier-Spektrum aus. Klicken Sie auf die Weiter-Schaltfläche.
Beachten Sie, dass als Spektralprozedur Fourier-Spektrum ausgewählt ist. Obwohl die Spektralprozedur schon in Schritt 1 ausgewählt wurde, kann sie in Schritt 2 verändert werden.
Wählen Sie als Spektrumtyp den Wert dB, normiert.
So wird der größte Peak im Spektrum auf 0 dB normiert. Alle anderen Peaks haben dann einen negativen Wert. Ein Peak bei -3 dB hätte halb so viel Energie wie ein Peak bei 0 dB und ein Peak bei -6 dB hätte eine halb so große Amplitude.
Als Fenstertyp wählen Sie Hamming -43dB W=2.
Im Spektralanalyse-Modul werden allen festen nicht einstellbaren Bewertungsfenster durch ihren Namen, die Abschwächung des Nebenmaximums in dB und die einseitige Fourier-Bereichsbreite aufgelistet. Eine Rechteckfensterung entspricht keiner Fensterung, da alle Datenelemente mit Eins multipliziert werden.
Stellen Sie sicher, dass die FFT-Länge auf die Datenlänge bzw. 64 gesetzt wird.
Das Nullen anhängen-Informationsfeld zeigt, dass kein Anhängen von Nullen (zero padding) stattfindet.
Wählen Sie die Maximale Peak-Anzahl Option und geben dort den Wert 3 ein.
Der Analyseassistent erzeugt automatisch Information über die Peaks des Spektrums. Ist die Option auf 3 eingestellt, so werden die drei Peaks mit der größten Leistung angezeigt. Beachten Sie bitte, dass es auch möglich ist, einen dB-Schwellenwert unter dem höchsten Peak anzugeben. Für diesen Datensatz könnten Sie einen -65 dB Schwellenwert einstellen.
Setzen Sie jetzt Kritische Grenze Weißes Rauschen % auf Keine.
Falls über den Peaks keine Beschriftungen sichtbar sind, Klicken Sie auf Beschriftungen, bis die Frequenz-Beschriftungen erscheinen.
Sie können zwischen mehreren Einstellungen wählen. Sie können die Beschriftung für die Y-Komponente des Spektrums (hier in dB, normiert) oder für die X-Komponente (immer Frequenzen) anschalten. Alternativ können Sie die Beschriftungen auch abschalten.
Die Fourier-Grafik im Analyseassistenten sollte folgendermaßen aussehen:
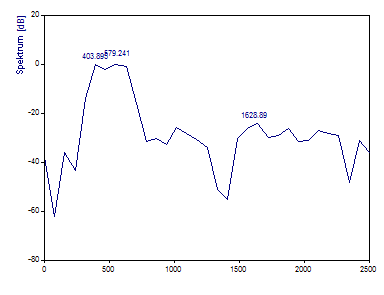
Setzen Sie die FFT-Länge auf 8192.
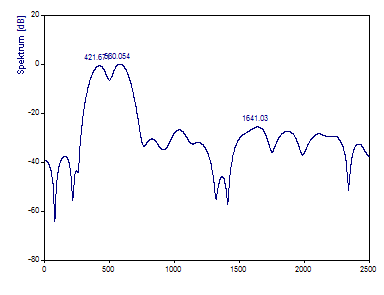
Durch das Anhängen von Nullen werden die Peaks mit der größten Leistung (bei 420 und 580) besser erkannt, aber die Länge der Daten ist zu kurz, um eine Auflösung der Sinuskurve mit der niedrigeren Amplitude und der Frequenz 500 zu erhalten. Es kann nichts getan werden, um die benötigte Auflösung für die Fourier-Analyse für diesen Datensatz herzustellen. Es muss länger abgetastet werden. Jetzt werden Sie sehen, was passiert, wenn der gleiche Datensatz doppelt so lang abgetastet wird.
Klicken Sie auf Abbrechen. Markieren Sie den Datensatz Signal2.
Klicken Sie erneut auf den Analyseassistenten. Wählen Sie die Kategorie Fourier-Analyse unter Spektralanalysen aus. Dort wählen Sie Fourier-Spektrum aus. Klicken Sie auf die Weiter-Schaltfläche. Stellen Sie Spektrumtyp auf dB, normiert, den Fenstertyp auf Hamming -43dB W=2, die FFT-Länge auf 8192, Maximale Peak-Anzahl auf 3, Kritische Grenze Weißes Rauschen % auf Keine. Falls über den Peaks keine Beschriftungen sichtbar sind, klicken Sie auf Beschriftungen, bis die Frequenz-Beschriftungen erscheinen.
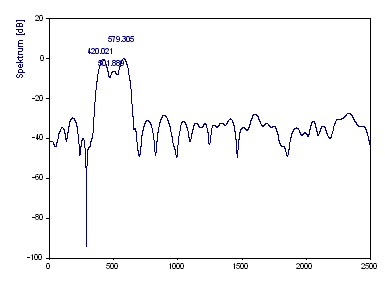
Die 420 Hz Komponente wird bei 420,02 entdeckt, die 500 Hz Komponente bei 501,89 und die 580 Hz Komponente bei 579,30. Der dritte Peak hat die höchste Leistung und ist daher 0 dB. Der erste Peak liegt bei -0,21 dB, der mittlere Peak bei -6,20 dB.
Bei dieser Datensatzlänge ist die Auflösung ausreichend für die Ermittlung der drei Komponenten. Beachten Sie, dass die Genauigkeit sowohl der Frequenz- als auch der Leistungsschätzung sehr gut ist, obwohl Sie sich an der Grenze der Auflösung befinden. Das Ziel dieser Übung war es, zu zeigen, dass es vorteilhaft ist, die Einsatzmöglichkeit der Fourier-Analyse genau zu prüfen, bevor alternative Prozeduren in Erwägung gezogen werden sollten.
Was jedoch, wenn es nicht möglich ist, mehr Informationen durch eine längere Abtastung zu gewinnen? Falls die Daten einen näherungsweise stationären Schnappschuss eines sich schnell verändernden Signals darstellen, ist es nicht möglich, die Frequenzauflösung durch eine längere Abtastung zu erhöhen. In solchen Fällen werden AR-, ARMA- und Eigenwertanalyse-Prozeduren benötigt.
AR-Spektralschätzung
Die Spektralschätzungsmethoden, die im Folgenden vorgestellt werden, sind leistungsstarke Verfahren, wenn die Datenlänge für eine hinreichende Fourier-Analyse zu kurz ist.
Klicken Sie auf Abbrechen. Markieren Sie den ursprünglich verwendeten Datensatz Signal. Er besitzt 64 Werte.
Klicken erneut auf den Analyseassistenten. Wählen Sie die Kategorie Spektralschätzer unter Spektralanalysen aus. Dort wählen Sie AR-Spektralschätzer aus. Klicken Sie auf die Weiter-Schaltfläche.
Wählen Sie den Algorithmus Datenmatrix VR SVD.
Die Prozeduren Autokorrelation, Burg, Normalengleichungen VR und Datenmatrix VR bieten keine integrierte Trennung von Signal und Rauschen. Diese werden in FlexPro zu Vergleichszwecken angeboten und weil diese Verfahren traditionell für AR-Analysen eingesetzt wurden. Diese Prozeduren können Stör-Peaks, gesplittete Peaks und weitere Anomalien erzeugen, die das Analyseergebnis verfälschen können. Daher werden nur die beiden Algorithmen Normalengleichungen VR SVD und Datenmatrix VR SVD empfohlen.
Die Prozedur Normalengleichungen VR SVD kann verwendet werden, um die Berechnungsdauer zu verkürzen. Sie ist bei längeren Datensätzen wesentlich schneller als die Datenmatrix VR SVD-Prozedur.
Setzen Sie den Spektrumtyp auf dB, die Ordnung auf 40 und den Signal-Unterraum auf 6.
Die Ordnung von 40 bedeutet, dass ein AR-Modell mit 40 Koeffizienten aufgestellt wird. Der Signal-Unterraum von 6 gibt vor, dass nur 6 Eigenmoden als dem Signal zugehörig behandelt werden sollen. Die anderen 34 Eigenmoden werden als Rauschen betrachtet und bei der SVD-Berechnung der AR-Koeffizienten unterdrückt. Diese integrierte Trennung von Signal und Rauschen beseitigt den Einfluss von Rauschen auf das Spektrum.
Beachten Sie, dass Sie für jede weitere Spektralkomponente den Signalunterraum um 2 erhöhen müssen. Um z. B. drei Spektralkomponenten abzubilden, muss der Signal-Unterraum auf das Doppelte, also 6, gesetzt werden. Beachten Sie auch, dass bei diesen Prozeduren keine maximale Peak-Anzahl für die Beschriftung der Peaks im Spektrum angegeben werden muss. Für die Nicht-SVD Algorithmen ergibt sich diese Anzahl aus der Anzahl der Wurzeln des AR-Polynoms und für die Algorithmen mit SVD aus der Größe des Signal-Unterraums.
Markieren Sie die Option Adaptive Schrittweite.
Die Option Adaptive Schrittweite erzeugt ein Spektrum mit adaptiver Schrittweite, welches sich über den vollen Nyquist-Bereich erstreckt. Die Frequenzwerte liegen dann im Bereich scharfer Peaks eng zusammen und an den Stellen, an denen die Spektralamplitude geringeren Änderungen unterliegt, weiter auseinander.
Falls über den Peaks keine Beschriftungen sichtbar sind, klicken Sie auf Beschriftungen, bis die Frequenz-Beschriftungen erscheinen.
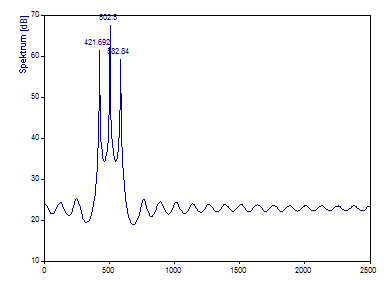
Während die dazwischen liegenden Harmonischen mit der Fourier-Analyse nicht ermittelt werden können, kann eine gut eingestellte AR-Spektralanalyse die drei Spektralkomponenten klar auflösen. Die sehr scharfen Peaks sind typisch für die Harmonischen in einem AR-Spektrum.
Die 420 Hz Komponente wird auf 421,69 geschätzt, die 500 Hz Komponente auf 502,5 und die 580 Hz Komponente auf 582,84. Obwohl der Vergleich mit den Fourier-Spektren der gleichen Daten (mit 64 Punkten) beeindruckend ist, würde die Fourier-Analyse bei einer Datenlänge 128 eine genauere Frequenzschätzung liefern. Beachten Sie auch, dass die Beträge der AR-Peaks dem Leistungs- oder Amplitudenprofil entgegengesetzt sind. Die mittlere Komponente hat den höchsten Betrag im Spektrum. Deshalb sollte die AR-Methode in erster Linie nur als Frequenzschätzer betrachtet werden. Die zweistufige Prozedur der Harmonischen Analyse sollte dazu verwendet werden, Amplituden und Leistungen der Komponenten abzuschätzen.
Wählen Sie nun den Algorithmus Datenmatrix VR.
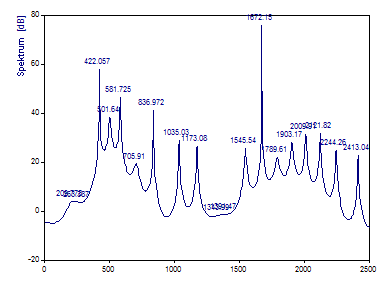
Dies zeigt, was die konventionelle AR-Spektralanalyse historisch als Ergebnis geliefert hatte und warum diese eine geringe Anerkennung erlangt hat. Solange keine integrierte Trennung von Signal und Rauschen zum Einsatz kommt, produziert ein AR-Modell üblicherweise halb so viele Peaks wie bei der Modellordnung angegeben, und es ist nicht ungewöhnlich, dass einige von ihnen verfälscht sind. Ein Rausch-Peak wird sogar mit einem Betrag angezeigt, der größer ist als der eines der relevanten Peaks.
Wählen Sie die Autokorrelation-Methode.
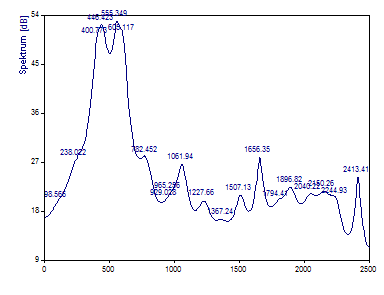
Weil die AR Filter dieser Prozedur immer stabil sind (die komplexen Wurzeln des AR-Polynom liegen immer in oder auf dem Einheitskreis), erscheinen die störenden Peaks des anderen gewöhnlichen AR-Algorithmus ohne Singulärwertzerlegung seltener. Aber diese Methode hat eine deutlich schlechtere Frequenzauflösung. Sie sehen, dass diese AR-Methode nicht geeignet ist, um die mittlere Komponente zu ermitteln.
Eigenwertanalyse-Spektren
Die Methoden der Eigenwertanalyse werden im Allgemeinen als die beste Klasse der Spektralschätzer eingestuft. Die MUSIC (Multiple Signal Classification) und EV (EigenVector) Algorithmen sind für die Schätzung schmalbandiger Komponenten in einem Signal weit verbreitet.
Wählen Sie die Spektralprozedur Eigenwert (MUSIC, EV) und als Algorithmus MUSIC. Stellen Sie sicher, dass der Spektrumtyp auf dB gesetzt ist, die Ordnung auf 40 steht und Signal-Unterraum den Wert 6 hat. Behalten Sie die Option Adaptive Schrittweite bei.
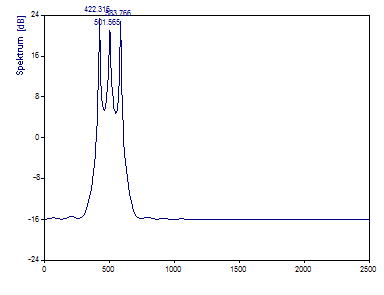
Die 420 Hz Komponente wird auf 422,32 geschätzt, die 500 Hz Komponente auf 501,56 und die 580 Hz Komponente auf 583,77. Obwohl der Vergleich mit den Fourier-Spektren der gleichen Daten (mit 64 Punkten) beeindruckend ist, würde die Fourier-Analyse bei einer Datenlänge 128 auch hier eine genauere Frequenzschätzung liefern.
Des Weiteren sind diese Schätzungen nicht so exakt wie die AR-Prozedur. Die mittlere Komponente hat hier einen niedrigeren Betrag. Obwohl das Profil hier stimmt, sollte die Eigenwertanalyse nur als Frequenzschätzer betrachtet werden. Die zweistufige Prozedur der Harmonischen Analyse sollte dazu verwendet werden, Amplituden und Leistungen der Komponenten abzuschätzen.
Wählen Sie den Algorithmus EV (EigenVector).
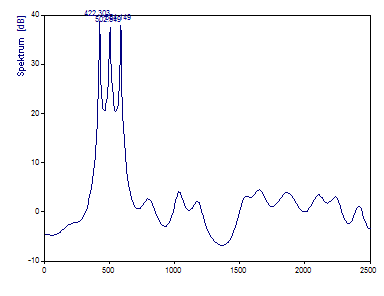
Die 420 Hz Komponente wird auf 422,30 Hz geschätzt, die 500 Hz Komponente auf 502,55 und die 580 Hz Komponente auf 584,14. Für diese Daten war die MUSIC-Prozedur etwas besser in der Abschätzung der Frequenzen.
Bei diesen Prozeduren werden Rausch-Eigenmoden für die Erzeugung der Signalspektren verwendet. Es sollte daher immer eine hohe Anzahl an Rausch-Eigenmoden geben, um das Rauschen im Signal ausreichend abzubilden. Der einzige Unterschied zwischen den Algorithmen MUSIC und EV ist die Gewichtung der Rausch-Eigenmoden.
Harmonische Analyse
Sie werden jetzt eine zweistufige harmonische Analyse durchführen, um die Amplituden und Leistungen der Spektren zu ermitteln.
Klicken Sie auf die Zurück-Schaltfläche. Wählen Sie die Harmonische Analysen und anschließend Harmonische Schätzung. Klicken Sie auf Weiter.
Wählen Sie den AR Datenmatrix VR SVD-Algorithmus, setzen Sie die Komponentenanzahl auf Als maximale Anzahl, die Maximalanzahl auf 3 und den Spektrumtyp auf Harmonische Komponenten. Setzen Sie die Ordnung auf 32.
In dieser zweistufigen Prozedur muss eine niedrige Ordnung gewählt werden. Anomalien können auftreten, wenn die Modellordnung über der halben Datensatzlänge liegt. Um sich gegen diese Effekte abzusichern, die bei diesem automatisierten zweistufigen Algorithmus nicht leicht übersehen werden können, begrenzt FlexPro die Modellordnungen im Harmonischen Spektrum automatisch auf die halbe Datensatzlänge.
Klicken Sie auf Beschriftungen, bis die Amplituden-Beschriftungen erscheinen.
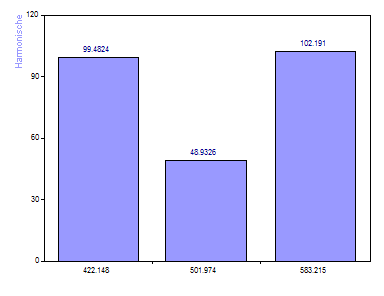
Sie sehen, das die [100, 50, 100] Amplituden bis auf wenige Prozent genau ermittelt wurden.
Klicken Sie auf Weiter. Wählen Sie alle Objekte in Schritt 3. Klicken Sie auf Beenden.
Doppelklicken Sie auf das Objekt HarmonischeAnalyse in der Objektliste von FlexPro.

Die Phasen, die im ursprünglichen Signal verwendet wurden, sind π/2, π, 3π/2. Es ist typisch, dass die kleinsten Fehler bei den Frequenzen auftreten und die größten Fehler bei den Phasen. Hier ist die 1,57 Phase 1,49, die 3,14 Phase ist 2,94 und die 4,71 Phase ist 4,58. Das sind noch sehr gute Werte, wenn man bedenkt, dass dem Testsignal volle 10% Rauschen hinzugefügt wurde.
Literatur
Eine exzellente Darstellung der AR-Spektralalgorithmen finden Sie in:
•S. Lawrence Marple, Jr., "Digital Spectral Analysis with Applications", Prentice-Hall, 1987, p.172-284.
•Steven M. Kay, "Modern Spectral Estimation", Prentice Hall, 1988, p.153-270.
Eine Implementierung des Burg-Algorithmus enthält:
•W. H. Press, et. al, "Numerical Recipes in C", Cambridge University Press, 1992, p.564-575.
Eine gute Darstellung der Eigenwertanalyse-Spektralalgorithmen finden Sie in:
•S. Lawrence Marple, Jr., "Digital Spectral Analysis with Applications", Prentice-Hall, 1987, p.361-378.
•Steven M. Kay, "Modern Spectral Estimation", Prentice Hall, 1988, p.429-434.
Siehe auch
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen