Tutorial Kreuzspektralanalyse
Dieses Tutorial behandelt die Spektralprozeduren in FlexPro, bei denen die Ähnlichkeit zweier Signale analysiert wird. Das Kreuzspektrum, das Kreuzperiodogramm und die Kohärenz-Funktionen bieten Möglichkeiten, die Ähnlichkeit bzw. die Unähnlichkeit zweier Signale zu beurteilen. Diese Verfahren werden oft für Signale angewandt, die aus derselben Quelle stammen. Das muss aber nicht so sein. Es können zwei beliebige Signale derselben Datensatzlänge verwendet werden.
Dieses Tutorial behandelt außerdem die Fourier-Übertrangsfunktionen zwischen einem Eingangs- und einem Ausgangssignal.
Fourier-Analyse
Falls Sie das Fourier-Analyse-Tutorial noch nicht durchgearbeitet haben, sollten Sie dies tun, bevor Sie mit diesem beginnen. Die meisten Prinzipien der Fourier-Analyse sind dort beschrieben. Dieses Tutorial behandelt vorwiegend die Besonderheiten, die bei der Auswertung zweier Signale mittels Kreuzspektralanalyse zu beachten sind.
Zwei Testsignale
Für dieses Tutorial werden zwei Signale der Länge 1024 verwendet. Das erste Signal ist das Referenzsignal, das neun gleichmäßig verteilte Sinuskurven im Nyquist-Bereich enthält:
100.0*sin(2π*x*250+p)
100.0*sin(2π*x*500+p)
100.0*sin(2π*x*750+p)
100.0*sin(2π*x*1000+p)
100.0*sin(2π*x*1250+p)
100.0*sin(2π*x*1500+p)
100.0*sin(2π*x*1750+p)
100.0*sin(2π*x*2000+p)
100.0*sin(2π*x*2250+p)
Um zu sehen, welche Auswirkungen das Verändern der Amplituden, der Frequenzen und der Phasen bei der Kreuzspektralanalyse hat, werden die Komponenten für das zweite Signal wie folgt modifiziert:
100.0*sin(2π*x*250+p)
75.0*sin(2π*x*500+p)
50.0*sin(2π*x*750+p)
25.0*sin(2π*x*1000+p)
0.0*sin(2π*x*1250+p)
100.0*sin(2π*x*1502.5+p)
100.0*sin(2π*x*1775+p)
100.0*sin(2π*x*2000+0)
100.0*sin(2π*x*2250+p/2)
Die ersten fünf Komponenten haben einen linearen Abfall der Amplitude von 100% auf 0%. Die beiden nächsten Komponenten weichen nach oben hin um 0,1% und 1% des Nyquist-Bereichs ab. Die beiden letzten Komponenten haben eine Phasenverschiebung von -p und -p/2.
Die Abtastrate beträgt 5000 Hz. Somit ist die Nyquist-Frequenz, die maximale Frequenz, die ausgewertet werden kann, 2500 Hz. Die Zeitwerte variieren von 0 bis 0,2045 bei einem Abtastintervall von 0,0002. Beiden Signalen wurden 10% zufälliges Gauß-Rauschen hinzugefügt. Dies erzeugt ein Hintergrundrauschen von -40dB relativ zum größten Peak.
Wählen Sie Datei > Projektdatenbank öffnen und öffnen Sie die Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Tutorials\Spectral Analysis.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021>Examples\Tutorials\Spectral Analysis.fpd. Öffnen Sie den Ordner Tutorials und darin den Unterordner Cross Spectral Analysis und öffnen Sie das 2D-Diagramm Data per Doppelklick.
Es handelt sich um ein Diagramm für beide Signale mit jeweils 1024 Fließkomma-Werten.
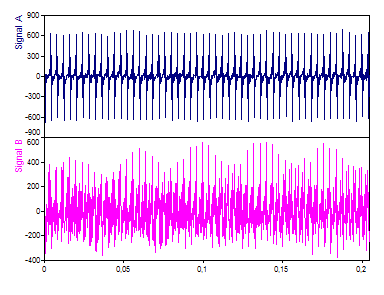
Im Zeitbereich kann man lediglich erkennen, dass es sowohl bedeutsame Gemeinsamkeiten als auch bedeutsame Unterschiede gibt.
Fourier-Spektren
Schließen Sie das Diagramm und markieren Sie den Datensatz Signal A, das Referenzsignal.
Klicken Sie auf Einfügen[Analysen] > Analyse-Assistent.
Wählen Sie die Kategorie Spektralanalysen und darin Fourier-Analysen aus. Dort wählen Sie Fourier-Spektrum aus. Bitte beachten Sie, dass das Ergebnis einiger Spektralprozeduren von der Reihenfolge der markierten Datensätze abhängt. Deshalb sollten Sie immer sorgfältig prüfen, ob die in der Liste mit dem Titel "3) Datensätze zuordnen" angezeigte Zuordnung korrekt ist. Wenn die Reihenfolge nicht stimmt, markieren Sie einen Eintrag und verschieben Sie diesen nach oben oder unten, indem Sie auf die Pfeil-Schaltflächen über der Liste klicken. In unserem Beispiel sollte Signal A der erste Eintrag sein. Klicken Sie danach auf die Weiter Schaltfläche.
Als Spektrumtyp wählen Sie Amplitude. Als Fenstertyp wählen Sie Cos3 Minimum Sidelobe -71dB W=3. Stellen Sie sicher, dass die FFT-Länge auf die Datenlänge oder 1024 gesetzt wird. Wählen Sie Maximale Peak-Anzahl unter Optionen und geben dort den Wert 9 ein. Setzen Sie anschließend Kritische Grenze Weißes Rauschen % auf Keine. Falls über den Peaks keine Beschriftungen sichtbar sind, Klicken Sie auf Beschriftungen, bis die Amplituden-Beschriftungen erscheinen.
Die grafische Darstellung des Fourier-Spektrum im Analyseassistenten sollte folgendermaßen aussehen:
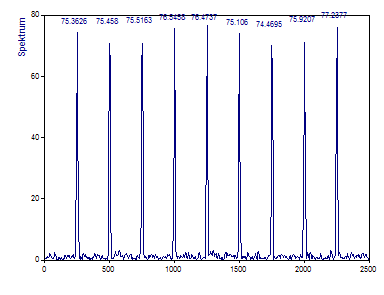
Typischerweise sind die Peaks weder auf den Fourier-Kanälen zentriert, noch ist der Abstand der Oberwellen von der Mitte der Kanäle konstant. Wenn der Abstand am kleinsten ist, sind die Amplituden am größten. Beachten Sie auch, dass die Fensterbewertung dazu führt, dass ein Teil der Spektralinformation auf benachbarte Kanäle verteilt wird. Aus diesem Grund sind die angezeigten Amplituden der Peaks nur ungefähr 75% der tatsächlichen Amplituden der Oberwellen.
Klicken Sie auf Abbrechen und wiederholen Sie die gleichen Schritte für den Datensatz Signal B.
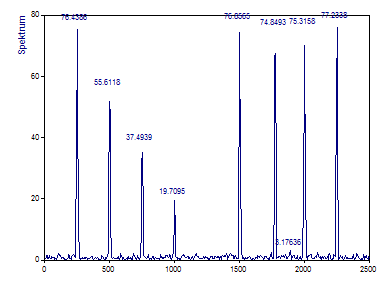
Der einzige ersichtliche Unterschied des zweiten Spektrums sind die verringerten Amplituden gegenüber den ursprünglichen Spektralkomponenten. Schwerer zu erkennen ist die Veränderung in der Frequenz der sechsten und siebten Komponente.
Fourier-Kreuzspektren
Klicken Sie auf Abbrechen, um den Assistenten zu verlassen. Markieren Sie die beiden Datensätze Signal A und Signal B, indem Sie die STRG-Taste während dem Markieren gedrückt halten.
Klicken Sie auf Einfügen[Analysen] > Analyse-Assistent.
Wählen Sie die Kategorie Spektralanalysen und darin Spektralprozeduren für zwei Signale aus. Dort wählen Sie Fourier-Kreuzspektrum aus. Klicken Sie auf die Weiter Schaltfläche.
Wählen Sie wie bei der Fourier-Analyse für den Spektrumtyp die Option Amplitude aus. Wählen Sie für Fenstertyp den Wert Cos 3 Minimum Sidelobe -71dB W=3 aus. Stellen Sie sicher, dass die FFT-Länge auf die Datenlänge oder 1024 gesetzt wird. Wählen Sie Maximale Peak-Anzahl unter Optionen und geben dort den Wert 9 ein. Falls über den Peaks keine Beschriftungen sichtbar sind, klicken Sie auf Beschriftungen, bis die Amplituden-Beschriftungen erscheinen.
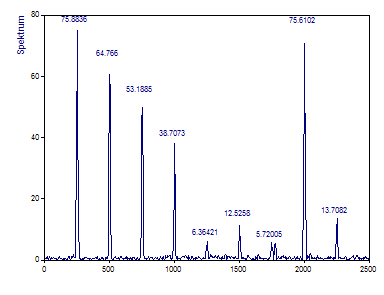
Wenn nur die Amplituden variieren, wie es in der zweiten bis zur vierten Komponente der Fall ist, liegen die Kreuzspektral-Amplituden zwischen denen der beiden Spektren.
An der fünften Position tritt eine Oberschwingung nur in einem der beiden Signale auf. Es tritt hier trotzdem ein kleiner Peak auf. Es handelt sich dabei um das Kreuzspektrum zwischen der leistungsstarken Signalkomponente des Referenzsignals und dem Rauschen im zweiten Signal bei dieser Frequenz. Beachten Sie, dass aus der Existenz eines Peaks bei einer gegebenen Frequenz nicht geschlossen werden kann, dass in beiden Signalen Oberwellen vorhanden sind. In diesem Beispiel gibt es nur im ersten der beiden Signale eine Spektralkomponente bei dieser Frequenz.
An der sechsten Position sehen Sie die Auswirkungen, wenn zwei Peaks um nur 0,1 % des Nyquist-Bereichs von einander abweichen. Es gibt zwar noch einen Kreuzspektrumsanteil, der jedoch gering ist. Es liegt hier eine Verschiebung von nur 2,5 Hz in einem Spektrum vor, das 2500 Hz abdeckt.
An der siebten Stelle weicht die Frequenz um 1% des Nyquist-Bereichs ab, d.h. 25 Hz in diesem Beispiel. Es treten nun zwei Kreuzspektrumsanteile auf, eine bei der Mittenfrequenz des ersten Signals und die andere bei der Mittenfrequenz des zweiten Signals. Die Peaks werden durch das Rauschen verursacht, da es hier keine relevanten Kreuzspektralinhalte gibt.
Wenn die Phase um π abweicht, wie bei der achten Komponente, handelt es sich um den gleichen Unterschied wie bei einem Vergleich zwischen Sinus- und Kosinus-Signalen. Es bleibt die volle Amplitude erhalten. Bei der ungünstigsten Phasenverschiebung π/2, wie bei der neunten Komponente, geht dagegen viel von der Kreuzspektral-Amplitude verloren.
Kreuzperiodogramm
Für das Kreuzperiodogramm gelten die gleichen Prinzipien wie für das Periodogramm, welches die individuellen überlappenden Segmente mittelt, um eine Fourier-Schätzung mit reduzierter Varianz auf Kosten der spektralen Auflösung zu erzeugen.
Wählen Sie den Cross-Periodogramm Algorithmus. Stellen Sie sicher, dass Amplitude ausgewählt ist und der Fenstertyp auf Cos 3 Minimum Sidelobe -71dB W=3 gestellt wird. Die Segmentlänge beträgt Datenlänge/4 oder 256 und die FFT-Länge wird auf Segmentlänge oder 256 gesetzt. Die Überlappung sollte 50% betragen. Wählen Sie Maximale Peak-Anzahl unter Optionen und geben dort den Wert 9 ein. Falls über den Peaks keine Beschriftungen sichtbar sind, klicken Sie auf Beschriftungen, bis die Amplituden-Beschriftungen erscheinen.
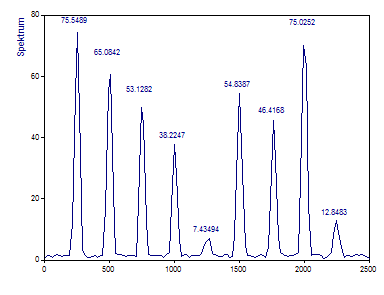
Die Peaks sind breiter, weil die spektrale Auflösung nur ein Viertel des Einzelsegment-Kreuzspektrums beträgt. Diese verminderte Frequenzauflösung ist ein bedeutsamer Faktor in diesem Beispiel.
Die verminderte Varianz führt zu einem deutlich glatteren Spektrum. Die Kreuzspektral-Amplituden der Eingangsgrößen werden exakter bestimmt. Das Kreuzspektrum zwischen der Oberwelle und dem Rauschen an der fünften Frequenzposition ist jetzt ein glatter Peak mit niedriger Leistung.
Der größte Unterschied ist bei der sechsten und siebten Komponente erkennbar. Wegen der verringerten Frequenzauflösung gibt es jetzt eine deutliche Überlappung der Komponenten. Das Ergebnis der 2,5 Hz Verschiebung ist eine Kreuzspektrums-Amplitude, die um weniger als ein drittel reduziert ist. Sogar die 25 Hz Verschiebung resultiert in einer Reduktion der Kreuzspektrums-Amplitude um weniger als der Hälfte der Amplitude, die bei vollständig identischen Frequenzen erzeugt worden wäre.
Die nächsten Schritte werden die Auflösung des Kreuzperiodogramms verbessern. Da wir keine Kreisspektralanalyse mit hohem Dynamikbereich durchführen (d. h. keine Suche nach Spektralkomponenten mit sehr geringer Leistung), werden wir ein Bewertungsfenster verwenden, das nicht so viele Auflösungsverluste im Frequenzbereich verursacht. Die Auflösung wird auch dadurch verdoppelt, dass wir ein Segment benutzen, das halb so groß wie die Datensatzlänge ist. Um die Varianz zu verbessern oder zumindest ein glatteres Spektrum zu erzeugen, wird eine höhere Anzahl von Segmenten durch Vergrößern der Überlappung gemittelt.
Setzen Sie den Fenstertyp auf Cos2 Hanning -31dB W=2 , die Segmentlänge auf 512, die FFT-Länge auf die Segmentlänge oder 512. Verändern Sie die Überlappung auf 90%.
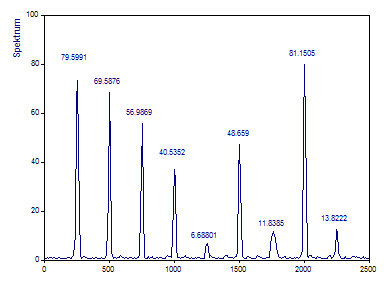
Beachten Sie, dass die Peaks schärfer sind und dass die Amplitude der Kreuzspektral-Peaks für die sechste und siebte Komponente, für welche sich die Ursprungskomponenten in der Frequenz unterscheiden, kleiner geworden ist. Das Spektrum ist etwas weniger glatt aber die Amplituden sind jetzt etwas höher wegen des geringeren Überlaufs in benachbarte Spektrallinien.
Kohärenz
Wenn mehrere Segmente verwendet werden, kann ein Kohärenz-Spektrum erzeugt werden. Die Kohärenz ist 1, wenn es bei einer gegebenen Frequenz Ähnlichkeit der Komponenten gibt und 0, wenn die Signale verschieden bzw. vollständig unkorreliert sind. Dies ist ein übliches Verfahren, um nach Bereichen in einem Spektrum zu suchen, in denen ein Ausgangssignal inkohärent ist, d.h. die Spektralkomponenten keinen Bezug zum Eingangssignal haben.
Wählen Sie die Kohärenz-Prozedur und den Spektraltyp Kohärenz. Lassen Sie alle Einstellungen des Kreuzperiodogramm-Beispiels stehen. Klicken Sie auf die Beschriftungen-Schaltfläche, um die Beschriftungen der Peaks auszuschalten.
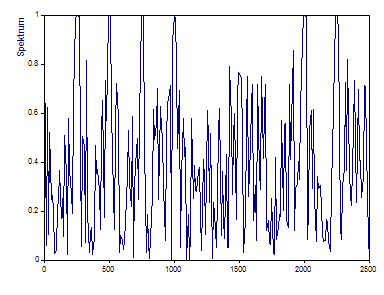
Obwohl die Eingangsgrößen der beiden Signale sich in der Amplitude unterscheiden, hat dies keinen Einfluss auf die MSC (Magnitude-Squared Coherence). Die ersten vier angezeigten Komponenten haben eine Kohärenz, die 1 erreicht.
Die fünfte Komponente, die nur in einem Signal präsent ist, zeigt nichts über der Grundlinie an.
Die Komponenten an der sechsten Stelle, die sich durch nur 2,5 Hz Frequenzunterschied zwischen beiden Signalen auszeichnen, besitzen eine höhere Kohärenz als die Komponenten an der siebten Stelle mit einem Frequenzunterschied von 25 Hz. Beachten Sie also, dass diese siebte Komponente eine gleichmäßig niedrige Kohärenz produziert.
Die MSC ist außerdem phasenunabhängig. Die Komponenten an achter und neunter Stelle erzeugen trotz Phasenverschiebung die Kohärenz 1.
Signal-Rausch-Verhältnis-Spektrum
Wenn mehrere Segmente verwendet werden, ist es auch möglich, ein Signal-Rausch-Verhältnis-Spektrum zu erzeugen. Dieses verwendet die Kohärenz-Werte zum Abschätzen der Signal-Rausch-Verhältnisse jeder Frequenz im Spektrum.
Als Spektrumstyp wählen Sie hierzu Signal-Rausch-Verhältnis dB.
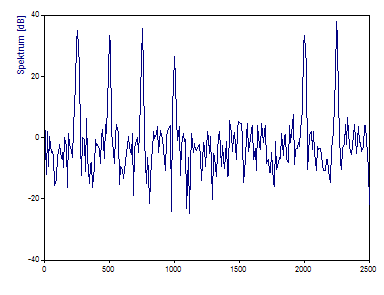
Rufen Sie sich das Hintergrundrauschen von näherungsweise -40dB bei beiden Signalen in Erinnerung. Hier sehen Sie Peaks, die sich ungefähr 40 dB über dem Hintergrundrauschen erheben. Wie bei der Kohärenz zeigen die Komponenten mit sich verändernder Amplitude und sich verändernder Phase vollständigen bzw. fast vollständigen Signal-Rausch-Abstand. Die um 2,5 Hz in der Frequenz abweichenden Komponenten bewirken noch eine leichte Erhöhung des Signal-Rausch-Verhältnisses. Die um 25 Hz abweichenden Komponenten sind dagegen nicht mehr vom Rauschen zu unterscheiden.
Übertragungsfunktion
Die Fourier-Übertragungsfunktion stellt die Übertragungseigenschaften eines Systems im Frequenzbereich dar. In diesem Beispiel enthält das zweite Signal bei allen Frequenzen immer genauso viel bzw. weniger Leistung außer für die beiden Fälle, bei denen es Frequenzverschiebungen gibt.
Im Gegensatz zur Kohärenz und den Signal-Rausch-Verhältnis-Spektren, kann eine Übertragungsfunktion von einem einzelnen Segment berechnet werden. Deshalb werden die gleichen Einstellungen wie beim Beispiel des Kreuzspektrums verwendet.
Wählen Sie die Übertragungsfunktion und den Spektrumstyp dB. Wählen Sie als Fenstertyp Cos 3 Minimum Sidelobe -71dB W=3. Setzen Sie die FFT-Länge auf Datensatzlänge oder 1024. Schalten Sie die Beschriftungen der Peaks aus. Klicken Sie auf das obere Diagramm und anschließend auf das Symbol Cursor aktivieren (das erste in der Symbolleiste unter den Diagrammen).
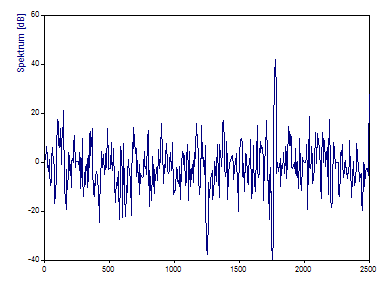
Setzen Sie den Cursor auf 250 Hz, der Position der ersten Komponente. Der Wert ist ungefähr 0,17 bis 0,18 dB. Das Setzen des Cursors auf 500, 750 und 1000 sollte zu den Werten -2,5dB, -6,0dB und -11,7dB führen.
Diese Werte entsprechen der Reduktion der Amplitude im zweiten Signal um 1/4, 1/2 und 3/4.
Beachten Sie, das tiefe Minimum in der Übertragungsfunktion bei 1250 Hz gibt, wo der Peak im zweiten Signal vollständig verschwunden ist.
Es gibt auch ein tiefes Minimum in der Übertragungsfunktion bei 1750 Hz, wo es wiederum kein Peak im Ausgangssignal gibt, und einen scharfen Peak in der Übertragungsfunktion bei 1775 Hz, wo es einen scharfen Peak im Ausgangssignal gibt, aber keinen im Eingangssignal.
Eine Übertragungsfunktion auf Eingangsdaten anwenden
Beachten Sie, dass es für reale Anwendungen nicht viel Sinn macht, eine Übertragungsfunktion anhand von Signalen zu berechnen, wie sie in den vorherigen Abschnitten verwendet wurden. Es ist erkennbar, dass Signal B keine Antwort eines LTI-Systems (Linear Time-Invariant System) sein kann, da eine Frequenzverschiebung auftrat während LTI-Systeme nur die Phasen und Amplituden vorhandener Spektralkomponenten variieren. Des Weiteren sollte das Eingangssignal alle "Frequenzen im" LTI-System anregen, um ein vollständiges Bild des LTI-Systems und damit eine wohl definierte Übertragungsfunktion zu erhalten. Ein solches Eingangssignal wäre z. B. weißes Rauschen.
Um dies zu demonstrieren, enthält die Beispieldatenbank einen weiteren Datensatz Input Noise und ein Objekt mit dem Namen Output Noise, welche eine Tiefpass-gefilterte Version des Eingangsrauschens ist. Das Objekt Transferfunction wurde bereits angelegt, um die Übertragungsfunktion des Tiefpasses anhand dieser Signale zu berechnen. Ein Diagramm mit gleichem Namen visualisiert diese. Der Tiefpass ist ein Butterworth-Filter der Ordnung 4 mit einer Grenzfrequenz von 100Hz.
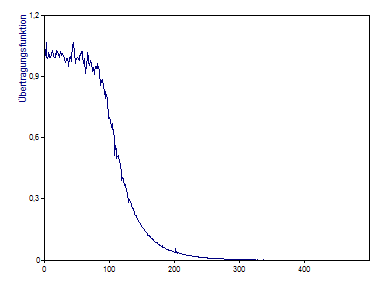
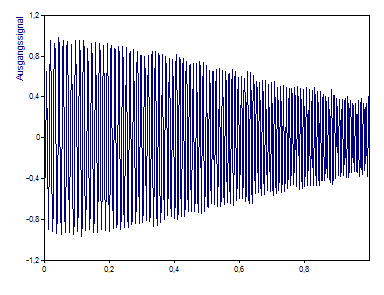
Als letzte Übung soll die Übertragungsfunktion auf ein Eingangssignal angewendet werden, um das Ausgangssignal abzuschätzen. Markieren Sie das Objekt Input Signal, welches einen Wobbelsinus darstellt, dessen Frequenz von 75Hz auf 125Hz linear ansteigt. Klicken Sie mit der rechten Maustaste, zeigen Sie auf Objekt einfügen und klicken Sie dann auf Formel. Geben Sie die folgende Formel ein: IRFFTn(FFTn(Eingangssignal) * Übertragungsfunktion). Klicken Sie nun auf Ausführen, um die Formel zu testen. Sie sollten ein Signal mit 1000 Punkten erhalten. Klicken Sie auf OK und schließen Sie das Formel-Fenster. Markieren Sie den Namen der Formel nochmals und Klicken Sie auf die F2-Taste. Geben Sie nun den neuen Namen Ausgangssignal ein. Die Formel berechnet das Spektrum des Eingangssignals und multipliziert dies mit der Übertragungsfunktion. Diese einfache Berechnung ist möglich, da eine Faltung im Zeitbereich einer einfachen Multiplikation im Frequenzbereich entspricht. Wenn Sie die Spektren multiplizieren, dann müssen Sie darauf achten, dass die Anzahl der Frequenzen und die Frequenzschrittweiten beider Spektren identisch sind. Um dieses Tutorial so einfach wie möglich zu halten, wurde die Übertragungsfunktion aus einem einzigen Segment berechnet, dessen Länge dem Eingangsrauschen und auch dem Wobbelsinus-Signal entspricht. Wenn wir überlappende Segmente gemittelt hätten, wäre die Übertragungsfunktion sowohl glatter als auch kürzer geworden.
Wir haben einen Datensatz mit 1000 reellen Werten berechnet, dessen Amplitude mit steigender Frequenz abfällt. Die Grenzfrequenz von 100Hz wird genau in der Mitte des Wobbelsinus-Signals erreicht. Dort ist die Amplitude des Ausgangssignals wie erwartet um -3dB gedämpft.
Literatur
•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.
Siehe auch
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen