Tutorial Zeit-Frequenz-Spektralanalyse
Dieses Tutorial behandelt Fourier-Spektralanalyse in FlexPro für nichtstationäre Daten. Dies umfasst sowohl die Kurzzeit-Fourier-Transformation (STFT) also auch die Kontinuierliche Wavelet Transformation (CWT). Diese Prozeduren sind für die Untersuchungen sich verändernder Eigenschaften innerhalb eines Datensatzes nützlich. Es lassen sich ebenfalls stationäre Gebiete für die konventionelle Fourier-Analyse und die parametrische Spektralanalyse ausfindig machen.
Ein Testsignal mit vier sequentiellen Sinuskurven
Für dieses Tutorial wird ein nichtstationärer Datensatz mit vier Bereichen verwendet, die jeweils eine Sinuskurve unterschiedlicher Frequenz enthalten.
Wählen Sie Datei > Projektdatenbank öffnen und öffnen Sie die Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Tutorials\Spectral Analysis.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021>Examples>Tutorials>Spectral Analysis.fpd. Öffnen Sie den Ordner Tutorials und darin den Unterordner Time-Frequency Analysis und öffnen Sie das 2D-Diagramm Data per Doppelklick.
Dies ist die Abbildung des Signals, das 1024 Fließkomma-Werte enthält.
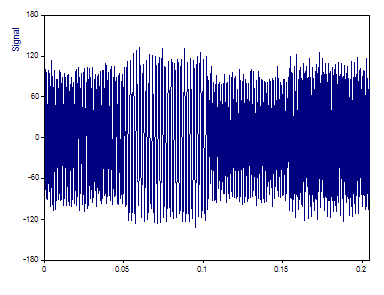
Die x-Werte (Zeit) variieren von 0 bis 0,2047 bei einem Abtastintervall von 0,0002. Die Nyquist-Frequenz ist daher 2500 Hz (Hälfte der Abtastfrequenz von 5000 Hz). Die vier Sinuskurven wurden mit folgenden Amplituden, Frequenzen und Phasen erzeugt:
100.0*sin(2π*x*1000)+
120.0*sin(2π*x*500+p/2)+
90.0*sin(2π*x*2000+p)+
110.0*sin(2π*x*1500+3p/2)
10% zufälliges weißes Rauschen wurde hinzugefügt, d. h. der Pegel des Hintergrundrauschens liegt bei -20 dB.
Der Verlust der Zeitinformation bei der Fourier-Transformation
Beginnen Sie damit, sich das einfache Fourier-Spektrum dieses Datensatzes anzusehen.
Schließen Sie das Diagramm und markieren Sie den Datensatz Signal.
Klicken Sie auf Einfügen[Analysen] > Analyse-Assistent.
Wählen Sie die Kategorie Fourier-Analyse unter Spektralanalyse aus. Dort wählen Sie Fourier-Spektrum aus. Klicken Sie auf die Weiter-Schaltfläche.
Als Spektrumtyp wählen Sie Amplitude. Als Fenstertyp wählen Sie Rechteck -13dB W=1. Stellen Sie sicher, dass die FFT-Länge auf die Datensatzlänge oder 1024 gesetzt wird. Wählen Sie die Maximale Peak-Anzahl Option und geben Sie dort den Wert 4 ein. Setzen Sie anschließend Kritische Grenze Weißes Rauschen % auf Keine. Falls über den Peaks keine Beschriftungen sichtbar sind, klicken Sie auf Beschriftungen, bis die Amplituden-Beschriftungen erscheinen.
Die Darstellung des Fourier-Spektrums im Analyseassistenten sollte folgendermaßen aussehen:
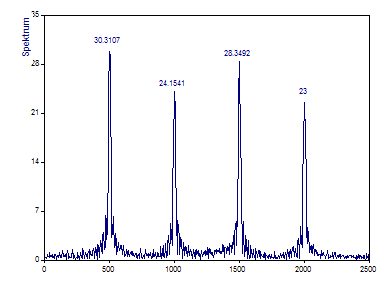
Während das Fourier-Spektrum die Frequenzen der vier sequentiellen Komponenten richtig identifiziert, gibt es keinen Hinweis darüber, wo diese Harmonischen im Zeitbereich beginnen oder enden. Alle Informationen über den Zeitbereich sind verloren gegangen, da jede Komponente eine unendliche Zeitdauer annimmt.
Da jede der Komponenten nur für ungefähr ein Viertel der gesamten Datensatzlänge sichtbar ist, hat jede Amplitude näherungsweise nur ein Viertel des eigentlichen Wertes der transienten Harmonischen.
Ein Signal sollte im weiteren Sinne stationär sein, um für ein Fourier-Spektrum geeignet zu sein. Das bedeutet, dass die Spektren sowohl in der Frequenz als auch in der Leistung über die Abtastzeitdauer konstant sein sollten. Sowohl die CWT als auch die STFT ist zur Analyse nichtstationärer Signale besser geeignet, da sie ein Zeit-Frequenz-Spektrum der Daten liefern.
Kurzzeit-Fourier-Transformation Spektrum
Die Kurzzeit-Fourier-Transformation (STFT) ähnelt dem Periodogramm bzw. der überlappend-segmentierten FFT, außer dass jedem Segment der zentrale Zeitwert zugeordnet, der seiner zeitlichen Position in der Datenreihe entspricht. Solange die Amplitude oder Leistung nicht direkt aus den Peaks ermittelt werden muss, wird normalerweise ein Bewertungsfenster benutzt, um die best mögliche Zeitlokalisierung zu erreichen.
Zeit-Frequenz-Spektren sind an sich unscharf. Je besser die Auflösung der Zeit ist, desto schlechter wird die der Frequenz und umgekehrt. Die STFT ist der beste Weg, ein Gefühl für diesen Effekt zu erlangen.
Klicken Sie auf die Zurück-Schaltfläche, um zu Schritt 1 des Analyseassistenten zu gelangen. Wählen Sie die Kategorie Zeit-Frequenz-Analysen und dort STFT. Klicken Sie auf Weiter, um zu Schritt 2 zu gelangen. Die Kurzzeit-Fourier-Transformation (STFT)-Prozedur ist schon automatisch ausgewählt.
Als Spektrumtyp wählen Sie dB, normiert. Setzen Sie Fenstertyp auf Cos2 Hanning -31dB W=2. Die Standardwerte werden als Ausgangspunkt gewählt. Stellen Sie sicher, dass FFT-Länge auf Segmentlänge gesetzt wird, die Segmentlänge den Wert 256 hat, was einem Viertel der Datenlänge entspricht. Die Überlappung % setzen Sie auf 50.
Um die Zeit der x-Achse zuzuordnen, wie es bei Zeit-Frequenz-Spektren oft gemacht wird, wählen Sie Frequenz ist Z aus. Setzen Sie Maximaler dB-Bereich auf 20 und lassen Sie Maximale Anzahl STFT Frequenzwerte auf unbeschränkt stehen.
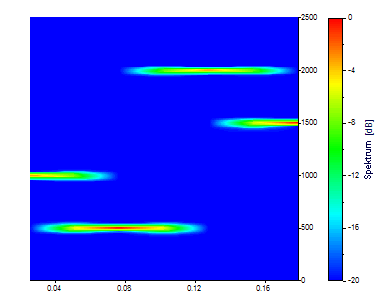
Diese Einstellungen produzieren sieben Zeit-Schnappschüsse, jedes mit der Länge 0,05 Sekunden. Es gibt 129 Frequenzen. Während bei den Frequenzen 500, 1000, 1500 und 2000 die Komponenten stark definiert sind, ist dies aufgrund der sequentiellen Eigenschaft der Harmonischen nicht der Fall für die Zeitachse. Da die Zeit, die einem Schnappschuss zugeordnet wird, außerdem die Zeit der Segmentmitte ist, gibt es an beiden Enden des Zeitintervalls einen ausgedehnten Bereich, für den keine Spektralinformation vorliegt.
Eine einfache Möglichkeit, die Anzahl der Zeitpunkte zu vergrößern, ist den Wert Überlappung % zu vergrößern.
Ändern Sie Überlappung % auf 90.
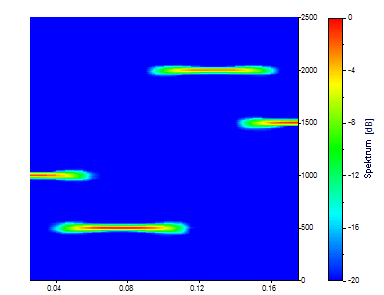
Jetzt gibt es 31 unterschiedliche Zeit-Schnappschüsse, die dieses Spektrum bilden. Es sind die gleichen 129 Frequenzen vorhanden. Während die Zeitauflösung eine bescheidene Verbesserung erfährt, ist jeder Schnappschuss immer noch ein Durchschnitt über ein Viertel der Daten. Um die Zeitauflösung zu verbessern, muss die Segmentlänge verkleinert werden.
Um die Segmentlänge zu halbieren, geben Sie den Wert 128 ein. Behalten Sie Überlappung % auf dem Wert 90 bei.
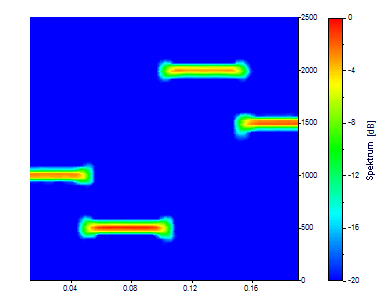
Es gibt jetzt 75 Zeitsegmente, jedes erstreckt sich über einem Achtel der Daten. Es gibt 65 Frequenzen. Der Kompromiss zwischen Zeit und Frequenz sollte jetzt ersichtlich werden. Es gibt jetzt eine höhere Präzision im Zeitbereich, aber die Frequenzauflösung hat sich deutlich verschlechtert.
Ändern Sie Segmentlänge auf 64.Behalten Sie Überlappung % auf dem Wert 90 bei.
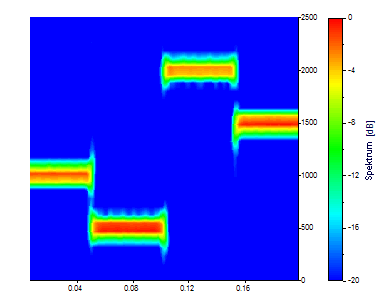
Es gibt jetzt 161 Zeitsegmente, jedes erstreckt sich über ein Sechszehntel der Daten. Es gibt 33 Frequenzen. Die Schärfe bei der Zeit hat sich weiterhin verbessert, die Frequenzauflösung wurde wesentlich unschärfer. Gehen Sie noch einen Schritt weiter, indem Sie Segmentlänge auf 32 ändern. Behalten Sie Überlappung % auf dem Wert 90 bei.
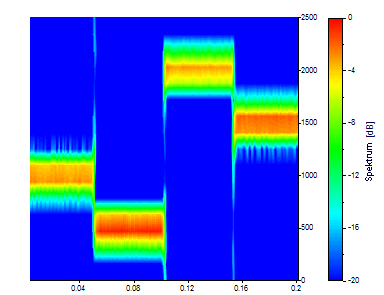
Es gibt jetzt 331 Zeitwerte, aber nur noch 17 Frequenzen. Die Zeit-Schnappschüsse repräsentieren jeweils ein Zweiunddreißigstel der Daten. Daher ist die Zeitabgrenzung ziemlich scharf. Dagegen stoßen die Peaks im Frequenzbereich schon fast aneinander.
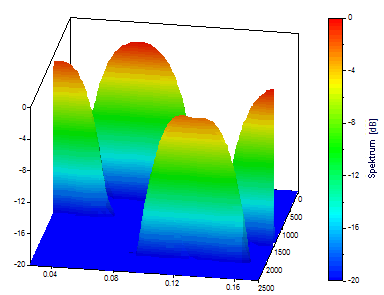
Die Visualisierung wird bei einer 3D-Oberflächendarstellung ersichtlicher.
Klicken Sie auf Standardansicht. Um die Ansicht zu verbessern, ändern Sie FFT-Länge auf 128.

Dies zeigt den Kompromiss zwischen Zeit und Frequenz sehr schön. Kehren Sie nun zu den ursprünglichen Einstellungen, die die Frequenz bevorzugen, zurück.
Setzen Sie Segmentlänge auf 256, die FFT-Länge auf Segmentlänge und Überlappung % auf 90.
Diese Darstellung gibt den Zeit-Frequenz-Kompromiss bei einer guten Frequenzauflösung und einer deutlichen Zeitunschärfe wieder.
Die Optimierung der STFT-Parameter kann eine Herausforderung sein. Die STFT ist eine Analyse mit fester Auflösung. Die STFT erfordert zwar eine vorsichtige Feineinstellung der Parameter, andererseits kann ein STFT-Spektrum verwendet werden, um die Amplituden und Leistungen direkt als Höhen der Peaks abzulesen. Verwenden Sie entweder ein Bewertungsfenster und stellen Sie die Normierung auf Amplitude oder verwenden Sie ein Rechteckfenster in Verbindung mit sehr hoher Überlappung.
Die folgende Grafik erhalten Sie, wenn Sie den Spektrumtyp auf Amplitude, den Fenstertyp auf Rechteck -13dB W=1 (keine Fensterung), Segmentlänge auf 64, FFT-Länge auf 256 und Überlappung % auf 90 stellen.
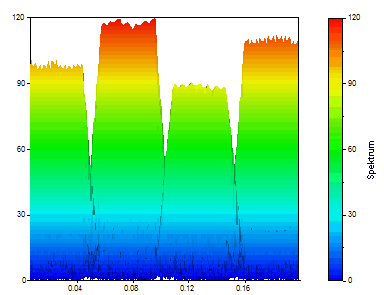
Kontinuierliche Wavelet-Transformation
Die STFT verwendet phasenverschobene Sinusfunktionen. Die zeitliche Unbeschränktheit der Sinus-Funktionen erfordert die Transformation fensterbewerteter Segmente des Datensatzes. Wenn die Elementarfunktionen selbst von endlicher Dauer wären, könnte ein Spektrum aus der Korrelation zwischen verschobenen und gedehnten/gestauchten Versionen dieser Mutter-Wavelets endlicher Dauer und dem Datensatz ermittelt werden.
Dies ist das Prinzip der Kontinuierlichen Wavelet Transformation (CWT).
Trotz der großen Anzahl an Wavelet-Formen ist die Verwendung von Wavelets für die Zeit-Frequenz-Spektralanalyse im Allgemeinen einfacher als die Optimierung der STFT. In den meisten Fällen wirken sich die verschiedenen Mutter-Wavelets und Einstellungen nicht erheblich auf das Ergebnis des Zeit-Frequenz-Spektrums aus. Die Auswahl des Mutter-Wavelets und der Parameter ist mit dem Kompromiss zwischen Zeit- und Frequenzauflösung verknüpft.
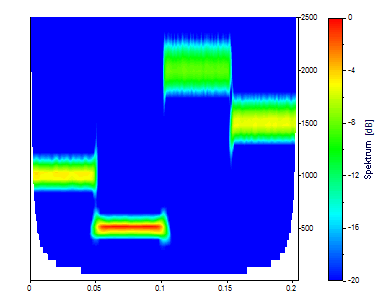
Wählen Sie Kontinuierliche Wavelet Transformation (CWT) und dB, normiert als Spektrumtyp. Setzen Sie Wavelet-Typ auf Morlet und Anpassung (Wellenzahl) auf 8. Setzen Sie Nullen anhängen auf 1024 (füllt den Datensatz mit 1024 Werten auf 2048 Werte auf), die Frequenzanzahl auf 40 und lassen Sie Anfangsfrequenz auf 0 und Endfrequenz auf 2500 (der volle Nyquist-Bereich). Stellen Sie sicher, dass Frequenz ist Z aktiviert ist, der Maximaler dB-Bereich auf 20 gesetzt ist und, dass Maximale Anzahl CWT Zeitwerte den Wert 1024 hat (um die gesamte Datensatzlänge aufzunehmen).

Dies ist ein gutes CWT Zeit-Frequenz-Spektrum. Tatsächlich wurden respektable Ergebnisse erreicht, ohne dass Mutter-Wavelet oder den Wert seines verstellbaren Parameters zu ändern. Sie könnten das Morlet-Wavelet immer mit einer Wellenzahl von 8 verwenden und würden nie die Optimierungen vermissen, die sich durch die optimale Wahl des Wavelets und die Einstellung dessen Anpassungswertes für eine optimale Zeit-Frequenzauflösung ergeben würden.
Um das zu sehen, werden Sie jetzt die Extrema, die in FlexPro angeboten werden, betrachten.
Um den Zeit-Frequenz-Kompromiss in der Wavelet-Analyse aufzudecken, wird wieder ein Konturdiagramm dargestellt. Klicken Sie auf Draufsicht.

Ändern Sie Anpassung auf die Wellenzahl 20.
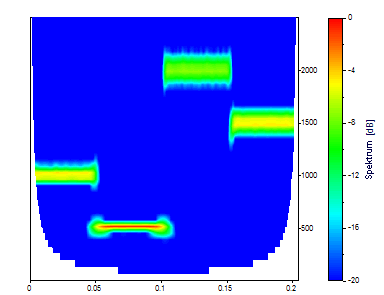
Das Morlet mit einem verstellbaren Parameter (Wellenzahl) von 20 erzeugt eine schärfere Frequenzauflösung, aber eine schlechtere Zeitlokalisierung.
Ändern Sie Anpassung auf 50.
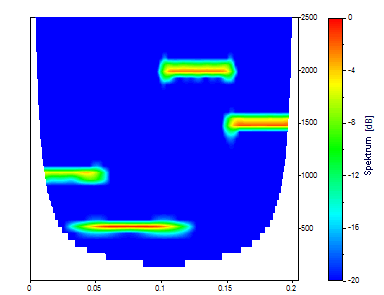
Das Morlet mit einer Wellenzahl von 50 erzeugt eine sehr hohe Frequenzauflösung, aber eine schlechte Zeitlokalisierung.
Setzen Sie den Wavelet-Typ auf Gaussian Derivative und den Wert Anpassung auf 2.

Das Gaussian Derivative-Wavelet mit dem verstellbaren Parameter 2 erzeugt die schärfste Zeitlokalisierung, aber eine sehr verschwommene Frequenzdarstellung.
"Multiresolution"-Analyse
Die CWT ist eine "Multiresolution" Zeit-Frequenz-Methode. Wenn Sie sich die vorherigen Abbildungen anschauen, werden Sie feststellen, dass der Peak mit der niedrigsten Frequenz den größten CWT-Spektralbetrag hat und in der Frequenz von allen vier Signalkomponenten am wenigsten "verschmiert".
Diese Eigenschaft ist eher ein Nebenprodukt des CWT-Algorithmus als ein Ziel bei der Entwicklung des Algorithmus. Die "Multiresolution" Analyse hat Vor- und Nachteile. Falls hohe Frequenzkomponenten für eine kurze Zeitdauer auftreten, ist die beste Wahl, Frequenzauflösung zu opfern, um das Eintreten und Verschwinden der Komponente exakt aufzulösen. Falls niedrige Frequenzkomponenten langlebig sind, ist es am besten, Zeitauflösung gegen eine bessere Frequenzschätzung einzutauschen. Falls diese Aussagen zutreffen, ist die "Multiresolution" Analyse der CWT ein Gewinn.
Falls die Persistenz unabhängig von der Frequenz ist, oder das primäre Ziel darin besteht, die Amplituden und Leistungen direkt aus den Beträgen des Spektrums zu ermitteln, ist die "Multiresolution"-Methode von Nachteil.
Frequenz-Redundanz der CWT
Im Gegensatz zur Diskreten Wavelet-Transformation (DWT), die gewöhnlich für die Wavelet-Analyse benutzt wird, kann die CWT bei beliebigen Frequenzen ausgewertet werden. Diese Frequenzen können durch Überlappung zu einem beliebigen Maß an Redundanz führen und linear, logarithmisch oder in irgendeiner anderen Form angeordnet sein. Weil für jede zu schätzende Frequenz eine getrennte FFT gespeichert werden muss, begrenzt FlexPro die gesamte Frequenzanzahl auf 500. Durch diese Frequenzredundanz bietet die CWT eine viel höhere Auflösung als die DWT.
Wählen Sie das Morlet-Wavelet mit einer Wellenzahl von 12. Geben Sie 100 als Frequenzzahl, 400 als Startfrequenz und 1200 als Endfrequenz ein.

Die CWT-Spektralanalyse konzentriert sich jetzt vollständig auf das Frequenzband 400 bis 1200.
Nullen anhängen bei der FFT und Randeffekte
Im Gegensatz zur konventionellen Fourier-Analyse, deren Spektrum durch Transformation erzeugt wird, wird die bei der CWT benutzte FFT für die schnelle Faltung skalierter und verschobener Wavelets mit dem Datensatz verwendet. Die Basisfunktionen der CWT sind skalierte und verschobene Wavelets, keine Sinus- und Kosinusfunktionen. Das Anhängen von Nullen hat bei der CWT nur das eine Ziel, Spiegelungseffekte (Aliasing) bei der schnellen Faltung zu vermeiden. Dies wird für alle Frequenzen vollständig vermieden, wenn die FFT-Länge zweimal so groß wie die Datensatzlänge ist. Oft ist es sinnvoll, Nullen bis zur nächsten 2er-Potenz anzuhängen, um die Spiegelungseffekte zu unterdrücken und gleichzeitig eine schnelle Berechnung zu erzielen.
Wenn eine exact-N FFT für die schnelle Faltung benutzt wird, ist der Spiegelungseffekt bei niedrigen Frequenzen deutlich sichtbar. Der Spiegelungseffekt verringert sich mit der Frequenzzunahme. Dies erklärt die Abwesenheit von Spiegelungseffekten bei der höchsten Frequenzkomponente. Wenn der Spektralgehalt bei niedrigen Frequenzen vernachlässigbar ist oder die Daten des betrachteten Ausschnittes periodisch sind, dann macht das Anhängen von Nullen keinen Sinn.
Wenn Anhängen von Nullen benutzt wird, um diesen Effekt zu vermeiden, geht die Leistung, die mit dem Spiegelungseffekt verbunden ist, verloren. Das Ergebnis ist eine verringerte Leistung an den Rändern des Datensatzes. Dieses Gebiet mit verringerter Leistung wird bei der CWT auch als "cone of influence" bezeichnet. Der "cone of influence" ist besonders deutlich, wenn der Frequenzabstand logarithmisch ist.
Setzen Sie die Morlet-Wellenanzahl auf 100, Nullen anhängen auf 0, Frequenzanzahl auf 40, Anfangsfrequenz auf 0 und Endfrequenz auf 2500.

In diesem Fall liefert eine hohe Wellenzahl einen größeren "cone of influence". Die Spektralkomponente mit der niedrigsten Frequenz wird hier an den rechten Rand der Zeitskala gespiegelt. Dies wird in FlexPro nicht angezeigt, da die Informationen in diesem "cone of influence" nicht dargestellt werden.
Setzen Sie die Morlet-Wellenzahl auf 12 und klicken Sie auf Weiter. Aktivieren Sie beide Optionen in Schritt 3 und klicken Sie anschließend auf die Beenden-Schaltfläche.
Es werden vier Objekte in der FlexPro-Projektdatenbank erzeugt.
"Spektrum" ist das Analyseobjekt. Es führt die Spektralanalyse aus und lässt sich durch einen Doppelklick öffnen.
"Spektrum" ist die Darstellung des Zeit-Frequenz-Spektrums, das vom Analyseassistenten erzeugt wurde. Es benutzt das "Spektrum"-Objekt.
"Daten2" ist die Darstellung der ursprünglichen Daten des Zeitbereichs.
"Zeit-Frequenz" ist ein Dokument, das die Darstellung des Spektrums und der Daten enthält.
Literatur
Gute Einführungen in die digitale Signalverarbeitung sind:
•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.
•H.D. Lüke (1985). Signalübertragung. Springer-Verlag Berlin, Heidelberg, New York. ISBN 3-540-15526-0.
Die in FlexPro verwendeten FFT-Algorithmen sind hier beschrieben:
•C. Temperton, "Implementation of a Self-Sorting In-Place Prime Factor FFT Algorithm", Journal of Computational Physics, v. 58, p. 283, 1985
•R. C. Singleton, "An Algorithm for Computing the Mixed Radix Fast Fourier Transform", IEEE Trans. Audio Electroacoust., v. AU-17, p. 93, June 1969
•L. R. Rabiner, R. W. Schafer, C. M. Rader, "The Chirp z-Transform Algorithm and Its Application", BSTJ, 48, p.1249, May-June 1969
Informationen über Bewertungsfenster finden Sie in:
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, Feb. 1981.
Für diejenigen, die die Feinheiten der praxisnahen Wavelet-Analyse verstehen möchten, sei folgendes Dokument empfohlen:
•Christopher Torrence and Gilbert Compo, "A Practical Guide to Wavelet Analysis", Bulletin of the American Meteorological Society, v.79, no.1, p.61-78. January 1998
Diese Arbeit erklärt die CWT im Zusammenhang mit der Analyse der El Niño Zeitwerte. Die Autoren haben außerdem das FORTRAN-Paket (public domain) WAVEPACK für die Wavelet-Analyse veröffentlicht. Sowohl das Dokument als auch der WAVEPACK-Code kann man unter http://paos.colorado.edu/research/wavelets/ finden.
Siehe auch
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen