Kreuzspektrum und Kreuzperiodogramm

Das Kreuzspektrum and das Kreuzperiodogramm messen die gemeinsame spektrale Leistung zweier Signale.

Die Berechnung erfolgt über die elementweise komplexe Multiplikation der ersten Fourier-Reihe mit der konjugiert-komplexen zweiten Fourier-Reihe. Die Normierung basiert auf dem Kehrwert der Datensatzlänge:

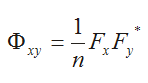
Wenn man die konjugiert-komplexe Multiplikation berechnet, erhält man:

(Re{Fx}, Im{Fx}) * (Im{Fx}, Im{Fy}) = (Re{Fx} * Re{Fy} + Im{Fx} * Im{Fy}, Im{Fx} * Re{Fy} + Re{Fx} * Im{Fy})

Der Realteil des Ergebnisses enthält die gleichphasigen Spektralanteile und der Imaginärteil die orthogonalen Spektralanteile.

Der Realteil kann auch geschrieben werden als:

Re{Fx} * Re{Fy} + Im{Fx} * Im{Fy} = |Fx| * |Fy| * cos(jxy), mit dem Phasenwinkel jxy zwischen Fx und Fy.

Alle reellen Spektralformate verwenden nur den Realteil. Werden diese Spektralformate für zwei identische Datensätze angewendet, dann liefern das Kreuzspektrum und das Kreuzperiodogramm die gleichen Spektren wie das Fourier-Spektrum oder Periodogramm für einen Datensatz.

Die Reihenfolge von x und y beeinflusst lediglich den Imaginärteil des Spektrums. Das Kreuzspektrum von x und y ist gleich dem konjugiert-komplexen Kreuzspektrum von y und x.

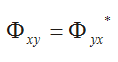
Kohärenz

Wenn zwei Signale aus einer gemeinsamen Quelle stammen, dann liefert die Kohärenz-Analyse ein Maß für die Gleichartigkeit oder für die lineare Abhängigkeit des einen Signals vom anderen. Das am häufigsten verwendete Maß für die Kohärenz ist die Magnitudenquadrat-Kohärenz, "magnitude squared coherence" (MSC):

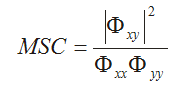
Der Verlauf der Kohärenz variiert im Bereich von 0 bis 1. Eine Kohärenz von 0 für eine gegebene Frequenz zeigt an, dass die Signale bei dieser Frequenz keine Gemeinsamkeit haben. Ein Kohärenz-Wert von 1 für eine gegebene Frequenz bedeutet, dass der spektrale Inhalt beider Signale bei dieser Frequenz identisch ist. Die Kohärenz zwischen den Signalen x und y entspricht der Kohärenz zwischen den Signalen y und x.

Signal-Rausch-Verhältnis Spektren

Wenn das mit zwei von einer gemeinsamen Quelle stammenden Signalen verbundene Rauschen unkorreliert ist, was im Allgemeinen für weißes Hintergrundrauschen zutrifft, dann kann das Signal-Rausch-Verhältnis (Signal-to-Noise-Ratio - SNR) wie folgt berechnet werden:

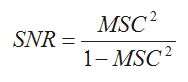
Das Signal-Rausch-Verhältnis ist, wie die Kohärenz, von der Reihenfolge von X und Y unabhängig.

Übertragungsfunktion

Das Ausgangssignal eines linearen Systems ist mit dessen Eingangssignal über die Übertragungsfunktion verknüpft, welche aus dem Leistungsdichtespektrum des Eingangssignals und dem Kreuzspektrum zwischen Eingangs- und Ausgangssignal berechnet werden kann:

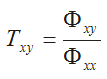
Literatur

•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.