Tutoriel Estimation harmoniques
Ce tutoriel couvre les capacités d'analyse spectrale de FlexPro relatives à la modélisation harmonique et aux mesures de distorsion harmonique.
Analyse de Fourier
Si vous ne l'avez pas encore fait, il est recommandé de passer par les tutoriels sur l'Analyse de Fourier et l'Estimateur spectral avant de commencer celui-ci. La première étape de l'estimation des harmoniques de FlexPro est une estimation entièrement automatique de la fréquence, généralement réalisée via une analyse de Fourier, une analyse spectrale AR, ou une analyse propre.
Un signal d'essai harmonique avec distorsion et bruit
Pour ce tutoriel, nous utiliserons un signal de longueur 1024. Il y aura une harmonique primaire, et un certain nombre d'harmoniques secondaires à des multiples de la fréquence de la primaire :
100.0*sin(2π*x*250+p/4)
10.0*sin(2π*x*500+p/2)
1.0*sin(2π*x*750+p)
0.1*sin(2π*x*1000+3p/2)
0.01*sin(2π*x*1250+7p/4)
La fréquence d'échantillonnage est de 5000 Hz, et par conséquent la fréquence de Nyquist est de 2500 KHz, la fréquence maximale pouvant être détectée. Les valeurs de temps varient de 0 à 0,2046 à un incrément de 0,0002 échantillon. 0.01% de bruit gaussien aléatoire a été ajouté. Cela produit un plancher de bruit à environ -100 dB par rapport à la plus grande crête.
Sélectionnez la commande Fichier > Ouvrir Base de données projet et ouvrez la base de données projet C:\Users\Public\Documents\Weisang\FlexPro\2021\Exemples\Tutoriels\Analyse spectrale.fpd ou C:>Utilisateurs>Public>Documents Public>Weisang>FlexPro>2021>Exemples>Tutoriels>Analyse spectrale.fpd. Ouvrez le dossier Tutoriels et son sous-dossier Estimation harmonique, puis double-cliquez pour ouvrir le graphique 2D appelé Données.
C'est un graphique du signal. Il y a 1024 valeurs à virgule flottante.
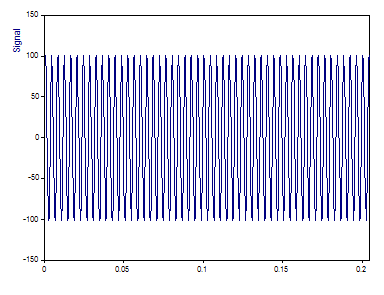
Seule l'harmonique principale est apparente dans le domaine temporel. Les harmoniques secondaires représentent une distorsion harmonique très importante.
Bien qu'il soit possible de déterminer le nombre de composantes harmoniques sans le faire, nous allons d'abord explorer le Spectre de Fourier de ce signal.
Spectres de Fourier
Fermez la fenêtre du graphique et mettez en évidence l'ensemble de données Signal.
Cliquez sur Insérer[Analyses] > Assistant d'analyse.
Sélectionnez la catégorie Analyse de Fourier sous Analyses spectrales. Ensuite, sélectionnez Spectre de Fourier. Cliquez sur Suivant.
Pour le Type de spectre, sélectionnez dB normalisé. Pour le type de fenêtre, sélectionnez Tchebyshev et entrez 4 pour le paramètre ajustable de la fenêtre. Assurez-vous que la longueur de la FFT est fixée à 16384. Sélectionnez l'option Nombre maximal de pics et entrez la valeur 5. Ensuite, définissez la limite critique du bruit blanc % sur Aucun. Si aucune étiquette n'est visible au-dessus des pics, cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes dB s'affichent.
Le tracé de Fourier dans l'assistant d'analyse devrait être le suivant :
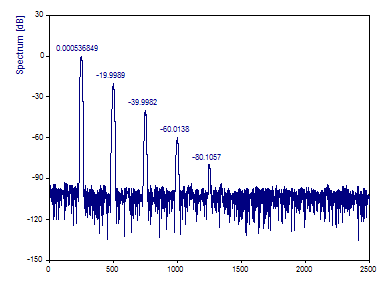
Il est clair que les harmoniques secondaires sont caractérisées avec précision par le spectre de Fourier.
Cliquez sur Basculer les étiquettes jusqu'à ce que les fréquences soient affichées.
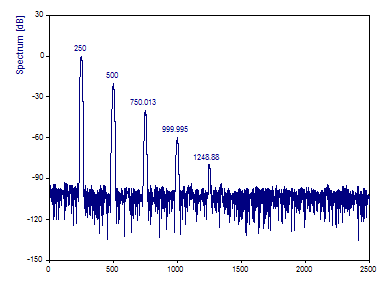
Les fréquences de l'harmonique principale ainsi que des secondaires sont également estimées avec précision à partir de ce spectre de Fourier optimisé.
Méthodes de Fourier pour l'identification des fréquences
Les conditions que nous avons utilisées pour le spectre de Fourier représentent celles qui sont mises en œuvre automatiquement dans la procédure d'estimation des harmoniques qui utilise l'analyse de Fourier pour l'identification des fréquences. Dans tous les cas, la fenêtre d'observation de données de Tchebyshev est utilisé et sa largeur unilatérale dans le domaine fréquentiel est réglée automatiquement. Pour les longueurs de données de 256 et moins, cette largeur est fixée à 2. Pour les longueurs de données supérieures à 1024, la largeur de la fenêtre est fixée à 4. Entre ces valeurs, cet ajustement de la fenêtre varie logarithmiquement de -6+1.4427ln(n). Cela produit une largeur de domaine de fréquence de 3 pour une longueur de données de 512. Le rajout de zéro (zero padding) est effectué pour créer une FFT de longueur 16384 si la longueur des données est inférieure à 16384.
L'utilisation de l'analyse de Fourier pour l'identification des fréquences présente deux inconvénients. La première est que, même avec la fenêtre d'observation des données, le rajout de zéro (zero padding) et l'interpolation bin, la précision de l'estimation de la fréquence peut être inférieure à celle des procédures AR ou Eigenanalysis. Cela est particulièrement vrai si la longueur des données est de l'ordre de mille points ou moins. L'analyse de Fourier pour l'identification des fréquences n'est pas recommandée si la longueur des données est nettement inférieure, par exemple quelques centaines de points.
Un autre problème tout aussi important est que l'analyse de Fourier produit parfois une caractéristique spectrale nette sur la montée et la descente d'un grand pic spectral. La fenêtre de Tchebyshev a été sélectionnée pour minimiser cet effet, mais il peut encore se produire, en particulier avec le rajout de zéro (zero padding) mis en œuvre pour améliorer les estimations de fréquence. Étant donné que l'analyse harmonique peut inclure quelques harmoniques pour modéliser les tendances dans le bruit, et ainsi améliorer encore la précision du signal de modélisation des composantes, il est important que les pics sur les épaules de l'harmonique principale ne soient pas enregistrés de manière significative dans le modèle harmonique.
Il s'agit du spectre de Fourier, exactement comme ci-dessus, sauf que la fenêtre de Blackman-Harris de -92 dB est utilisée et que 10 pics sont détectés.
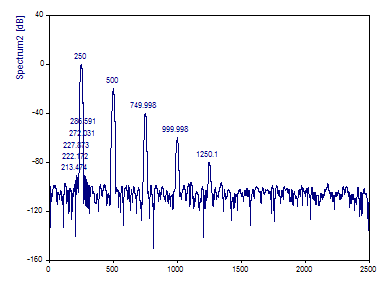
Notez que les cinq pics supplémentaires se produisent tous sur les épaules du pic de l'harmonique principale. Dans ce cas, il ne sera pas possible d'inclure des harmoniques supplémentaires pour modéliser le bruit. Au contraire, il est essentiel que seules cinq harmoniques soient incluses dans le modèle.
Estimation harmonique
L'objectif de l'estimation des harmoniques est de modéliser un signal avec des sinusoïdes à bande étroite ou des sinusoïdes amorties. Le produit de l'analyse est un ensemble d'harmoniques définis par l'amplitude, la fréquence et la phase, ainsi que par des facteurs d'amortissement dans le cas de sinusoïdes amorties.
Cliquez sur Précédent. Sélectionnez la catégorie Analyses harmoniques sous Analyse spectrale. Ensuite, sélectionnez Estimation harmonique. Cliquez sur Suivant. Sélectionnez pour l'Algorithme Fourier et pour le Modèle Sinusoïde. Définissez le nombre de composants Par compte maximum et entrez 10. Le type de résultat est Composantes harmoniques. Cliquez sur Basculer les étiquettes jusqu'à ce que les amplitudes soient affichées.
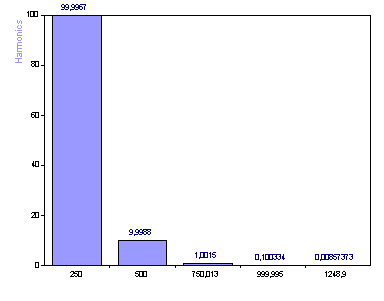
Bien qu'il soit possible de lire les amplitudes à partir des étiquettes, ce n'est pas une bonne visualisation. Une échelle logarithmique est nécessaire pour afficher correctement la large gamme dynamique des amplitudes.
Cliquez sur Suivant pour passer à l'étape 3 de l'assistant. Cochez la case la plus haute et sélectionnez ensuite le graphique 2D portant le nom Harmoniques. Vérifiez l'axe Y logarithmique. Cliquez sur Retour pour revenir à l'étape 2 de l'assistant.
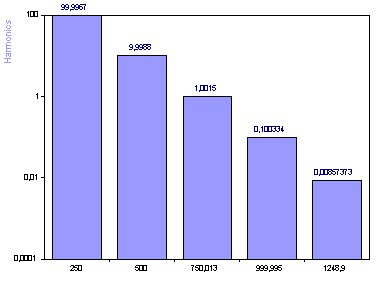
L'algorithme de modélisation harmonique est une procédure en deux étapes. Le pas de Fourier est utilisé uniquement pour estimer les fréquences où le contenu spectral est présent. Les informations d'amplitude ou de puissance du spectre de Fourier ne sont pas utilisées pour l'estimation des harmoniques. Dans ce cas, la méthode de Fourier a été utilisée pour déterminer les 10 fréquences ayant le contenu spectral le plus significatif dans le domaine des fréquences. Le Spectre harmonique illustré ici est créé par un ajustement sinusoïdal linéaire des moindres carrés dans le domaine temporel. Les quatre premières amplitudes sont déterminées avec une grande précision. La cinquième harmonique a une erreur supérieure à 10%. Les harmoniques restantes étaient destinées à modéliser le bruit présent. Comme le bruit blanc est uniformément distribué sur toutes les fréquences, et que ce n'est pas le cas ici, le nombre d'harmoniques doit être fixé au nombre réel d'harmoniques du signal.
Bien que nous ayons une bonne confirmation des cinq pics du signal par une inspection visuelle du spectre de Fourier, ce n'est pas aussi clair dans l'ajustement harmonique basé sur les fréquences de Fourier. Il n'y a pas de démarcation claire entre le signal et le bruit.
Sélectionnez l'algorithme AR Data Matrix FB SVD. Définissez l'ordre du modèle à 40.
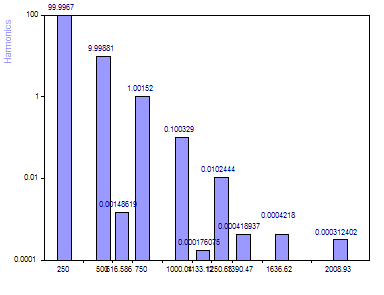
Lorsque l'algorithme AR SVD est utilisé pour l'identification des fréquences, il y a clairement cinq composantes au-dessus du plancher de bruit. De plus, comme les fréquences ont été estimées avec plus de précision, les amplitudes de l'ajustement linéaire sinusoïdal sont également plus précises. En outre, les harmoniques supplémentaires sont réparties beaucoup plus uniformément sur les fréquences, comme on pourrait s'y attendre en capturant une partie de la tendance du bruit aléatoire.
Sélectionnez l'algorithme EigenAnalysis Root MUSIC.
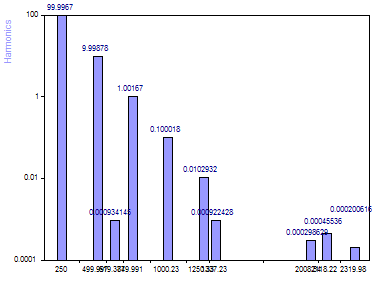
Lorsque l'algorithme MUSIC d'analyse propre est utilisé pour l'identification des fréquences, il y a aussi clairement cinq composantes au-dessus du plancher de bruit. La précision des amplitudes provenant de l'ajustement linéaire sinusoïdal est très proche de celle de la méthode AR.
La méthode AR SVD utilise strictement les modes propres du signal pour estimer les fréquences. L'analyse propre utilise strictement les modes propres du bruit pour estimer les fréquences. L'un ou l'autre peut être plus précis dans une modélisation donnée. Il est souvent judicieux de vérifier les deux. Notez que les cinq fréquences du signal correspondent presque exactement pour les deux procédures. Les cinq harmoniques ajoutées pour modéliser le bruit se chevauchent beaucoup moins.
Paramètres des Composantes Harmoniques
Le bruit blanc doit être non corrélé. Cela signifie qu'il ne doit pas y avoir de tendance ou de persistance. L'amplitude du bruit à une fréquence discrète donnée ne doit pas avoir d'incidence sur son amplitude à la fréquence suivante. Si le bruit est parfaitement non corrélé, nous ne verrons aucun avantage des harmoniques supplémentaires utilisées pour ajuster les tendances dans le bruit.
Pour modéliser uniquement les cinq composantes du signal, réglez le nombre maximum sur 5.
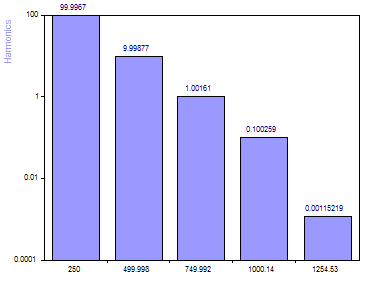
Notez que l'harmonique secondaire de plus faible puissance (amplitude 0,01) n'est plus estimée avec précision. En fait, son amplitude estimée a chuté à près d'un dixième de sa valeur réelle. Alors que nous disposions de cinq harmoniques pour modéliser les oscillations aléatoires du bruit lorsque nous avons spécifié 10 harmoniques dans l'ajustement, nous n'avons maintenant que les cinq composantes réelles du signal à ajuster. Le bruit a un impact négatif sur l'ajustement de cette harmonique secondaire de moindre puissance.
Définissez le Nombre maximal à 10. Cliquez sur Suivant. À l'étape 3, sélectionnez les deux premières options de résultat et cliquez sur Terminer. Double-cliquez sur HarmonicAnalysis.
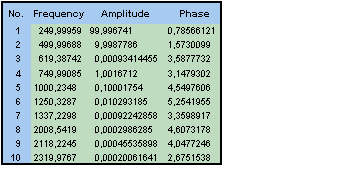
Les fréquences, les amplitudes et les phases des cinq composantes du signal sont estimées avec une grande précision. Comme c'est le cas dans la modélisation harmonique, les fréquences auront l'erreur fractionnelle la plus faible, les amplitudes seront les suivantes et les phases présenteront l'erreur fractionnelle la plus élevée. Les erreurs d'amplitude se situent entre les deux. Plus la puissance d'un composant donné est élevée, plus la précision aura tendance à être grande pour les paramètres définissant cette harmonique.
Distorsion harmonique
La DHT, ou distorsion harmonique totale, est le rapport entre la racine carrée de la somme des puissances ou des amplitudes au carré de toutes les fréquences harmoniques supérieures à la fréquence fondamentale et l'amplitude de la fréquence fondamentale.
Traditionnellement, les FFT étaient utilisées pour mesurer le THD. En raison du contenu spectral qui déborde sur les cases adjacentes avec le fenêtrage, ou de la fuite spectrale qui se produit lorsqu'on utilise un spectre de Fourier non fenêtré, il est très difficile de calculer un THD précis à l'aide d'une FFT. Ceci est particulièrement vrai si le bruit doit être omis et que seules les harmoniques secondaires doivent être incluses.
La modélisation harmonique de FlexPro permet d'obtenir une estimation précise du THD réel. Nous savons que le THD correct pour ce signal de test est sqrt(10²+1²+0.1²+0.01²) / 100. Cela représente 10,05 %.
Les paramètres que nous avons utilisés pour la modélisation harmonique sont également appropriés pour un spectre de distorsion harmonique.
Mettez en surbrillance l'ensemble de données Signal.
Cliquez sur Insérer[Analyses] > Assistant d'analyse.
Sélectionnez la catégorie Analyses harmoniques sous Analyse spectrale. Ensuite, sélectionnez Estimation harmonique. Cliquez sur Suivant.
Sélectionnez l'Algorithme EigenAnalysis Root MUSIC et le Modèle Sinusoïde. Définissez le nombre de composants Par compte maximum à 5. Pour le type de spectre, sélectionnez Spectre de distorsion harmonique %. Cliquez sur Basculer les étiquettes jusqu'à ce que les % de distorsions soient affichés.
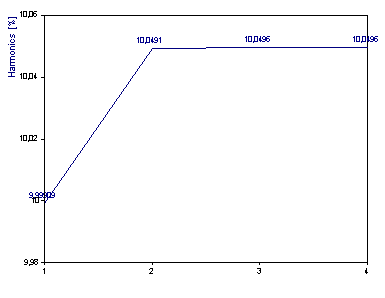
Le nombre de composants est indiqué sur l'axe des abscisses. Au niveau de la composante 2, la distorsion harmonique entre la première harmonique secondaire et la composante principale est tracée. Dans le composant 3, la distorsion harmonique associée aux première et deuxième harmoniques secondaires est tracée. Ainsi le THD (bruit absent) est la valeur au composant quatre. La valeur de 10,0497 est très proche de la valeur 10,0504 que nous savons être correcte. Si vous réglez à nouveau le nombre de composantes à 10, vous constaterez que les composantes de bruit supplémentaires ne contribuent pas de manière substantielle au THD.
Cliquez sur Terminer pour fermer l'assistant d'analyse.
Voir aussi
Vous serez probablement intéressé par les articles suivants :
Vous êtes actuellement en train de consulter le contenu d'un espace réservé de Facebook. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous devez charger le contenu de reCAPTCHA pour soumettre le formulaire. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de Instagram. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de X. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informations