Tutoriel Analyse spectrale de Fourier
Ce tutoriel traite des possibilité d'analyse spectrale de Fourier de FlexPro pour les cas où vous voulez caractériser des composantes de très faible puissance dans des signaux stationnaires à sens large et où des estimations spectrales à faible variance sont souhaitées.
Un signal d'essai approprié
Pour ce tutoriel, nous utiliserons un signal qui contient quatre sinusoïdes de référence de puissance égale sur la plage de Nyquist et trois sinusoïdes de faible puissance placées entre elles. Les composantes de faible puissance seront de -40 dB, -50 dB, et -60 dB en dessous des sinusoïdes de référence. Un bruit blanc sera ensuite ajouté de manière à obtenir un plancher de bruit à environ -75 dB. L'objet de ce test est l'estimation précise de la fréquence et de la puissance de ces trois composants de faible puissance. Un objectif secondaire sera la récupération des informations de phase pour ces composants.
Les quatre sinusoïdes de référence et les trois sinusoïdes de puissance inférieure sont définies comme suit :
1.0*sin(2π*x*1005+p/2)+ (0dB)
1.0*sin(2π*x*2005+p/2)+ (0dB)
1.0*sin(2π*x*3005+p/2)+ (0dB)
1.0*sin(2π*x*4005+p/2)+ (0dB)
0.01*sin(2π*x*1505+p/2)+ (-40dB)
0.003162*sin(2π*x*2505+3p/2)+ (-50dB)
0.001*sin(2π*x*3505+p) (-60dB)
Les valeurs x (temps) varient de 0 à 0,1 avec un incrément de 0,0001 échantillon. La fréquence de Nyquist est donc de 5000 (la moitié de la fréquence d'échantillonnage de 10000). Les quatre sinusoïdes de référence couvrent la plage de Nyquist. La première sinusoïde de faible puissance (-40 dB) a 1% de l'amplitude et 0,01% de la puissance de l'une des sinusoïdes de référence. La sinusoïde de faible puissance suivante (-50 dB) a 0,001% de la puissance des références. La dernière des sinusoïdes de test (-60 dB) n'a que 0,1% de l'amplitude et 0,0001% de la puissance des sinusoïdes de référence. Un bruit gaussien à 0,15% a été ajouté pour créer un bruit blanc de fond à environ -75 dB. Il devrait donc être possible de résoudre même la composante de -60 dB avec une analyse spectrale bien conçue.
Sélectionnez la commande Fichier > Ouvrir Base de données projet et ouvrez la base de données projet C:\Users\Public\Documents\Weisang\FlexPro\2021\Exemples\Tutoriels\Analyse spectrale.fpd ou C:>Utilisateurs>Public>Documents Public>Weisang>FlexPro>2021>Exemples>Tutoriels>Analyse spectrale.fpd. Ouvrez le dossier Tutoriels et son sous-dossier Analyse spectrale de Fourier, puis double-cliquez pour ouvrir le graphique 2D appelé Données.
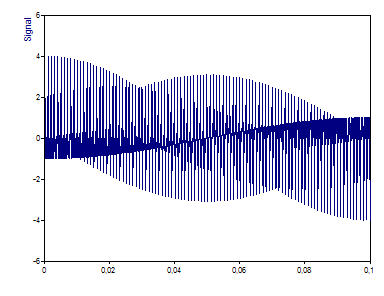
C'est un graphique du signal. Il y a 1001 valeurs à virgule flottante.
Le spectre de Fourier non fenêtré
Pour l'analyse spectrale de Fourier à haute dynamique, des fenêtres d'observation de données sont presque toujours utilisées. Afin de comprendre pourquoi, nous allons d'abord explorer une FFT de base ou non fenêtrée.
Fermez le graphique et mettez en évidence l'ensemble de données Signal.
Cliquez sur Insérer[Analyses] > Assistant d'analyse.
Sélectionnez les analyses de Fourier sous Analyses spectrales. Ensuite, sélectionnez Spectre de Fourier. Cliquez sur Suivant.
L'étape 2 de l'assistant d'analyse contient une boîte de dialogue interactive où plusieurs procédures peuvent être optimisées et comparées afin d'obtenir la meilleure analyse possible. Nous allons commencer par explorer le spectre de Fourier non fenêtré.
Notez que pour la procédure spectrale, l'option Spectre de Fourier est cochée. Bien que la procédure spectrale ait été sélectionnée à l'étape 1 de l'assistant d'analyse, elle peut être modifiée à l'étape 2.
Sélectionnez pour le Type de Spectre la valeur dB normalisée.
Cela normalise le plus grand pic spectral à 0 dB. Tous les autres pics auront une valeur négative. Un pic à -3 dB aurait la moitié de la puissance du pic à 0 dB, et un pic à -6 dB aurait la moitié de l'amplitude.
Pour le type de fenêtre, sélectionnez Rectangulaire -13dB W=1.
Dans le module d'analyse spectrale de FlexPro, toutes les fenêtre d'observation de données à largeur fixe (non ajustable) sont répertoriés par leur nom, l'atténuation du lobe latéral en dB, et la largeur du pic du domaine de Fourier unilatéral. Une fenêtre rectangulaire est identique à l'absence de fenêtrage, car tous les éléments de données sont multipliés par l'unité.
Assurez-vous que la longueur de la FFT est réglée sur la longueur des données ou sur 1001.
Le champ d'information Zero Padding indique qu'il n'y a pas eu de rajout de zéro (zero padding).
Sélectionnez Nombre maximal de pics sous Options et entrez la valeur 7.
L'assistant d'analyse génère automatiquement des informations sur les pics spectraux. Si cette option est réglée sur 7, les sept pics de puissance les plus élevés seront émis. Notez qu'il est également possible de définir un seuil en dB en dessous du pic le plus important. Pour cet ensemble de données, nous aurions pu tout aussi bien fixer un seuil de -65 dB.
Définissez maintenant le % de limite critique du bruit blanc à Aucun.
Plus tard dans ce tutoriel, nous appliquerons le test de limite critique à ce signal.
Si aucune étiquette n'est visible au-dessus des pics, cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes d'amplitude apparaissent.
Vous pouvez basculer entre plusieurs états. Vous pouvez passer d'un état d'étiquetage à l'autre, en affichant la composante y du spectre (ici, elle est normalisée en dB), la composante x (toujours les fréquences), ou aucune information sur les pics.
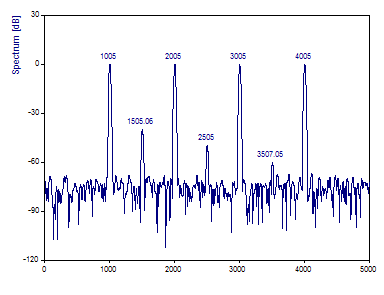
Le tracé de Fourier dans l'assistant d'analyse devrait être le suivant :
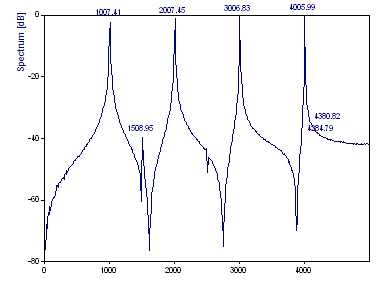
Le calcul de la FFT utilise l'algorithme FFT le plus rapide disponible qui transforme exactement les données. Dans ce cas, l'algorithme Prime Factor FFT est utilisé car il s'agit de la procédure FlexPro FFT la plus rapide qui traite exactement la taille des données de 1001. Le spectre de Fourier qui est produit permet de détecter facilement les quatre pics de référence. Le pic de -40 dB est observé. Il n'y a qu'un soupçon du pic de -50 dB et aucune trace du pic de -60 dB. Même si FlexPro utilise une interpolation de bin spline cubique pour affiner les fréquences de crête FFT, les fréquences de référence de 1005, 2005, 3005 et 4005 ne sont pas exactement récupérées.
Notez que les quatre références sont constituées de pics qui ont des formes sensiblement différentes. Les pics spectraux deviennent plus nets à mesure que les fréquences augmentent. Il ne s'agit pas d'un produit de la fréquence, mais plutôt d'une fuite spectrale vers les bacs adjacents. Plus une harmonique est centrée dans une case de fréquence spectrale, plus la réponse en fréquence de la FFT sera nette.
Sélectionnez le tracé supérieur et cliquez sur le bouton Activer les curseurs. Placez le curseur sur le premier pic.
Observez que la fréquence réelle de 1005 du premier pic doit être prise en compte par les bins FFT de fréquences 999 et 1009. La fréquence réelle du quatrième pic, 4005, peut en grande partie être prise en compte par une case FFT de fréquence 4006. Ce n'est que lorsqu'une fréquence se trouve exactement au centre d'une case qu'une harmonique peut être entièrement représentée par un seul canal FFT.
Cliquez à nouveau sur Activer les curseurs pour désactiver le curseur, puis modifiez la longueur de la FFT à 8192.
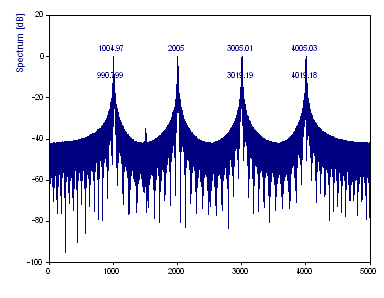
Cela augmente la taille de la FFT en utilisant le rajout de zéro (zero padding). Il y a maintenant environ huit fois plus de fréquences dans le spectre. Les fréquences bin-interpolées des références sont maintenant déterminées avec précision, mais les trois composantes de faible puissance sont perdues dans la ligne de base. Les fuites spectrales augmentent car le rajout de zéro (zero padding) introduit une discontinuité dans le flux de données.
Entrez 2000 dans le champ Longueur FFT. Pour déclencher la mise à jour, quittez le champ d'édition en appuyant sur la touche Tabulation.
Cela produit une FFT espacée à des intervalles de 5 Hz exactement. Les fréquences des sept sinusoïdes sont maintenant exactement au centre d'un bin de la FFT :
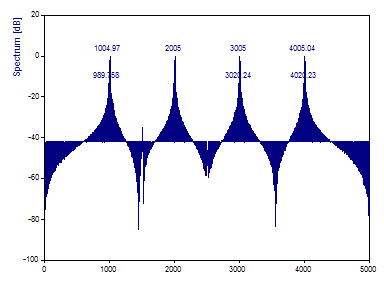
Les pics spectraux sont maintenant des fonctions impulsionnelles, mais la fuite spectrale introduite par le rajout de zéro (zero padding) est suffisante pour masquer les trois composantes de puissance inférieure. Il n'est pas possible de résoudre les composantes de faible puissance sans utiliser une fenêtre d'observation des données.
Spectres de Fourier fenêtrés
Une fenêtre d'observation de données ramène l'amplitude des valeurs des données à zéro à chaque extrémité du flux de données. Bien que cela augmente l'influence des données au centre du flux de données et diminue l'influence des données près des limites, cela élimine la discontinuité aux limites des données. Si les données devaient être considérées dans un format enveloppant, une continuité serait observée là où les deux extrémités se rencontrent.
L'influence de l'ajout d'une fenêtre d'observation de données n'est pas neutre dans le domaine de Fourier. La fenêtre de données aura une réponse en fréquence qui élargit tout pic spectral, réduisant ainsi sa résolution. Les harmoniques de faible puissance sont également introduites. L'avantage est une réduction spectaculaire des fuites spectrales, ce qui permet d'utiliser n'importe quelle mesure de rajout de zéro (zero padding).
Dans FlexPro, une normalisation de la puissance est effectuée chaque fois qu'une fenêtre de données est utilisée. La puissance d'un spectre de Fourier fenêtré est identique à la puissance de son homologue non fenêtré. D'autre part, même avec cette conservation de la puissance, la hauteur des pics spectraux présentera une certaine atténuation en raison du fenêtrage. Lorsqu'une fenêtre d'observation de données est utilisée, il est toujours possible de juger de la puissance relative en utilisant une échelle de dB normalisée, mais il n'est plus possible de lire directement les amplitudes ou les puissances absolues en utilisant les hauteurs des pics spectraux.
Changez le type de fenêtre en Cos4 Blackman-Harris -92dB W=4 et réglez la longueur de la FFT à 8192.
Cliquez sur Basculer les étiquettes pour afficher les magnitudes spectrales comme étiquettes.
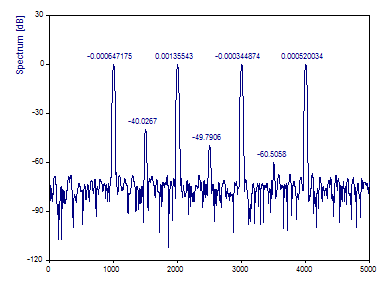
Cette fenêtre de Blackman-Harris est populaire pour l'analyse de Fourier à haute dynamique. Les quatre pics de référence sont cartographiés avec précision, tant pour la fréquence que pour la puissance. Les trois pics de faible puissance sont également bien caractérisés à la fois pour la fréquence et la puissance.
Notez qu'un pic exact de 0 dB n'est pas présent. La normalisation à zéro dB se produit sur les valeurs spectrales réelles. Les valeurs de crête indiquées sont interpolées par bin et, de ce fait, la crête de puissance la plus élevée sera généralement légèrement supérieure à 0 dB.
Fenêtre d'observation des données
La sélection d'une fenêtre d'observation de données appropriée demande de la pratique. Dans FlexPro, il existe vingt fenêtres de propriétés fixes, et neuf dont les propriétés varient en fonction d'un paramètre réglable.
La largeur du lobe principal indiquée dans la liste de sélection comme paramètre W est directement liée à la résolution en fréquence. Une fenêtre dont la largeur du lobe principal est de 3 n'aura qu'un tiers de la résolution en fréquence d'un spectre de Fourier non fenêtré. La valeur du lobe secondaire, également indiquée dans la liste de sélection, est la mesure en dB dans laquelle la plus grande crête du lobe secondaire est inférieure à la crête primaire. Plus la valeur du lobe latéral est élevée, plus la probabilité de résoudre un pic de faible puissance à proximité d'une composante de plus forte puissance est grande. Un autre facteur de sélection des fenêtres est la valeur de Rolloff. Plus l'atténuation est importante, plus les chances de résoudre les composantes de faible puissance éloignées du pic spectral primaire sont grandes. La valeur du lobe secondaire est une mesure de la fuite spectrale qui se produit et la valeur de l'atténuation spécifie comment elle est distribuée sur le spectre.
Le principal compromis est la résolution par rapport à la gamme dynamique, et celle-ci est déterminée par la largeur du lobe principal. Le compromis secondaire est la résolution des pics adjacents par rapport aux pics très espacés. Ceci est déterminé par les caractéristiques du lobe latéral et de l'atténuation.
La fenêtre de Tchebyshev produit le pic spectral le plus net pour un niveau de lobe latéral donné. Il s'agit d'une excellente fenêtre d'observation pour la résolution de composantes très rapprochées de différents niveaux de puissance. La fenêtre Cosine Maximum Rolloff produit la décroissance cosinusoïdale la plus rapide dans le domaine des fréquences, ce qui permet de résoudre des pics de très faible puissance situés à une certaine distance des pics spectraux primaires. La fenêtre de Kaiser-Bessel est une très bonne fenêtre réglable qui offre un compromis efficace entre les deux extrêmes.
La fenêtre Flattop représente une caractéristique unique. Cette fenêtre a une largeur maximale du lobe principal de 5, offrant ainsi une résolution spectrale relativement faible ; cependant, le maximum du lobe principal a presque la même valeur dans la bande complète d'une ligne de fréquence à sa voisine à gauche et à droite. Le maximum du lobe principal présente donc un pic large, mais plat. Cette fenêtre est particulièrement adaptée à la mesure des puissances ou des amplitudes des composantes de signaux à bande étroite, c'est-à-dire des pics individuels dans un spectre. Grâce au type particulier de maximum du lobe principal, la hauteur d'un pic est en fait indépendante de son emplacement entre deux lignes de fréquence.
Niveaux de signification
FlexPro propose des limites critiques basées sur les pics pour déterminer si le pic d'un signal est statistiquement significatif ou non. La référence est un bruit blanc (normalement distribué). Une limite critique de 95 % est le niveau où, dans seulement 1 des 20 signaux de bruit aléatoires distincts, le plus grand pic présent atteindrait cette hauteur strictement par hasard. Une limite critique de 99,9 % correspond à un niveau où le pic le plus important n'atteindrait cette hauteur que dans un seul ensemble de bruits aléatoires sur 1000.
Les limites critiques de FlexPro sont basées sur des essais approfondis de Monte Carlo utilisant les algorithmes et les ajustements réels du programme. Dans ce cas, des modèles de limites critiques distincts sont utilisés pour chacune des fenêtres de données de FlexPro. Pour les fenêtres ajustables, des modèles de surface 3D sont utilisés. Comme cette approche intègre l'atténuation de la hauteur des pics qui se produit lorsque des fenêtres de données sont utilisées, les limites critiques sont précises pour tous les n, toutes les fenêtres de données et tous les paramètres ajustables des fenêtres de données.
Changez la limite critique du bruit blanc à 99,9%.
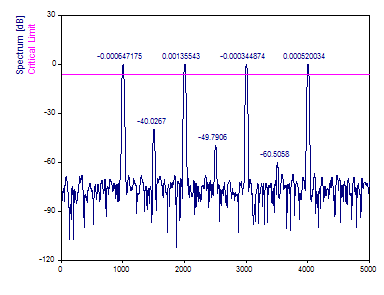
Dans cet ensemble de données, le pic le plus important s'avère être significatif avec un taux de confiance de 99,9%. Ce test compare uniquement la caractéristique spectrale de puissance la plus élevée au bruit gaussien. Aucune déduction ne peut être faite par rapport à un autre pic.
Références
À des fins de comparaison, nous conserverons ce graphique comme référence.
Pour ce faire, cliquez sur Définir la référence.
La référence remplace le tracé des données. Notez que les limites critiques et les pics ne sont pas inclus dans les références.
Analyse spectrale à faible variance
Nous allons maintenant explorer les méthodes spectrales de FlexPro pour les cas où des estimations de puissance spectrale à faible variance sont nécessaires. On suppose ici que la précision des mesures de puissance est la considération principale.
Réduction de la variance dans les mesures spectrales
La variance d'une FFT ne diminue pas lorsque la longueur des données augmente. Au lieu de cela, la variance est une constante dont la racine carrée (écart-type) est approximativement égale à la puissance moyenne présente dans le signal. Pour réduire la variance des estimations spectrales basées sur la FFT, des techniques de moyenne d'ensemble et de fenêtre d'observation orthogonale sont utilisées.
Périodogramme (spectre de Fourier segmenté et superposé)
Il existe deux procédures de Fourier dans FlexPro qui peuvent être utilisées pour produire des estimations spectrales à variance réduite. Le premier d'entre eux est le "périodogramme". Pour une série de données stationnaire, chaque sous-ensemble de la séquence complète de données doit avoir les mêmes caractéristiques spectrales. Il est donc possible d'additionner une série de FFT afin de produire une estimation de variance plus faible. Les FFT sont effectuées dans une fenêtre glissante (une taille de segment plus petite) qui est déplacée sur la séquence de données avec une mesure de chevauchement spécifiée. La taille réduite de la FFT entraîne une diminution de la résolution. La résolution est sacrifiée en échange d'une moindre variabilité dans les estimations spectrales finales.
Pour la procédure spectrale, sélectionnez l'option Périodogramme. Pour le type de spectre, continuez à utiliser le paramètre dB normalisé. Sélectionnez la fenêtre Tchebychev et réglez la largeur de Fourier unilatérale(Réglage de la fenêtre ) sur 4,0. Si nécessaire, réglez la longueur du segment sur la valeur par défaut de longueur de données/4. Définissez la longueur de la FFT à 4096 et le % de chevauchement à 90. Si aucune étiquette n'est visible au-dessus des pics, cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes d'amplitude apparaissent.
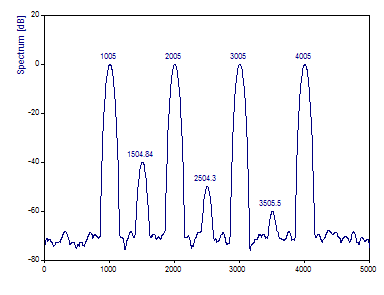
Cliquez sur Basculer les étiquettes pour afficher les densités spectrales en dB.
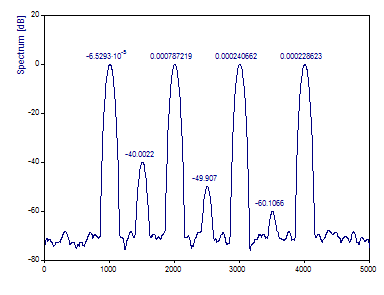
Avec la longueur de segment par défaut n/4 (250) et un chevauchement de 90%, il y a 31 segments discrets qui sont combinés pour produire un spectre à faible variance. Comme la longueur du segment ne représente qu'un quart de la longueur du flux de données complet, la résolution dans le domaine des fréquences est proportionnellement réduite. C'est pourquoi les pics sont beaucoup plus larges dans le périodogramme. Cependant, il y a 31 spectres de Fourier individuels qui sont additionnés pour produire le périodogramme global. Pour cette raison, les trois pics de faible puissance sont caractérisés de manière plus précise pour la puissance.
La fenêtre de Tchebyshev a été utilisée ici parce qu'il y a un plancher de bruit blanc constant sur toutes les fréquences. Il n'y a pas d'avantage dans une fenêtre avec des caractéristiques de rolloff significatives. Si un bruit rouge (bruit qui diminue avec l'augmentation de la fréquence) avait été présent, une fenêtre avec un rolloff très élevé, comme le rolloff Beta ou Cosine Maximum, aurait été un meilleur choix.
L'optimisation de la taille et du chevauchement des segments n'est généralement pas une tâche agréable. En général, un grand nombre de segments ne permet pas d'améliorer sensiblement la variance. En général, la réduction de la variance est faible au-delà d'un chevauchement de 50 à 70 %, que l'on utilise ou non le fenêtrage des données.
Amplitudes et fenêtre d'observation de données
C'est un bon endroit pour observer l'impact sur les amplitudes lorsqu'une fenêtre d'observation de données est utilisée.
Changez le Type de fenêtre en Rectangulaire -13dB W=1 (pas de fenêtrage), la Normalisation en Aucun, et changez le Type de spectre en Amplitude.
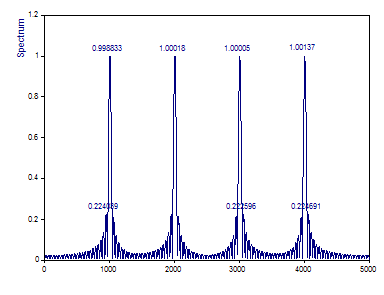
Notez que les amplitudes des quatre sinusoïdes de référence, chacune de 1,0, sont récupérées de manière très précise en raison de leur fort chevauchement.
Changez le type de fenêtre en Cos2 Hamming -43dB W=2.
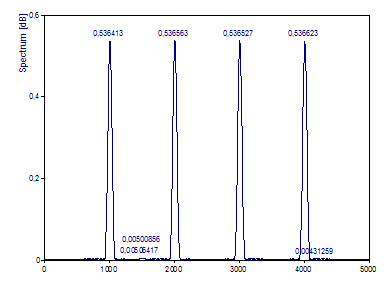
La fenêtre de Hamming est la fenêtre de la série de cosinus à lobe latéral minimal pour une largeur de Fourier unilatérale de 2. Notez que les amplitudes dans le pic ont été réduites d'environ 50%. Si le spectre est constitué de pics séparés, la réduction ne dépend que de la fonction fenêtre sélectionnée et peut être compensée très facilement.
changez la Normalisation en Amplitude.
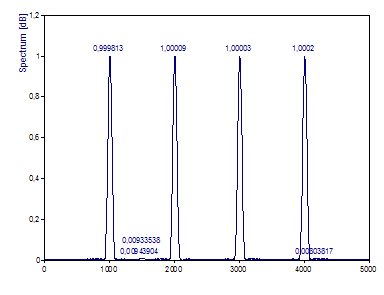
Les amplitudes des pics sont exactement les mêmes que les oscillations de référence du signal. La normalisation de l'amplitude utilise le gain de la fonction fenêtre sélectionnée comme facteur de normalisation, c'est-à-dire la somme des valeurs au carré de la fonction fenêtre divisée par leur nombre. Veuillez noter que ce type de normalisation ne garantit pas que la puissance totale du spectre soit égale à celle du signal temporel. Dans les cas où cela est demandé, le type de normalisation Puissance est disponible.
Optimisation du Périodogramme
Changez le type de fenêtre en Cos3 Sidelobe minimum -71dB W=3.
L'amortissement des lobes latéraux de -71 dB indiqué dans la description de cette fenêtre suggère qu'il devrait maintenant y avoir une gamme dynamique suffisante pour récupérer les trois pics de faible puissance.
Changez le Type de Spectre en dB normalisé.
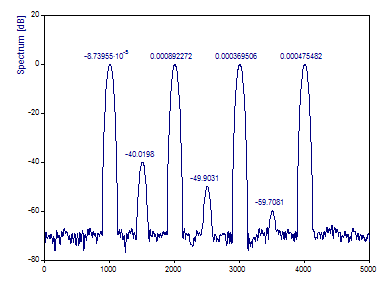
Notez que les trois composantes à bande étroite de faible puissance sont effectivement résolues en utilisant cette fenêtre d'observation de données. Les pics spectraux sont également plus nets avec cette fenêtre de largeur 3 que dans la fenêtre d'observation de Tchebyshev de largeur 4 que nous avons d'abord évalué. Bien que cela n'ait pas été important dans ce cas, il peut y avoir des cas où des caractéristiques spectrales très rapprochées nécessitent l'utilisation d'une fenêtre dont le dB du lobe latéral est juste inférieur à celui du plancher de bruit des données. Notez que les fenêtres ajustables sont continues, et qu'il est possible de définir toute largeur de Fourier fractionnelle souhaitée.
Changez le type de fenêtre en Tchebyshev et définissez la largeur de Fourier unilatérale, l'ajustement de la fenêtre à 2,9.
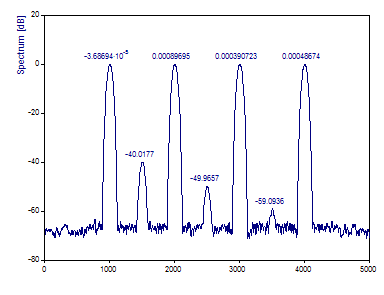
Cela représente une fenêtre d'observation de données proche de l'optimum pour minimiser la largeur des pics spectraux. Les pics ont la largeur minimale permettant de résoudre les composantes de puissance les plus faibles au-dessus du plancher de bruit. Cependant, ce ne sont pas nécessairement les réglages optimaux pour le périodogramme. Si une partie de l'amélioration de la variance est sacrifiée, un spectre beaucoup plus net est possible.
Sélectionnez 500 dans la liste déroulante Longueur du segment et maintenez le % de chevauchement à 90 .
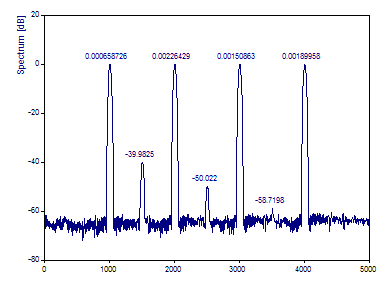
Lorsque ces paramètres sont utilisés, 11 spectres de Fourier de demi-longueur sont utilisés pour générer le périodogramme. Notez que les pics spectraux sont beaucoup plus nets. La plus grande variance est également évidente dans le plancher plus bruyant du spectre et dans la très faible récupération de la composante de plus faible puissance.
Analyse Spectrale Multitaper
La deuxième option de Fourier dans FlexPro pour générer des spectres à variance réduite est la procédure multitaper. Dans une procédure multitaper, un ensemble de fenêtres d'observation orthogonales est appliqué aux données et le spectre de chacun d'elle est moyenné d'une manière ou d'une autre pour produire un spectre composite. Contrairement à l'approche segmentée et superposée qui n'utilise qu'une partie du flux de données pour chaque spectre individuel, une procédure multitaper utilise le flux de données complet pour chaque fenêtre d'observation.
Une procédure multitaper est quelque peu similaire au calcul de la moyenne des spectres provenant de diverses fenêtres d'observation de données. Dans ce cas, il y aurait une certaine redondance puisque les différentes fenêtres d'observation sont fortement corrélées (toutes ont une forme de pic très commune). Contrairement aux fenêtres d'observation de données classiques, les fenêtre d'observation orthogonales utilisées pour produire un spectre multitaper ne sont pas corrélées. Seule la première des fenêtres d'observation de données a la forme traditionnelle.
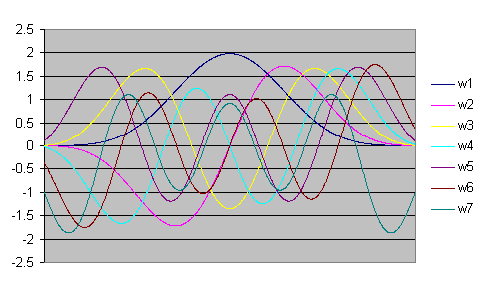
Les spectres des différentes fenêtres d'observation ne produisent pas un pic central commun pour une composante harmonique. Seul la première fenêtre d'observation produit un pic central à la fréquence harmonique de la composante. Les autres fenêtres d'observation produisent des pics spectraux dont la fréquence est légèrement décalée vers le haut ou vers le bas. Chacun de ces spectres contribue à une enveloppe spectrale globale pour chaque composant.
Les avantages de l'analyse multitaper sont qu'aucune résolution de Fourier n'est sacrifiée et qu'il n'y a pas de perte d'informations aux extrémités des données. Alors que l'information proche des limites est effectivement perdue avec la première fenêtre d'observation, elle est incluse et même accentuée dans les fenêtres d'observation suivantes. L'enveloppe spectrale associée à chaque composant permet de déterminer facilement la puissance relative. L'inconvénient est que l'enveloppe spectrale associée à chaque composante n'offre pas d'emblée une résolution fréquentielle précise.
La procédure multitaper effectue toujours une normalisation de la puissance pour le spectre résultant. Ainsi, en sélectionnant Aucun et Puissance dans la liste Normalisation, vous obtenez le même résultat. Le type de normalisation Amplitude peut être utilisé de la même manière que pour le périodogramme pour compenser l'atténuation de l'amplitude des pics dans le spectre. Les facteurs de normalisation ont été déterminés empiriquement en fonction du nombre de fenêtres et de la largeur des fenêtres.
Sélectionnez le Spectre Multitaper comme Procédure spectrale et sélectionnez le type de spectre en dB normalisé. Définissez la largeur de Fourier unilatérale(ajustement de la fenêtre) à 3,0. Pour le Nombre de fenêtres DPSS, entrez maximum ou 5. Définissez la longueur de la FFT à 4096. Cliquez sur Basculer les étiquettes jusqu'à ce que les fréquences soient affichées au-dessus des pics.
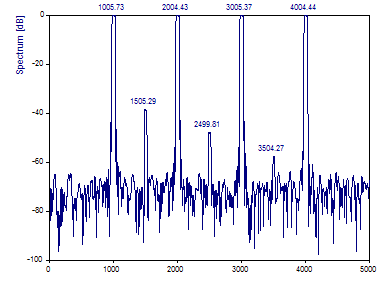
Notez les pics spectraux en forme de « table-top », caractéristiques d'un spectre multitaper. Cette forme permet de discerner visuellement la puissance spectrale relative, mais il est difficile de localiser la fréquence centrale de l'enveloppe qui définit chaque pic. FlexPro utilise les emplacements des crêtes dans le spectre du rapport F pour attribuer les fréquences de crête. Les valeurs F sont une mesure de signification et ne sont pas directement liées à la variance.
Cliquez sur Basculer les étiquettes pour afficher les densités spectrales en dB.
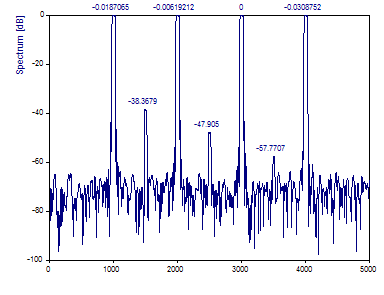
Il est à noter que, contrairement au périodogramme, le calcul de la moyenne des spectres des fenêtres d'observation orthogonales ne permet pas d'obtenir un bruit de fond plus lisse.
Comme l'enveloppe multitaper n'a pas de pics nets bien définis, le maximum dans les spectres ne peut pas être déterminé avec une grande précision. C'est une des raisons possibles pour lesquelles les trois pics de faible puissance sont décalés de +2 dB dans le spectre normalisé.
Une mise en garde dans l'analyse spectrale multitaper concerne l'utilisation du nombre maximum de fenêtres d'observation supportées. Pour une largeur unilatérale de Fourier de 3,0, FlexPro prend en charge jusqu'à 5 cônes. Pour une largeur de 4,0, on peut utiliser jusqu'à 7 cônes DPSS. La gamme dynamique de chaque tapers DPSS diminue au fur et à mesure que la séquence progresse. La première fenêtre d'observation DPSS, w1 dans le graphique DPSS, est une excellente fenêtre d'observation de données et il offre la meilleure gamme dynamique de la séquence (il s'agit de la fenêtre ajustable Slepian dans les procédures Fourier et Periodogramme). Chaque fenêtre d'observation suivante de la séquence DPSS offre une gamme dynamique réduite. Il est souvent préférable, lorsqu'une large gamme dynamique est souhaitée, d'exclure la dernière ou les deux dernière fenêtre d'observation de la séquence. Par exemple, pour un réglage de largeur de Fourier 3, un total de 3 ou 4 cônes peut être le meilleur choix. Pour un spectre de largeur de Fourier 4, 5 tapers peuvent donner les meilleurs résultats.
Changez le nombre de fenêtres DPSS en 3.
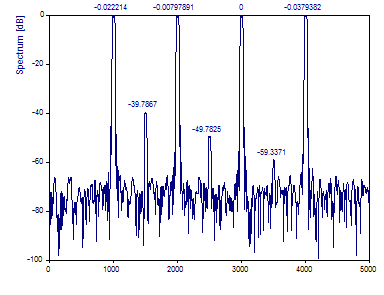
Notez que les pics spectraux sont sensiblement plus précis.
Atténuation Amplitude Multitaper
Modifiez le nombre de fenêtres DPSS à 5 ou au maximum. Définissez la Normalisation à Puissance et changez le Type de Spectre sur Amplitude.
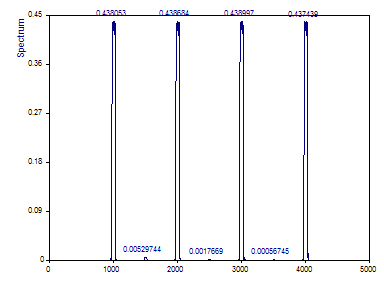
Pour le périodogramme avec une fenêtre d'observation de données de largeur de Fourier 3, l'atténuation de l'amplitude était d'environ 24% (76% de l'amplitude réelle était présente dans le canal de crête). Pour le multitapis avec une largeur de Fourier de 3, l'atténuation est beaucoup plus importante : 56 % (seulement 44 % de l'amplitude réelle est évidente dans le plateau de l'enveloppe spectrale du multitapis).
Changez le nombre de fenêtres DPSS en 3.
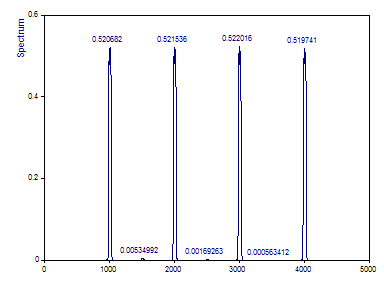
L'atténuation spectrale n'est pas seulement une fonction de la largeur de Fourier de l'analyse multitaper, mais elle est aussi fortement influencée par le nombre de tapers utilisés dans la séquence. Dans le cas où seuls les trois premiers cônes Slepian sont utilisés, l'atténuation de l'amplitude est d'environ 48%, contre 56% lorsque les 5 cônes maximum sont utilisés.
Sélection du type de normalisation amplitude compense parfaitement l'atténuation.
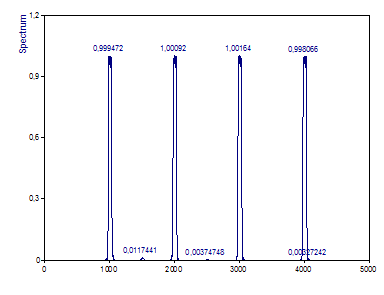
Sélection de la meilleure méthode pour l'analyse de Fourier à faible variance et à gamme dynamique élevée
(1) Assurez-vous que les données sont stationnaires au sens large (WSS) sur toute la longueur du signal. Utilisez les analyses STFT ou CWT pour vous assurer que l'information spectrale ne varie pas dans l'échantillon. Une fenêtre d'observation des données diminuera considérablement l'influence des informations situées aux deux extrémités du flux de données. Cela ne doit être fait que si l'influence des données des périodes les plus anciennes et les plus récentes de l'échantillon peut être minimisée.
(2) Pour réduire les fuites spectrales et obtenir une analyse de Fourier à haute dynamique, une approche de fenêtre d'observation des données sera généralement nécessaire. Il faut donc s'attendre à ce que les amplitudes et les puissances spectrales soient atténuées et ne puissent être lues directement à partir des pics spectraux. Pour évaluer avec précision les puissances et les amplitudes, utilisez le type de normalisation de l'amplitude.
(3) Si la longueur des données est très grande, l'analyse commence par une haute résolution dans le domaine fréquentiel. Une partie de cette réduction peut être échangée contre la réduction de la variance offerte par le périodogramme.
(4) Si la longueur des données est limitée et que le but de l'analyse est d'estimer avec précision à la fois les fréquences et la puissance, il peut être nécessaire d'utiliser le spectre de Fourier unique. Les pics spectraux auront la résolution maximale possible, mais la variance sera plus élevée car les pics de bruit aléatoire seront plus présents dans les données. L'option Spectre de Fourier est également le meilleur moyen de tester la différence entre un signal donné et le bruit, car ses analyses fenêtrées offrent des limites critiques de bruit blanc là où celles-ci ne sont disponibles dans le périodogramme que pour le cas non fenêtré.
(5) De même, si la longueur des données est limitée et que le but de l'analyse est principalement de caractériser avec précision la puissance, et surtout s'il est essentiel d'utiliser toute l'information contenue dans les données, y compris celle qui se trouve près des limites, le spectre multitaper est probablement le meilleur choix.
(6) Ces trois analyses sont applicables à de nombreux problèmes d'analyse spectrale. FlexPro simplifie le choix de la méthode en plaçant les trois algorithmes dans une seule option d'analyse de Fourier. Utilisez l'option Référence pour comparer côte à côte les différentes procédures. Dans certains cas, la meilleure analyse peut résulter de l'utilisation des trois méthodes.
Étape 3 - Options de résultat
Afin d'explorer les objets que l'assistant d'analyse de FlexPro peut créer automatiquement, nous allons générer un spectre de Fourier.
Pour la procédure spectrale, sélectionnez Spectre de Fourier. Pour le Type de spectre, sélectionnez dB normalisé. Pour le type de fenêtre, sélectionnez Kaiser-Bessel et pour l'ajustement de la fenêtre, entrez 3.0. Définissez la longueur de la FFT à 8192. Sélectionnez l'option Maximum peak count et entrez 7. Définissez maintenant le % de limite critique du bruit blanc à 99. Cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes de fréquence soient affichées. Cliquez sur Suivant. À l'étape 3, cochez les trois options, puis cliquez sur Terminer.
Huit objets au total sont créés dans la base de données projet FlexPro.
"Spectre" est l'objet d'analyse. Il s'agit de l'objet qui effectue l'analyse spectrale. Un double clic sur cet objet ouvre l'objet d'analyse créé par l'assistant.
"Limite critique" est l'objet de la formule permettant de générer les limites critiques utilisées dans le tracé.
"Pics" est l'objet de la formule permettant de générer les informations sur les pics affichés dans le tracé.
"Analyse harmonique" est l'objet formule qui génère le rapport d'analyse harmonique.
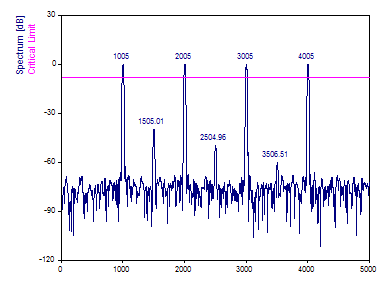
"Spectre" est le tracé du spectre de Fourier généré par l'assistant. Il utilise les objets Spectre, Limite critique et Pics :
"Données" est un graphique des données originales du domaine temporel.
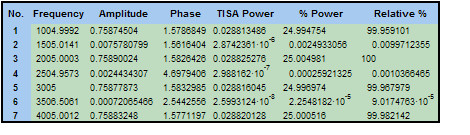
"Analyse harmonique" est un tableau d'informations spectrales pour les sept composantes à bande étroite spécifiées par le nombre maximal de pics de 7. Le tableau affiche la fréquence, l'amplitude, la phase et la puissance de l'amplitude intégrée dans le temps². Le "% puissance" additionne les composants à 100%, le "% relatif" attribue 100% au composant ayant la plus grande puissance.
"Fourier" est un document qui contient les tracés spectraux et les données.
Analyse spectrale pour données non équidistantes
Nous allons maintenant traiter les possibilités d'analyse spectrale de Fourier de FlexPro lorsque les données sont espacées de façon non équidistantes. L'accent sera mis sur une procédure de Fourier conçue pour les données qui n'ont pas été échantillonnées uniformément.
Vous pouvez ignorer le reste de ce tutoriel si vous travaillez toujours avec des données uniformément échantillonnées.
Ouvrez le dossier Tutoriels dans la base de données projet d'exemple et le sous-dossier Fourier inégal, puis double-cliquez pour ouvrir le graphique 2D appelé Données .
C'est un graphique du signal. Il y a 1000 valeurs à virgule flottante. Les valeurs x sont croissantes dans la plage de 0 à 10, mais elles ne sont pas uniformément espacées. C'est le pire scénario pour l'algorithme de Fourier à espacement irrégulier.
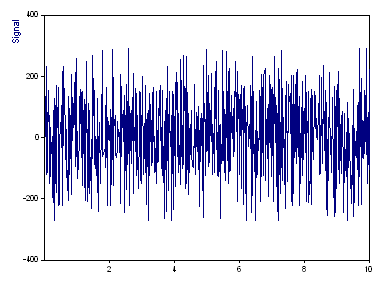
Cet ensemble de données contient trois pics spectraux, l'un à une fréquence de 30 (amplitude 100, phase 3π/2), un autre à une fréquence de 70 (amplitude 100, phase π), et un troisième pic à la fréquence de 120 (amplitude 100, phase π/2). La fréquence moyenne de Nyquist est de 50,05. Il y a donc deux pics au-delà de la limite moyenne de Nyquist.
Une différence importante entre les données échantillonnées de manière irrégulière et les données échantillonnées de manière uniforme est que les informations situées au-delà de la limite moyenne de Nyquist ne sont pas automatiquement aliasées vers des fréquences plus basses. Il est donc possible d'extraire des informations au-delà de cette fréquence moyenne de Nyquist puisque certaines des données sont plus rapprochées et supportent une fréquence de Nyquist "locale" beaucoup plus élevée.
De même, il y aura des points très espacés dont la fréquence de Nyquist locale est plus petite que la moyenne générale. L'information dans la plage moyenne de Nyquist est donc incomplète.
Périodogramme Lomb-Scargle
Le périodogramme de Lomb-Scargle est un algorithme qui génère spécifiquement un spectre de Fourier dans le cas où les données ne sont pas uniformément espacées.
Fermez le graphique et mettez en évidence l'ensemble de données Signal.
Cliquez sur Insérer[Analyses] > Assistant d'analyse. Sélectionnez Analyses des données inégalement espacées dans Analyses spectrales, puis sélectionnez Fourier des données inégales. Cliquez sur Suivant.
Dans l'étape 2 de l'assistant d'analyse, nous allons commencer par explorer le spectre de Fourier non fenêtré avec une fréquence maximale égale à celle de la moyenne de Nyquist.
Pour le Type de spectre, sélectionnez dB normalisé. Pour le type de fenêtre, sélectionnez Rectangulaire -13dB W=1 (pas de fenêtrage). Définissez le nombre de fréquences à 1024 et le multiple de Nyquist à 1,0. Cochez Nombre maximal de pics et entrez 3. Le% de limite critique du bruit blanc est réglé sur 99.
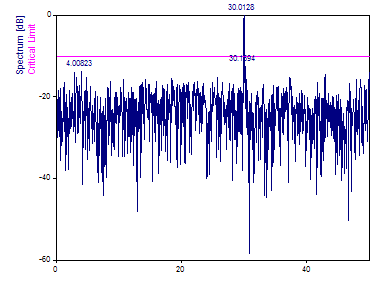
Seul le pic de la fréquence 30.0 est trouvé car les pics aux fréquences 70.0 et 120.0 sont au-delà de la valeur moyenne de Nyquist.
Le pic le plus important est supérieur à la limite critique de 99 %, ce qui signifie qu'il y a moins d'une probabilité sur 100 que cette caractéristique spectrale la plus importante soit le fruit du hasard, par le biais du bruit aléatoire. Une autre façon de le dire est que sur cent ensembles de données de bruit blanc ayant une variance équivalente, on ne s'attendrait pas à ce que l'un d'entre eux présente un pic de cette ampleur.
Notez également que cet algorithme ne génère pas de valeur de fréquence 0.
Extension du spectre au-delà de la fréquence moyenne de Nyquist
Changez le multiple de Nyquist à 2.0. Pour conserver la même densité de caractéristiques spectrales, augmentez le nombre de fréquences à 2048.
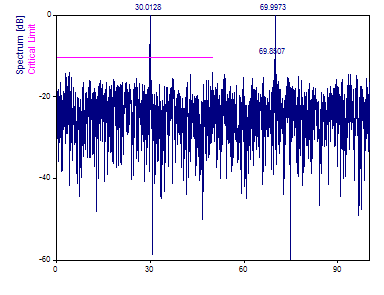
Notez que le spectre récupère maintenant les composantes de fréquence 30 et 70.
Changez le multiple de Nyquist à 4.0. Pour conserver la même densité de caractéristiques spectrales, augmentez le nombre de fréquences à 4096.
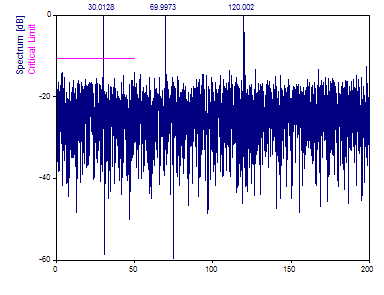
En étendant le spectre à 4x la limite moyenne de Nyquist, toutes les composantes spectrales sont récupérées, y compris le pic à la fréquence 120.
Notez que cet algorithme applique une interpolation interne qui n'est pas sans erreur. Les sinusoïdes des données sont présentes sans bruit, et pourtant un plancher de bruit d'environ -25 dB est observé. Cela limite la mesure dans laquelle cette procédure peut être utilisée pour les analyses Fourier à haute gamme dynamique.
Fenêtre d'observation des données
FlexPro étend l'algorithme pour inclure le fenêtrage. Toutes les fenêtres qui peuvent être créées en utilisant des valeurs temporelles échantillonnées de manière irrégulière sont incluses. Les fenêtres de Tchebychev et Slepian (DPSS) ne sont pas disponibles, bien qu'une fenêtre spéciale d'approximation de Tchebychev soit disponible pour créer le pic spectral le plus net possible pour un niveau de lobe latéral donné.
Changez le type de fenêtre en Cos3 Sidelobe minimum -71dB W=3.
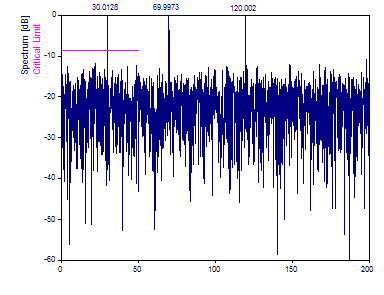
L'erreur intrinsèque de l'algorithme est telle que l'on ne tire que peu d'avantages de la fenêtre d'observation de données.
Limites critiques
Le périodogramme de Lomb-Scargle comprend normalement une limite de confiance traditionnelle basée sur une distribution exponentielle. Cette fonction n'est pas utilisée dans FlexPro. Au lieu de cela, des limites critiques complètes sont disponibles. Comme pour les procédures de Fourier à espacement régulier, des modèles de limite critique distincts sont utilisés pour chacune des fenêtres de données et ils sont basés sur des essais de Monte-Carlo étendus. Comme la distribution des abscisses peut avoir un impact sur la signification, ces limites critiques doivent être considérées comme approximatives.
Atténuation d'amplitude
Changez le type de fenêtre en Rectangulaire -13dB W=1. Définissez la Normalisation à Puissance et définissez le champ Multiple de Nyquist à 3. Sélectionnez Amplitude comme type de spectre.
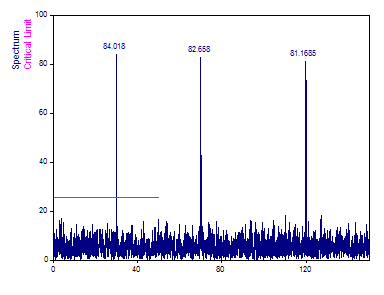
Contrairement à l'analyse de Fourier à espacement régulier, où aucun fenêtrage ne permettait de faire apparaître les amplitudes réelles dans le tracé spectral, une atténuation se produit avec l'algorithme de Lomb-Scargle si l'énergie du signal doit être conservée dans le spectre. L'utilisation d'une fenêtre de données atténue davantage les amplitudes et les énergies.
Le choix de la normalisation permet de compenser l'atténuation.
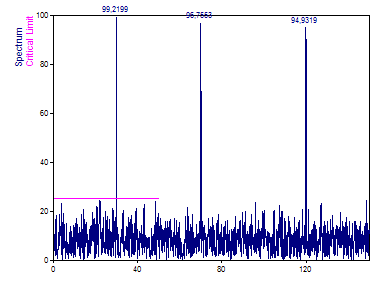
Cliquez sur Suivant. À l'étape 3, cochez les trois options, puis cliquez sur Terminer.
Huit objets au total sont à nouveau créés dans la base de données projet FlexPro. La seule différence est que la phase n'est pas calculée avec l'objet Harmoniques puisqu'elle n'est pas disponible dans cet algorithme.
Références
Une bonne introduction au traitement du signal numérique est :
•Oppenheim, A. V. and Schafer, R. W. (1989). Traitement des signaux en temps discret. Prentice Hall, Englewood Cliffs, NJ.
•H.D. Lüke (1985). "Signalübertragung (Transmission du signal)". Springer-Verlag Berlin, Heidelberg, New York. ISBN 3-540-15526-0.
Les algorithmes FFT utilisés dans FlexPro sont décrits dans :
•C. Temperton, "Implementation of a Self-Sorting In-Place Prime Factor FFT Algorithm", Journal of Computational Physics, v. 58, p. 283, 1985
•R. C. Singleton, "An Algorithm for Computing the Mixed Radix Fast Fourier Transform", IEEE Trans. Audio Electroacoust., v. AU-17, p. 93, June 1969
•L. R. Rabiner, R. W. Schafer, C. M. Rader, "The Chirp z-Transform Algorithm and Its Application", BSTJ, 48, p.1249, May-June 1969
Des informations sur les fenêtres d'observation des données sont données dans :
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, Feb. 1981.
Des informations sur les spectres multitaper peuvent être trouvées dans :
•Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis", Computers and Geosciences, v21, p199, 1995.