Algorithme de Prony
La procédure de Prony est intéressante pour caractériser les sinusoïdes amorties dans un signal.
Pour les données réelles, l'ajustement d'une somme d'exponentielles complexes est équivalent à l'ajustement de sinusoïdes amorties de manière exponentielle. Une sinusoïde amortie de manière exponentielle est un modèle sinusoïdal avec une décroissance du premier ordre ou exponentielle. Les procédures modifiées s'adaptent aux sinusoïdes non amorties en forçant les facteurs d'amortissement à zéro. Plusieurs modifications procédurales ont été mises en œuvre pour améliorer la résistance au bruit de la méthode de Prony.
Les algorithmes de Prony sont des procédures à plusieurs étapes :
1.Effectuer un ajustement AR (autorégressif)
2.Racine des coefficients AR pour les paramètres exponentiels complexes
3.Filtrer racines
4.Ajustement par la méthode des moindres carrés pour les paramètres d'amplitude complexes
5.Créer le modèle final avec le seuillage du signal
Modèle exponentiel complexe
Un modèle de Prony d'ordre m consiste à additionner le produit d'une exponentielle complexe z et d'une amplitude complexe h.
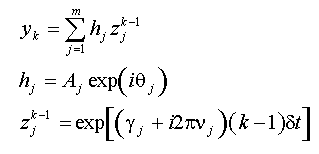
Dans les équations pour h et z, A est l'amplitude de l'exponentielle complexe, g est le facteur d'amortissement, u est la fréquence et q est la phase. FlexPro rapporte les amplitudes complexes et les exponentielles dans la procédure de Prony comme des sinusoïdes réelles amorties :
A est l'amplitude sinusoïdale rapportée, k est le facteur d'amortissement, u est la fréquence, et q est la phase. Notez que le modèle se réduit à une sinusoïde non amortie lorsque l'amortissement (k) est égal à 0 et à une décroissance exponentielle du premier ordre lorsque la fréquence (u) est égale à 0 et la phase (q) à p/2.
Racines polynomiales AR
Un modèle exponentiel complexe se compose d'une amplitude complexe et de paramètres exponentiels. L'estimation des fréquences et des facteurs d'amortissement (les paramètres exponentiels) est effectuée en premier lieu. Ces valeurs sont dérivées des racines complexes d'un ajustement AR (autorégressif). Lorsque le modèle de prévision est utilisé pour le cas amorti, les racines du polynôme AR ajusté sont les paramètres exponentiels complexes du modèle de Prony. Ces racines complexes donnent non seulement les fréquences sinusoïdales, mais aussi les facteurs d'amortissement exponentiels. Un algorithme de prédiction AR est utilisé.
Algorithmes SVD
Les algorithmes SVD mettent en œuvre le seuillage du signal, et en tant que tels, ils sont susceptibles d'offrir des fréquences et des facteurs d'amortissement plus précis pour les composants puisque l'influence du bruit peut être prise en compte.
Comme pour les ajustements AR, l'espace du signal devra être le double du nombre de composantes attendues.
Sélection Racine
Pour stabiliser les procédures de Prony, FlexPro met en œuvre une étape intermédiaire de filtrage des racines. C'est automatique. Les racines de fréquences négatives sont supprimées ainsi que les racines qui apparaissent à la limite de Nyquist. Les algorithmes de Prony amortis peuvent détecter les sinusoïdes, les sinusoïdes amorties et les exponentielles réelles. Si une racine AR est à la fréquence 0, la fonction est une exponentielle réelle. S'il est sur le cercle unitaire, on obtient une sinusoïde non amortie. Dans les autres cas, des sinusoïdes amorties sont détectées. Ceci est strictement une fonction des racines de l'ajustement AR, et ne peut être forcé.
Notez que les exponentielles réelles (désintégrations exponentielles de premier ordre) sont filtrées et n'apparaissent pas dans les modèles de Prony.
Ajustement Moindres Carrés Amplitude Complexe
Une fois les racines identifiées, une régression linéaire des moindres carrés est utilisée pour produire les estimations initiales des paramètres d'amplitude complexes du modèle. Les amplitudes et les phases des sinusoïdes amorties exponentiellement sont ensuite calculées à partir de ces amplitudes complexes.
Seuillage du signal
Comme la méthode de Prony ajuste une série d'exponentielles complexes dans un modèle déterministe, il est possible de tronquer le signal à un nombre spécifié de composantes en éliminant simplement les exponentielles les moins significatives de l'ajustement et de refaire l'ajustement des moindres carrés de l'amplitude complexe avec moins de composantes. Le modèle de Prony final est donc constitué des composants les plus significatifs, déterminés par la valeur fixée comme nombre de composants.
Une fois que les composantes du signal ont été appariées, l'ajustement des moindres carrés de l'amplitude complexe est répété en utilisant uniquement les composantes les plus significatives. Cet ajustement à composante réduite sera plus stable et le spectre d'énergie plus lisse, avec une probabilité moindre de pics spectraux dus au bruit.
Références
Une excellente couverture des algorithmes de Prony peut être trouvée dans :
•S. Lawrence Marple, Jr, "Digital Spectral Analysis with Applications", Prentice-Hall, 1987, p.303-349.