Tutoriel sur l’analyse interspectrale
Ce tutoriel couvre les capacités d'analyse spectrale de FlexPro lorsque deux signaux doivent être comparés pour leur contenu spectral. Les fonctions Interspectre, Interpériodogramme et Cohérence offrent les moyens d'évaluer la similarité et la dissimilarité entre deux signaux. Ces procédures sont souvent utilisées pour des signaux qui proviennent de la même source. Mais il n'est pas nécessaire que ce soit le cas. Deux signaux quelconques ayant la même longueur de données peuvent être évalués.
Ce tutoriel couvre également les fonctions de transfert de Fourier entre un signal d'entrée et un signal de sortie.
Analyse de Fourier
Si vous ne l'avez pas encore fait, il est recommandé de passer par le tutoriel sur l'analyse de Fourier avant de commencer celui-ci. La plupart des principes de l'analyse de Fourier sont couverts dans ce tutoriel. Dans ce tutoriel, nous ne mettrons en évidence que les éléments clés qui se produisent lorsque deux signaux distincts sont évalués à l'aide de méthodes spectrales cross-Fourier.
Deux signaux d'essai
Pour ce tutoriel, nous utiliserons deux signaux de longueur 1024. Le premier sera un signal de référence contenant neuf sinusoïdes de puissance égale, espacées régulièrement sur la plage de Nyquist :
100.0*sin(2π*x*250+p)
100.0*sin(2π*x*500+p)
100.0*sin(2π*x*750+p)
100.0*sin(2π*x*1000+p)
100.0*sin(2π*x*1250+p)
100.0*sin(2π*x*1500+p)
100.0*sin(2π*x*1750+p)
100.0*sin(2π*x*2000+p)
100.0*sin(2π*x*2250+p)
Pour voir l'impact de la variation des amplitudes, des fréquences et des phases dans une analyse trans-spectrale, nous avons modifié les composantes du second signal comme suit :
100.0*sin(2π*x*250+p)
75.0*sin(2π*x*500+p)
50.0*sin(2π*x*750+p)
25.0*sin(2π*x*1000+p)
0.0*sin(2π*x*1250+p)
100.0*sin(2π*x*1502.5+p)
100.0*sin(2π*x*1775+p)
100.0*sin(2π*x*2000+0)
100.0*sin(2π*x*2250+p/2)
Les cinq premières composantes ont une décroissance linéaire de 100% à 0% d'amplitude. Les deux composantes suivantes se décalent vers le haut en fréquence de 0,1% et 1% de la plage de Nyquist. Les deux dernières composantes ont un déphasage de -p et -p/2.
Le taux d'échantillonnage est de 5000 Hz. Ainsi, la fréquence de Nyquist est de 2500 Hz, la fréquence maximale qui peut être détectée. Les valeurs de temps varient de 0 à 0,2046 à un incrément de 0,0002 échantillon. Un bruit gaussien aléatoire de 10% a été ajouté aux deux signaux. Cela produit un plancher de bruit à environ -40 dB par rapport à la plus grande crête.
Sélectionnez la commande Fichier > Ouvrir Base de données projet et ouvrez la base de données projet C:\Users\Public\Documents\Weisang\FlexPro\2021\Exemples\Tutoriels\Analyse spectrale.fpd ou C:>Utilisateurs>Public>Documents Public>Weisang>FlexPro>2021>Exemples\Tutoriels\Analyse spectrale.fpd. Ouvrez le dossier Tutoriels et son sous-dossier Analyse spectrale croisée, puis double-cliquez pour ouvrir le graphique 2D appelé Données.
Voici un graphique des deux signaux. Il y a 1024 valeurs à virgule flottante.
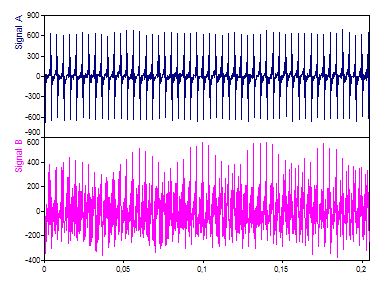
Tout ce que l'on peut déduire du domaine temporel, c'est qu'il existe d'importantes similitudes et d'importantes différences.
Spectres de Fourier
Fermez le graphique et mettez en surbrillance l'ensemble de données Signal A, le signal de référence.
Cliquez sur Insérer[Analyses] > Assistant d'analyse.
Sélectionnez la catégorie Analyses spectrales, puis Analyses de Fourier. Ensuite, sélectionnez Spectre de Fourier. Notez que le résultat de certaines procédures spectrales dépend de l'ordre des ensembles de données sélectionnés. Vous devez donc toujours vérifier soigneusement que l'ordre affiché dans la liste intitulée"3.) Affecter des ensembles de données :" est correct. Si l'ordre n'est pas correct, sélectionnez l'entrée et déplacez-la vers le haut ou vers le bas en cliquant sur les boutons fléchés situés au-dessus de la liste. Dans notre exemple, le signal A devrait être la première entrée. Cliquez sur Suivant.
Sélectionnez Amplitude comme type de spectre. Pour le type de fenêtre, sélectionnez Cos3 Sidelobe minimum -71dB W=3. Assurez-vous que la longueur de la FFT est définie sur longueur des données ou sur 1024. Sélectionnez Nombre maximal de pics sous Options et entrez la valeur 9. Ensuite, définissez la limite critique du bruit blanc % sur Aucun. Si aucune étiquette n'est visible au-dessus des pics, cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes d'amplitude apparaissent.
Le tracé de Fourier dans l'assistant d'analyse devrait être le suivant :
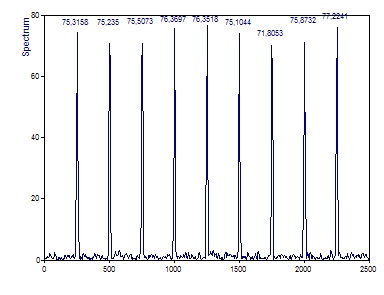
Comme il est typique, les pics ne sont pas centrés dans les canaux de Fourier, et le déplacement de l'harmonique par rapport au centre du canal n'est pas constant. Lorsque le déplacement est le plus faible, les amplitudes sont les plus élevées. Notez également que le fenêtrage entraîne la propagation d'une partie de l'information spectrale aux canaux adjacents. C'est pourquoi les amplitudes dans les canaux de crête ne représentent qu'environ 75% des amplitudes réelles des harmoniques.
Cliquez sur Annuler et répétez les mêmes étapes pour l'ensemble de données Signal B.
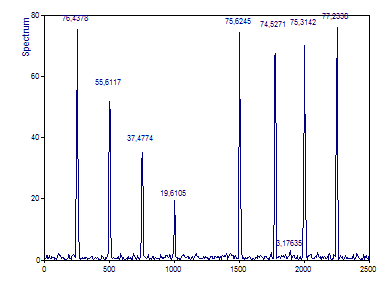
La seule différence apparente dans le second spectre est la diminution de l'amplitude des composantes spectrales initiales. Un peu plus subtil est le changement de fréquence des sixième et septième composants.
Interspectre de Fourier
Cliquez sur Annuler pour fermer l'assistant. Sélectionnez les deux ensembles de données Signal A et Signal B en appuyant sur la touche CTRL pendant la sélection.
Cliquez sur Insérer[Analyses] > Assistant d'analyse.
Sélectionnez la catégorie Analyses spectrales, puis Procédures spectrales à deux signaux. Ensuite, sélectionnez Interspectre de Fourier. Cliquez sur Suivant.
Comme pour les analyses de Fourier individuelles, pour le Type de Spectre, sélectionnez l'option Amplitude. Pour le type de fenêtre, sélectionnez la valeur Cos 3 Minimum Sidelobe -71dB W=3. Assurez-vous que la longueur de la FFT est définie sur longueur des données ou sur 1024. Sélectionnez Nombre maximal de pics sous Options et entrez la valeur 9. Si aucune étiquette n'est visible au-dessus des pics, cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes d'amplitude apparaissent.
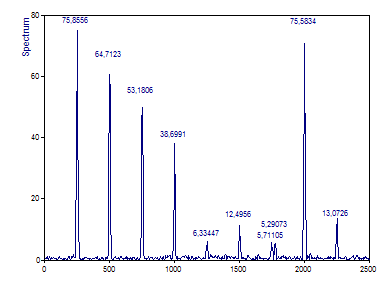
Lorsque seules les amplitudes varient, comme c'est le cas pour les deuxième à quatrième composantes, les amplitudes interspectrales se situent entre les deux spectres.
En cinquième position, il y a une harmonique dans un signal et absolument rien dans l'autre. Et pourtant, il y a toujours un petit pic. Il s'agit du interspectre entre la composante du signal de forte puissance dans la référence et le bruit dans le second signal à cette fréquence particulière. Notez que la présence d'un pic à une fréquence donnée ne permet pas de déduire qu'il existe un contenu harmonique significatif dans les deux signaux. Dans ce cas, il y a un contenu harmonique significatif dans seulement le premier des signaux.
Dans la sixième position, nous voyons ce qui se passe lorsque deux pics sont décalés de seulement 0,1% de la plage de Nyquist. Il y a toujours une petite caractéristique trans-spectrale, mais elle est mineure. Nous sommes face à un décalage de seulement 2,5 Hz dans un spectre qui couvre 2500 Hz.
Dans la septième position, le décalage de fréquence est de 1% de Nyquist, 25 Hz dans cet exemple. Il y a maintenant deux caractéristiques interspectrales, l'une à la fréquence centrale de la composante dans le premier signal, et l'autre à la fréquence centrale de la composante dans le second. Ce sont des pics de bruit dans le sens où il n'y a pas de contenu de signal interspectral.
Si la phase est déphasée de π, comme dans la huitième composante, il s'agit de la même différence que la modélisation avec les sinus et les cosinus. La totalité de l'amplitude est récupérée. Toutefois, si le déphasage est, dans le pire des cas, celui de π/2, comme dans la neuvième composante, une grande partie de l'amplitude interspectrale est perdue.
Interpériodogramme
Tout comme le Périodogramme fait la moyenne des segments individuels qui se chevauchent pour produire une estimation de Fourier à variance réduite au détriment de la résolution en fréquence, ces mêmes principes sont applicables aux périodogrammes croisés.
Sélectionnez l'algorithme Interpériodogramme. Assurez-vous que l'Amplitude est sélectionnée et que le Type de fenêtre est réglé sur Cos 3 Sidelobe minimum -71dB W=3. La longueur du segment est la longueur des données/4 ou 256 et la longueur de la FFT est fixée à la longueur du segment ou 256. Le chevauchement doit être de 50%. Sélectionnez Nombre maximal de pics sous Options et entrez la valeur 9. Si aucune étiquette n'est visible au-dessus des pics, cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes d'amplitude apparaissent.
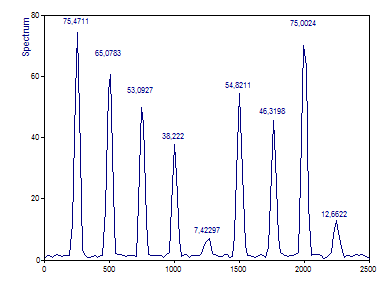
Les pics sont beaucoup plus larges car la résolution de Fourier n'est que d'un quart de l'interspectre d'un seul segment. Cette résolution de fréquence réduite est un facteur important dans cet exemple.
La réduction de la variance est visible dans le spectre beaucoup plus lisse. Les amplitudes interspectrales dans les composantes initiales sont déterminées avec plus de précision. Le interspectre entre l'harmonique et le bruit dans la cinquième position de fréquence est maintenant un pic lisse de faible puissance.
La plus grande différence reste avec les sixième et septième composantes. En raison de la résolution de fréquence réduite, il y a maintenant un chevauchement important entre les composants. Le décalage de 2,5 Hz se traduit par une amplitude interspectrale qui est réduite de moins d'un tiers. Même le décalage de 25 Hz entraîne une réduction de l'amplitude interspectrale qui est inférieure à la moitié de ce qui serait le cas si les fréquences correspondaient entièrement.
Nous allons maintenant prendre des mesures pour améliorer la résolution de l'Interpériodogramme . Puisque nous n'effectuons pas d'analyse de Fourier croisée à haute dynamique (recherche de composants de très faible puissance qui sont communs), nous utiliserons une fenêtre qui n'entraîne pas autant de perte de résolution dans le domaine des fréquences. Nous allons également doubler la résolution en utilisant un segment qui a la moitié de la longueur des données. Pour améliorer la variance, ou au moins pour produire un spectre plus lisse, nous allons faire la moyenne de plus de segments en augmentant le chevauchement.
Définissez le type de fenêtre sur Cos2 Hanning -31dB W=2, la longueur du segment sur 512, la longueur de la FFT sur la longueur du segment ou 512. Modifiez le chevauchement à 90%.
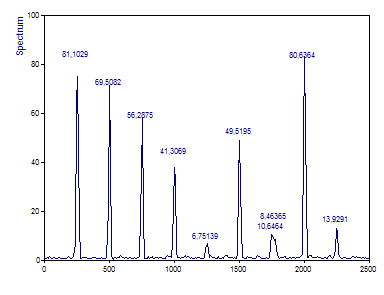
Notez que les pics sont beaucoup plus nets et que les pics interspectraux sont beaucoup moins importants pour les sixième et septième composantes qui diffèrent en fréquence. Une partie de la régularité a été perdue, mais les amplitudes sont maintenant un peu plus élevées en raison de moins de débordement dans les bacs adjacents.
Cohérence
Lorsque plusieurs segments sont utilisés, il est possible de produire un spectre de Cohérence. La cohérence est égale à 1 lorsqu'il y a similitude du contenu spectral à une fréquence donnée et à 0 lorsque les signaux sont dissemblables ou totalement non corrélés. Il s'agit souvent d'un moyen pratique de rechercher des zones dans un spectre où un signal renvoyé est incohérent, c'est-à-dire qu'il présente des différences de fréquences harmoniques.
Sélectionnez la procédure de Cohérence et le type spectral Cohérence. Laissez intacts tous les paramètres de la section Cross-Periodogram. Cliquez sur Basculer les étiquettes pour désactiver les étiquettes de crête.
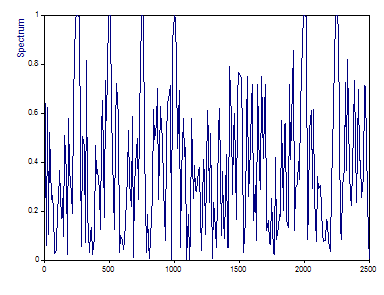
Bien que les composantes initiales des deux signaux diffèrent en amplitude, cela n'entre pas en ligne de compte dans la MSC, la cohérence magnitude-carré. Il est démontré que les quatre premières composantes ont une cohérence qui atteint 1.
La cinquième composante, présente dans un signal et absente dans l'autre, ne montre rien au-dessus de la ligne de base.
Les sixièmes composantes, qui ne diffèrent que de 2,5 Hz en fréquence entre les deux signaux, ont une cohérence plus élevée que les septièmes composantes, qui diffèrent entièrement de 25 Hz en fréquence. Notez également que cette septième composante produit une cohérence constamment faible.
Le MSC est également indépendant de la phase. Les huitième et neuvième composantes produisent une cohérence de 1, malgré les déphasages.
Spectre du rapport signal/bruit
Si plusieurs segments sont utilisés, il est possible de produire un spectre de rapport signal/bruit. Cette méthode utilise les valeurs de cohérence pour produire des estimations du rapport signal/bruit à chaque fréquence du spectre.
Pour le type de spectre, sélectionnez Rapport signal/bruit dB.
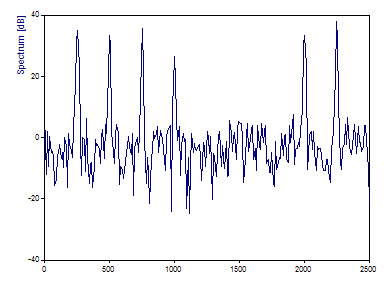
Nous savions que nous avions généré un plancher de bruit à environ -40 dB sur les deux signaux. Ici, nous voyons des pics qui s'élèvent à environ 40 dB au-dessus du plancher de bruit. Comme pour la cohérence, les composantes dont l'amplitude et la phase varient présentent un rapport S/N complet ou proche du complet. Les composantes décalées de 2,5 Hz en fréquence présentent une légère amélioration du rapport S/N, mais les composantes décalées de 25 Hz semblent impossibles à distinguer du bruit. Les composantes décalées de 25 Hz, cependant, semblent indiscernables du bruit.
Fonction de transfert
La fonction de transfert de Fourier est une carte du domaine des fréquences qui représente les propriétés de transfert d'un système. Dans notre exemple, le second signal contenait toujours la même énergie ou une énergie moindre à chacune des fréquences, à l'exception des deux cas où il y avait des décalages de fréquence.
Contrairement aux spectres de cohérence et de SNR, une fonction de transfert peut être calculée avec un seul segment. Nous utiliserons donc les paramètres que nous avions initialement appliqués à la procédure Cross-Spectral.
Sélectionnez la fonction de transfert et le type de spectre dB. Sélectionnez pour le type de fenêtre Cos 3 Sidelobe minimum -71dB W=3. Définissez la longueur de la FFT à longueur de l'ensemble de données ou à 1024. Cliquez sur Basculer les étiquettes pour désactiver les étiquettes de crête. Cliquez sur le graphique supérieur, puis sur le symbole Activer le curseur (le premier dans la boîte à outils sous les graphiques).
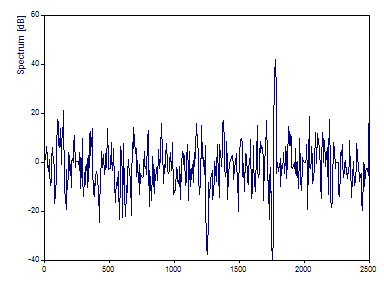
Placez le curseur sur 250 Hz, qui est la position de la première composante. La valeur est d'environ 0,17 à 0,18 dB. Si vous placez le curseur sur 500, 750 et 1000, vous devriez voir -2,5 à -2,6 dB, -6,0 dB et -11,7 dB.
Elles correspondent aux réductions d'amplitude de 1/4, 1/2 et 3/4 de ces harmoniques dans le second signal.
Notez qu'il y a une profonde vallée dans la fonction de transfert à 1250 Hz, où le pic du second signal est complètement absent.
Il y a également une vallée profonde dans la fonction de transfert à 1750 Hz, où là encore il n'y a pas de pic dans le signal renvoyé, et un pic aigu dans la fonction de transfert à 1775 Hz, où il y a un pic aigu dans le signal renvoyé, mais rien dans le signal d'entrée.
Application d'une fonction de transfert aux données d'entrée
Notez que pour les applications réelles, il n'est pas très utile de calculer une fonction de transfert à partir de signaux du type de ceux utilisés dans la section ci-dessus. Nous pouvons facilement voir que le signal B n'est pas la réponse d'un système LTI car les fréquences ont été décalées, alors que les systèmes LTI ne changent que les phases et les amplitudes des composantes spectrales présentes. En outre, pour obtenir une image complète d'un système LTI et donc une fonction de transfert bien définie, le signal d'entrée doit stimuler tous les modes du système LTI. Un tel signal d'entrée serait par exemple un bruit blanc.
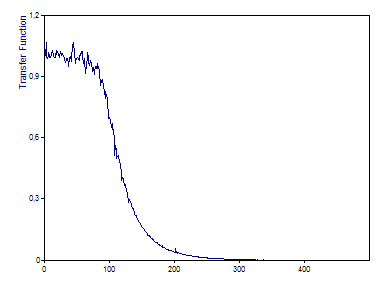
Pour le démontrer, la base de données projet d'exemple contient un ensemble de données supplémentaire appelé Bruit d'entrée et un objet appelé Bruit de sortie, qui est une version filtrée passe-bas des données de bruit d'entrée. L'objet Fonction de transfert a déjà été configuré pour calculer la fonction de transfert des signaux reflétant ce filtre passe-bas. Le graphique du même nom permet de le visualiser. Le filtre passe-bas utilisé est un filtre Butterworth d'ordre 4 avec une fréquence de coupure de 100 Hz.
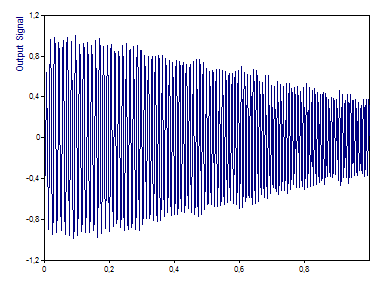
Comme dernier exercice, nous allons appliquer la fonction de transfert à un signal d'entrée afin de générer une estimation du signal de sortie. Sélectionnez l'objet Signal d'entrée, qui est une sinusoïde chirp dont la fréquence est comprise entre 75 Hz et 125 Hz. Cliquez avec le bouton droit de la souris, pointez sur Insérer un objet, puis cliquez sur Formule. Entrez la formule suivante : IRFFTn(FFTn('Input Signal') * 'Transfer Function')... Cliquez maintenant sur Exécuter pour tester la formule. Vous devriez recevoir un signal avec 1000 points. Cliquez sur OK et fermez la fenêtre de la formule. Mettez à nouveau en surbrillance le nom de la formule et cliquez sur la touche F2 ). Saisissez maintenant le nouveau nom Signal de sortie. La formule calcule le spectre de notre signal d'entrée et le multiplie par la fonction de transfert. Ce calcul simple du signal de sortie est possible car une convolution dans le domaine temporel est égale à une multiplication dans le domaine fréquentiel. Lorsque vous multipliez les spectres, vous devez veiller à ce que le nombre de fréquences et l'espacement des fréquences soient les mêmes pour les deux spectres. Pour que ce tutoriel reste aussi simple que possible, nous avons généré notre fonction de transfert à partir d'un segment unique égal à la longueur des données du signal de bruit d'entrée et du signal chirp d'entrée. Si nous avions fait la moyenne des segments qui se chevauchent, notre fonction de transfert aurait été à la fois plus lisse et plus courte.
Nous avons généré un ensemble de données avec 1000 valeurs réelles dont l'amplitude diminue lorsque la fréquence augmente. La fréquence de coupure de 100 Hz est atteinte exactement au milieu de notre signal d'entrée chirp. Là, comme prévu, l'amplitude du signal renvoyé est amortie d'environ -3 dB.
Références
•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.