Tutoriel sur l’analyse spectrale temps-fréquence
Ce tutoriel couvre les capacités d'analyse spectrale de FlexPro pour les données non-stationnaires. Il couvre à la fois la Transformée de Fourier à court terme (STFT) et la Transformée en ondelettes continue (CWT). Ces procédures sont utiles pour étudier les propriétés changeantes au sein d'un flux de données ainsi que pour identifier les régions stationnaires pour les analyses conventionnelles de Fourier et paramétriques.
Un signal d'essai contenant quatre sinusoïdes séquentielles
Pour ce tutoriel, nous allons utiliser un ensemble de données non stationnaires avec quatre régions de données contenant chacune une sinusoïde de fréquence différente.
Sélectionnez la commande Fichier > Ouvrir Base de données projet et ouvrez la base de données projet C:\Users\Public\Documents\Weisang\FlexPro\2021\Exemples\Tutoriels\Analyse spectrale.fpd ou C:>Utilisateurs>Public>Documents Public>Weisang>FlexPro>2021>Exemples>Tutoriels>Analyse spectrale.fpd. Ouvrez le dossier Tutoriels et son sous-dossier Analyse temps-fréquence, puis double-cliquez pour ouvrir le graphique 2D appelé Données.
C'est un graphique du signal. Il y a 1024 valeurs à virgule flottante.
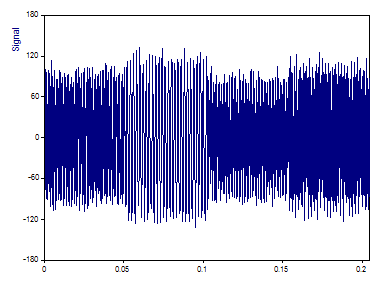
Les valeurs X (temps) varient de 0 à 0,2047 avec un incrément de 0,0002 échantillon. La fréquence de Nyquist est donc de 2500 (la moitié de la fréquence d'échantillonnage de 5000). Les quatre sinusoïdes ont été générées avec les amplitudes, les fréquences et les phases suivantes :
100.0*sin(2π*x*1000)+
120.0*sin(2π*x*500+p/2)+
90.0*sin(2π*x*2000+p)+
110.0*sin(2π*x*1500+3p/2)
Un bruit gaussien (blanc) aléatoire de 10 % a été ajouté pour un plancher de bruit de -20 dB.
La perte d'information temporelle dans une transformée de Fourier
Nous allons commencer par explorer un spectre de Fourier de base de cet ensemble de données.
Fermez le graphique et mettez en évidence l'ensemble de données Signal.
Cliquez sur Insérer[Analyses] > Assistant d'analyse.
Sélectionnez la catégorie Analyse de Fourier sous Analyse spectrale. Ensuite, sélectionnez Spectre de Fourier. Cliquez sur Suivant.
Pour le type de spectre, sélectionnez Amplitude. Pour le type de fenêtre, sélectionnez Rectangulaire -13dB W=1. Assurez-vous que la longueur FFT est réglée sur Longueur FFT sur la longueur de l'ensemble de données ou 1024. Sélectionnez l'option Nombre maximal de pics et entrez la valeur 4. Ensuite, définissez la limite critique du bruit blanc % sur Aucun. Si aucune étiquette n'est visible au-dessus des pics, cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes d'amplitude apparaissent.
Le tracé de Fourier dans l'assistant d'analyse devrait être le suivant :
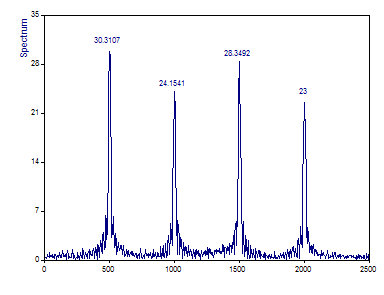
Bien que le spectre de Fourier identifie correctement les fréquences des quatre composantes séquentielles, il n'y a aucune indication de l'endroit où ces harmoniques commencent et finissent dans le temps. Toute information de localisation temporelle est perdue puisque chaque composant est supposé être d'une durée infinie.
De plus, comme chaque composante n'est présente que pendant environ un quart de la longueur totale des données, chaque amplitude représente environ un quart de sa valeur dans l'harmonique transitoire.
Un signal doit être stationnaire au sens large pour qu'un spectre de Fourier soit précis. Cela signifie que le contenu spectral doit être constant en termes de fréquences et de puissances pendant toute la durée de l'échantillonnage. Les analyses CWT et STFT sont toutes deux efficaces pour analyser les signaux non stationnaires car elles fournissent un spectre temps-fréquence des données.
Spectre de la transformée de Fourier à court terme
La transformée de Fourier à court terme (STFT) est similaire au périodogramme ou à la FFT à recouvrement segmenté, sauf qu'une valeur temporelle centrale est attribuée à chaque segment. À moins qu'il ne soit nécessaire de récupérer directement l'amplitude ou la puissance des pics spectraux, une fenêtre d'onservation des données est généralement utilisée pour créer la meilleure localisation temporelle possible.
Les spectres temps-fréquence sont intrinsèquement flous. Plus la résolution temporelle est bonne, moins la résolution fréquentielle est bonne. Le STFT est le meilleur moyen de se faire une idée de cet effet.
Cliquez sur Retour pour revenir à l'étape 1 de l'assistant d'analyse. Sélectionnez le Spectre Temps-Fréquence et de là STFT. Cliquez sur Suivant pour passer à l'étape 2. La procédure de transformation de Fourier à court terme (STFT ) est automatiquement sélectionnée.
Pour le Type de spectre, sélectionnez dB normalisé. Définissez le type de fenêtre sur Cos2 Hanning -31dB W=2. Les valeurs par défaut sont sélectionnées pour le point de départ. Assurez-vous que la longueur de la FFT est réglée sur Segment Length et que la longueur du segment est de 256, ce qui est égal à 1/4 de la longueur des données. Définissez le % de chevauchement à 50.
Pour placer le temps le long de l'axe X, comme c'est généralement le cas avec les spectres Temps-Fréquence, cochez Fréquence est Z. Définissez la plage de dB maximum à 20 et gardez les fréquences STFT maximum à un nombre illimité.
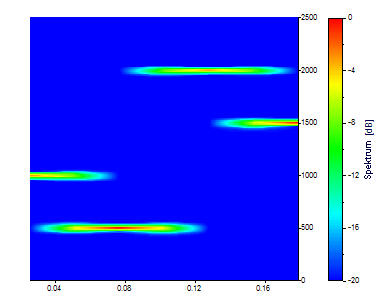
Ces paramètres produisent 7 instantanés temporels, chacun d'une longueur de 0,05 seconde. Il existe 129 fréquences. Alors qu'il y a une définition nette des composantes aux fréquences de 500, 1000, 1500 et 2000, la nature séquentielle des quatre harmoniques est obscurcie par la très mauvaise définition dans le temps. De plus, comme le temps attribué à un instantané est le temps moyen dans le segment, il y a une zone appréciable aux deux bornes temporelles où aucune information spectrale n'est disponible.
Une façon très simple d'augmenter la densité dans le temps est d'augmenter le % de chevauchement.
Modifiez le % de chevauchement à 90.
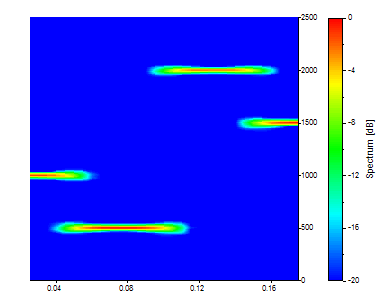
Il y a maintenant 31 instantanés temporels différents qui composent ce spectre. Les mêmes 129 fréquences sont présentes. Bien que cela produise une amélioration modeste de la résolution temporelle, chaque instantané est toujours une moyenne sur un quart des données. Pour améliorer la résolution temporelle, il est nécessaire de diminuer la longueur des segments.
Pour diviser par deux la longueur du segment, changez-la en 128. Conserver le % de chevauchement à 90.
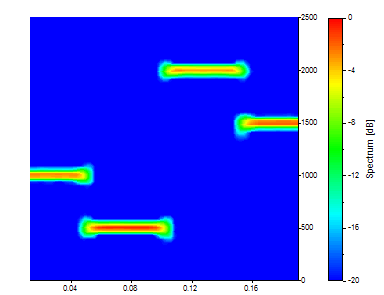
Il y a maintenant 75 segments temporels, chacun représentant une moyenne d'un huitième des données. Il existe 65 fréquences. Le compromis temps-fréquence devrait maintenant être apparent. Il y a maintenant une définition beaucoup plus forte dans le temps, mais la résolution en fréquence s'est considérablement dégradée.
Modifiez la longueur du segment à 64. Conserver le % de chevauchement à 90.
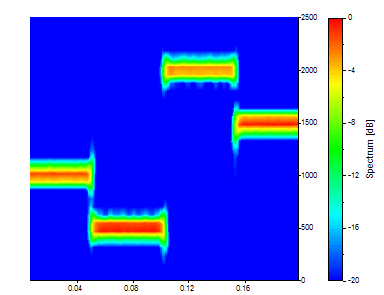
Il y a maintenant 161 segments temporels, chacun représentant une moyenne sur 1/16e des données. Il existe 33 fréquences. La définition dans le temps est encore améliorée, mais la résolution en fréquence est devenue nettement plus floue. Allez une étape plus loin. Modifiez la longueur du segment à 32. Conserver le % de chevauchement à 90.
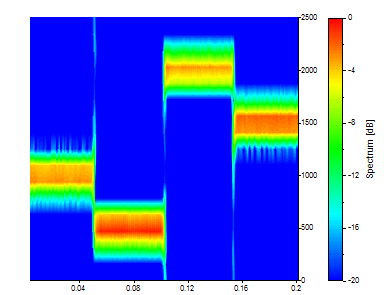
Il y a maintenant 331 valeurs temporelles mais seulement 17 nœuds de fréquence dans la grille spectrale. Les instantanés temporels représentent des moyennes sur 1/32e des données et la définition dans le temps est donc assez nette. D'autre part, les pics se rejoignent presque dans le domaine des fréquences.
La visualisation est parfois plus claire avec un véritable tracé de surface en 3D.
Cliquez sur Vue standard. Pour améliorer la grille de rendu 3D, modifiez la longueur de la FFT à 128.
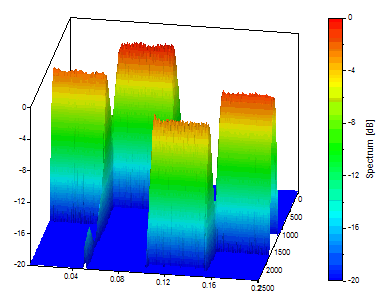
C'est un bon moyen de visualiser un compromis temps-fréquence qui favorise la résolution dans le temps. Nous allons maintenant revenir aux paramètres initiaux qui favorisaient la fréquence.
Définissez la longueur du segment à 256. Définissez la longueur de la FFT à Longueur de segment et le % de chevauchement à 90.
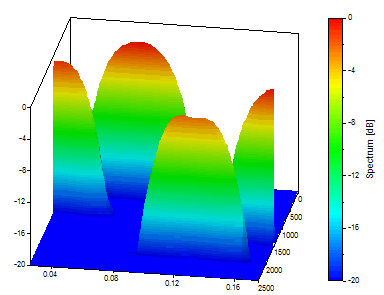
Il s'agit d'une bonne visualisation d'un compromis temps-fréquence qui favorise la résolution en fréquence au détriment d'un flou important dans le temps.
L'optimisation des paramètres de la STFT peut s'avérer difficile. La STFT est une technique à résolution unique. Le même compromis temps-fréquence est présent partout dans le spectre, quelle que soit la fréquence. Bien que la STFT nécessite un réglage précis, un spectre peut facilement donner des amplitudes et des puissances spectrales directement à partir de la hauteur des pics spectraux. Utilisez une fenêtre d'observation et réglez la normalisation sur Amplitude ou utilisez une fenêtre rectangulaire combinée à un chevauchement élevé.
Vous obtiendrez le graphique suivant si vous réglez le type de spectre sur Amplitude, le type de fenêtre sur Rectangulaire -13dB W=1 (pas de fenêtrage), la longueur du segment sur 64, la longueur de la FFT sur 256 et le % de chevauchement sur 90.
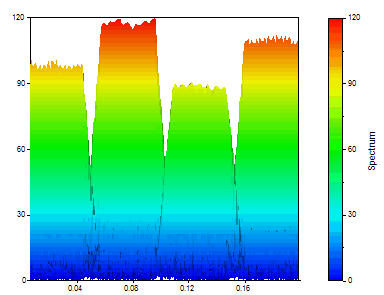
Spectres Transformée en Ondelettes Continues
La STFT utilise des fonctions de base sinusoïdales en phase. La durée infinie des fonctions sinus nécessite la transformation de segments fenêtrés du flux de données. Si les fonctions de base étaient elles-mêmes de durée finie, un spectre pourrait être créé à partir de la corrélation entre les versions décalées et étirées/compressées de cette "ondelette" mère de durée limitée et le flux de données.
C'est l'essence même de la Transformation en ondelettes continues (CWT).
Malgré l'éventail impressionnant de formes d'ondelettes, l'utilisation des ondelettes pour l'analyse spectrale temps-fréquence est généralement plus facile que l'optimisation de la STFT. Et dans la plupart des cas, les différences entre les diverses ondelettes mères et les paramètres n'ont pas un grand impact sur le spectre temps-fréquence résultant. La sélection de l'ondelette mère et du paramètre ajustable implique généralement la sélection d'un compromis temps-fréquence.
Sélectionnez Transformation en ondelettes continues (CWT) et dB normalisé comme Type de spectre. Définissez le type d'ondelette sur Morlet et l'ajustement (nombre d'ondes) sur 8. Définissez le tampon zéro à 1024 (tamponnez les 1024 données à 2048, la prochaine puissance de 2), le nombre de fréquences à 40 et gardez la fréquence de début à 0 et la fréquence de fin à 2500 (la gamme complète de Nyquist). Assurez-vous que la case Frequency is Z est cochée, que la plage maximale de dB est fixée à 20 et que les valeurs maximales de temps CWT sont fixées à 1024 (pour tenir compte de la longueur de données de 1024).
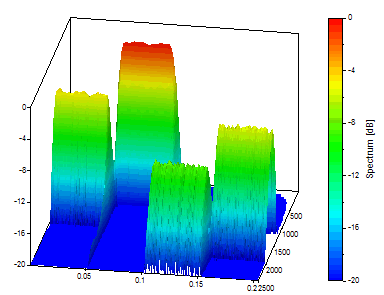
C'est un bon spectre temps-fréquence CWT. En fait, on obtient des résultats respectables, quelle que soit l'ondelette mère ou la valeur de son paramètre réglable. Vous pourriez probablement utiliser l'ondelette de Morlet avec un nombre d'onde de 8 pour tous les travaux d'analyse temps-fréquence, et ne jamais manquer les raffinements qui découleraient de la sélection de l'ondelette dont la forme est la plus compatible avec les oscillations des données et dont le nombre d'oscillations donne la résolution temps-fréquence optimale.
Pour s'en convaincre, nous allons explorer les extrêmes offerts par FlexPro.
Pour évaluer le compromis temps-fréquence dans l'analyse par ondelettes, nous allons rétablir un tracé de contour. Cliquez sur Vue plan.
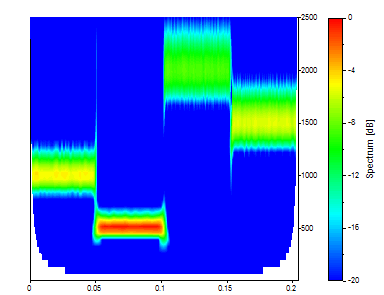
Changez l'ajustement pour le nombre d'onde 20.
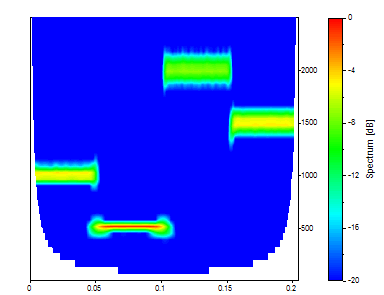
Le Morlet avec un paramètre ajustable (nombre d'onde) de 20 produit une meilleure localisation de la fréquence et une moins bonne localisation du temps.
Changez l'ajustement à 50.
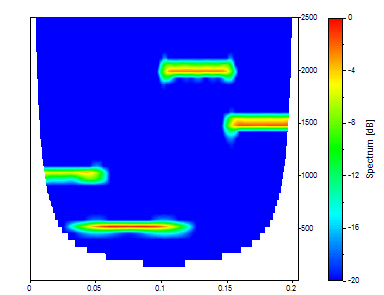
Le Morlet avec un paramètre ajustable (nombre d'onde) de 50 produit une définition nette de la fréquence mais une mauvaise localisation dans le temps.
Définissez le type d'ondelette sur la dérivée gaussienne et l'ajustement sur 2.
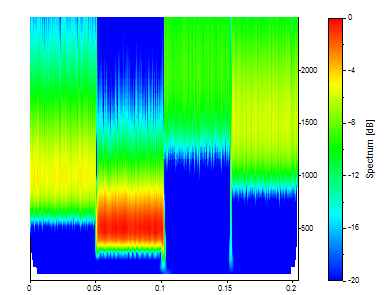
L'ondelette dérivée gaussienne avec un paramètre ajustable de 2 produit la localisation temporelle la plus nette mais, comme on peut le constater, une localisation fréquentielle très floue.
Analyse multirésolution
La CWT est une technique de multi résolution temps-fréquence. Si vous inspectez les graphiques précédents, vous remarquerez que le pic de fréquence le plus bas a la magnitude spectrale CWT la plus élevée et est le moins étalé en fréquence des quatre composantes du signal. Le pic de fréquence le plus élevé présente systématiquement la magnitude spectrale la plus faible et est le plus étalé en fréquence des quatre composantes.
Cette propriété est un sous-produit de l'algorithme CWT plutôt qu'une considération de conception. L'analyse multirésolution présente des avantages et des inconvénients. Si les composantes de haute fréquence sont intermittentes avec une durée très courte, la position optimale serait d'arbitrer la résolution de fréquence afin de capturer avec précision son apparition et sa disparition dans le temps. Si les composantes de basse fréquence sont de longue durée, l'état optimal serait d'échanger la résolution temporelle contre une estimation plus précise de la fréquence. Lorsque ces conditions sont réunies, l'analyse multirésolution du CWT est un atout.
Si la persistance est indépendante de la fréquence, ou si l'objectif principal est de récupérer les amplitudes et la puissance directement à partir des magnitudes spectrales, la propriété multirésolution de la CWT est un inconvénient.
Redondance de fréquence CWT
Contrairement à la transformée en ondelettes discrètes (DWT) traditionnellement utilisée pour l'analyse des ondelettes, la CWT peut être évaluée à n'importe quel ensemble de fréquences souhaité. Ces fréquences peuvent se chevaucher avec une mesure arbitraire de redondance et elles peuvent être espacées linéairement, logarithmiquement ou dans n'importe quelle séquence. Étant donné qu'une FFT distincte doit être enregistrée pour chaque fréquence évaluée, FlexPro limite le nombre total de fréquences à 500. C'est cette redondance de fréquences qui permet à la CWT d'offrir une résolution bien plus élevée que la DWT.
Sélectionnez à nouveau l'ondelette Morlet. Définissez un nombre d'onde de 12. Spécifiez 100 comme nombre de fréquences, 400 comme fréquence de départ et 1200 comme fréquence finale.
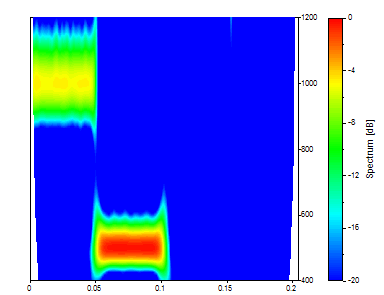
Toute la puissance analytique de l'analyse spectrale CWT est maintenant concentrée dans la bande de fréquence 400 à 1200.
Zéro padding de la FFT et effets de bord
Contrairement à une analyse de Fourier classique où le spectre est généré par la transformée, la FFT est utilisée dans la CWT uniquement pour effectuer une convolution rapide de l'ondelette mise à l'échelle et traduite avec le flux de données. Dans le CWT, les fonctions de base sont des ondelettes mises à l'échelle et décalées, et non les sinus et cosinus de Fourier. Le rajout de zéro (zero padding) n'a qu'un seul but dans le CWT, celui d'éviter les effets d'enveloppement (aliasing) dans la procédure de convolution rapide. L'emballement est totalement évité à toutes les fréquences lorsque la longueur de la FFT est égale à deux fois la longueur du flux de données. Il est souvent possible d'effectuer un rajout de zéro (zero padding) à la puissance deux suivante et d'éviter tout wraparound perceptible, tout en obtenant les convolutions les plus rapides possibles.
Lorsqu'une FFT à N exact est utilisée pour la convolution rapide, l'enveloppement aux basses fréquences est facilement apparent. Cet effet d'enveloppement diminue avec la fréquence. Cela explique l'absence d'un effet d'enveloppement avec la composante de fréquence la plus élevée. Si le contenu en basse fréquence est négligeable, ou si les données sont cycliques dans la bande traitée, il n'est pas nécessaire d'utiliser le rajout de zéro (zero padding).
Lorsque le rajout de zéro (zero padding) est utilisé pour éviter cet effet, la puissance associée à l'enroulement est rejetée. Cela se traduit par une diminution de la puissance près des bords de l'enregistrement des données. Dans la terminologie CWT, cette zone où la puissance peut être diminuée est appelée le cône d'influence. Le cône d'influence est particulièrement important lorsque l'espacement des fréquences est logarithmique.
Définissez le nombre d'ondes du Morlet sur 100, le tampon zéro sur 0, le nombre de fréquences sur 40, la fréquence de début sur 0 et la fréquence de fin sur 2500.
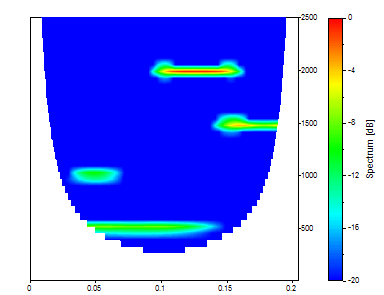
Dans ce cas, le nombre d'onde très élevé entraîne un cône d'influence beaucoup plus grand. La composante de fréquence la plus basse s'enroule en fait à droite de l'échelle de temps. Ceci n'apparaît pas dans FlexPro car les informations situées dans ce cône d'influence ne sont pas tracées.
Définissez le nombre d'onde de Morlet à 12, puis cliquez sur Suivant. Cochez les deux options de l'étape 3 et cliquez sur Terminer.
Quatre objets au total sont créés dans la base de données projet FlexPro.
"Spectre" est l'objet d'analyse. Il s'agit de l'objet qui effectue l'analyse spectrale. L'objet d'analyse peut être ouvert en double-cliquant dessus.
"Spectre" est le tracé du spectre temps-fréquence généré par l'assistant d'analyse. Il utilise l'objet Spectre :
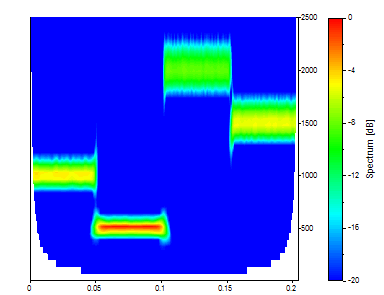
"Donnée2" est un tracé des données originales du domaine temporel.
"Temps-Fréquence" est un document qui contient les tracés spectraux et les données.
Références
Une bonne introduction au traitement du signal numérique est :
•Oppenheim, A. V. and Schafer, R. W. (1989). Traitement des signaux en temps discret. Prentice Hall, Englewood Cliffs, NJ.
•H.D. Lüke (1985). "Signalübertragung (Transmission du signal)". Springer-Verlag Berlin, Heidelberg, New York. ISBN 3-540-15526-0.
Les algorithmes FFT utilisés dans FlexPro sont décrits dans :
•C. Temperton, "Implementation of a Self-Sorting In-Place Prime Factor FFT Algorithm", Journal of Computational Physics, v. 58, p. 283, 1985
•R. C. Singleton, "An Algorithm for Computing the Mixed Radix Fast Fourier Transform", IEEE Trans. Audio Electroacoust., v. AU-17, p. 93, June 1969
•L. R. Rabiner, R. W. Schafer, C. M. Rader, "The Chirp z-Transform Algorithm and Its Application", BSTJ, 48, p.1249, May-June 1969
Des informations sur les fenêtres d'observation des données sont données dans :
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, Feb. 1981.
Pour ceux qui souhaitent comprendre les subtilités de l'application de l'analyse par ondelettes à des données du monde réel, il existe un article bien écrit qui couvre le CWT de manière approfondie et accessible :
•Christopher Torrence and Gilbert Compo, "A Practical Guide to Wavelet Analysis", Bulletin of the American Meteorological Society, v.79, no.1, p.61-78. January 1998
Cette référence explique le CWT dans le contexte de l'analyse des données des séries chronologiques d'El Nino. Les auteurs ont également publié un paquetage FORTRAN d'analyse des ondelettes CWT du domaine public, WAVEPACK. Le document et le code WAVEPACK sont disponibles à l'adresse suivante : http://paos.colorado.edu/research/wavelets/.