Transformée en ondelettes continues (CWT)
La transformation en ondelettes continues (CWT) est utilisée pour décomposer un signal en ondelettes. Les ondelettes sont de petites oscillations très localisées dans le temps. Alors que la Transformée de Fourier décompose un signal en sinus et cosinus de longueur infinie, perdant ainsi toute information de localisation temporelle, les fonctions de base de la CWT sont des versions mises à l'échelle et décalées de l'ondelette mère localisée dans le temps. La CWT est utilisée pour construire une représentation temps-fréquence d'un signal qui offre une très bonne localisation temporelle et fréquentielle.
Le CWT est un excellent outil pour cartographier les propriétés changeantes des signaux non stationnaires. Le CWT est également un outil idéal pour déterminer si un signal est stationnaire ou non au sens global. Lorsqu'un signal est jugé non stationnaire, la CWT peut être utilisée pour identifier les sections stationnaires du flux de données.
Les calculs de base dans les procédures CWT de FlexPro suivent généralement les algorithmes de Torrence et de Compo tels qu'énumérés dans la section des références ci-dessous. La nomenclature utilisée dans les équations ci-dessous suit également celle utilisée dans l'article de Torrence et Compo.
Transformée en Ondelette Continue
Les définitions du CWT sont les suivantes :
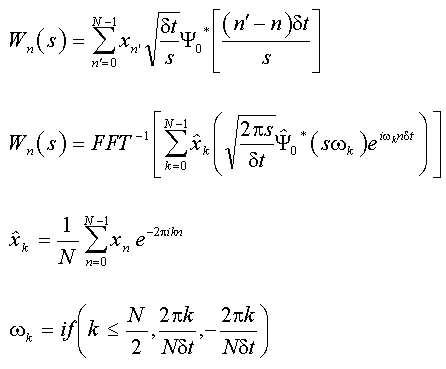
La CWT est une convolution de la séquence de données avec une version mise à l'échelle et traduite de l'ondelette mère, la fonction Ψ. Cette convolution peut être réalisée directement, comme dans la première équation, ou via la convolution rapide basée sur la FFT dans la deuxième équation.
Notez que la CWT est une fonction continue, sauf pour la série de données discrètes x et sa transformée de Fourier discrète. Dans ces équations, * symbolise une conjugaison complexe, N est la longueur de la série de données, s est l'échelle d'ondelette, δt est l'intervalle d'échantillonnage, n est l'indice de temps localisé et ω est la fréquence angulaire. Chacune des équations contient une normalisation afin que la fonction ondelette contienne une énergie unitaire à chaque échelle.
Dans la CWT, pour chaque valeur de l'échelle utilisée, la corrélation entre l'ondelette mise à l'échelle et les segments successifs du flux de données est calculée. À moins qu'une reconstruction ne soit nécessaire, il n'y a aucune restriction dans le CWT quant au nombre d'échelles utilisées, ni quant à l'espacement entre les échelles. Un spectre CWT peut utiliser des échelles linéaires ou logarithmiques de toute densité souhaitée. Si nécessaire, un spectre haute résolution peut être généré pour une gamme étroite de fréquences. Les convolutions peuvent être faites jusqu'à N fois à chaque échelle, et doivent être faites toutes les N fois si la FFT est utilisée. Le CWT est constitué de N valeurs spectrales pour chaque échelle utilisée, chacune d'entre elles nécessitant une FFT inverse. La charge de calcul du CWT et ses besoins en mémoire sont donc considérables. L'avantage de cette mesure élevée de redondance dans le CWT est un spectre temps-fréquence précis.
Fonctions de base des ondelettes (ondelettes mères)
Contrairement à une décomposition de Fourier qui utilise toujours des fonctions de base exponentielles complexes (sinus et cosinus), une décomposition en ondelettes utilise une fonction oscillatoire localisée dans le temps comme ondelette d'analyse ou ondelette mère. L'ondelette mère est une fonction continue en temps et en fréquence qui sert de fonction source à partir de laquelle sont construites les fonctions de base mises à l'échelle et translatées. L'ondelette mère peut être complexe ou réelle, et elle comprend généralement un paramètre réglable qui contrôle les propriétés de l'oscillation localisée. L'analyse en ondelettes est plus compliquée que l'analyse de Fourier car il faut spécifier complètement l'ondelette mère à partir de laquelle les fonctions de base seront construites. FlexPro propose trois ondelettes mères différentes, chacune en version complexe et en version à valeur réelle.
Morlet Wavelet
L'ondelette CWT la plus couramment utilisée est l'ondelette de Morlet, une sinusoïde complexe à fenêtre gaussienne qui est définie comme suit dans les domaines temporel et fréquentiel :
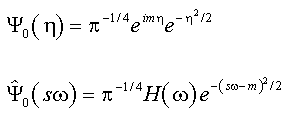
Dans ces équations, η est un paramètre temporel non dimensionnel, m est le nombre d'onde et H est la fonction de Heaviside.
Dans le tracé temporel qui suit, les composantes réelles et complexes d'une ondelette de Morlet avec un paramètre ajustable m (nombre d'onde) de 6 sont représentées :
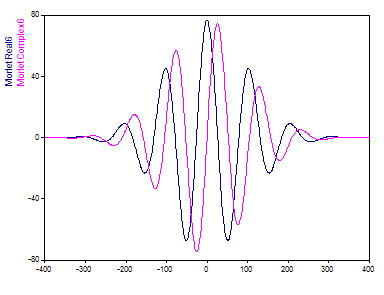
Le paramètre ajustable de l'ondelette de Morlet, le nombre d'onde, peut varier de 6 à 100 dans FlexPro. Une ondelette de Morlet avec un paramètre ajustable de 20 a une représentation très différente dans le domaine temporel :
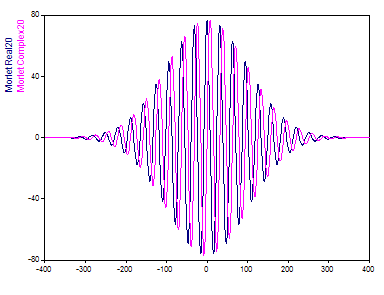
Le nombre d'oscillations de l'ondelette de Morlet est approximativement celui du nombre d'onde.
Paul Wavelet
FlexPro propose également l'ondelette de Paul :
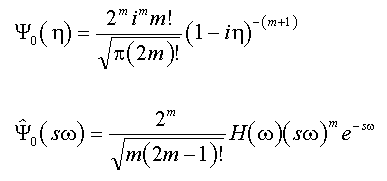
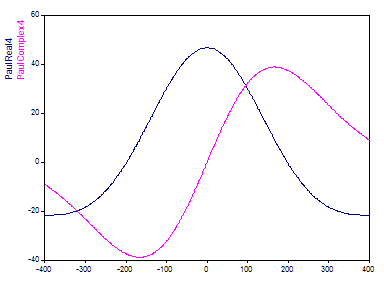
L'ondelette de Paul décroît plus rapidement (comme la racine carrée d'une fonction factorielle). Le paramètre ajustable de l'ondelette de Paul est un ordre qui peut varier de 4 à 40 dans FlexPro. À un ordre de 4, une seule oscillation existe dans l'ondelette :
Même au plus grand ordre soutenu de 40, l'ondelette de Paul présente à peu près les mêmes oscillations que l'ondelette de Morlet à son plus petit nombre d'onde :
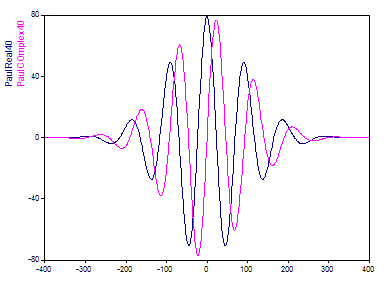
L'ondelette de Paul offre une meilleure localisation temporelle que la Morlet en raison de sa décroissance plus rapide dans le domaine temporel. Cependant, contrairement au Morlet, sa représentation de Fourier n'est pas un pic symétrique mais plutôt un pic décalé vers la droite en direction des hautes fréquences. Elle suit approximativement une forme de pic gamma, et devient moins asymétrique à mesure que les ordres augmentent. Même à l'ordre le plus élevé de Paul, à savoir 40, un déséquilibre important vers la droite est évident dans son pic dans le domaine des fréquences. L'ondelette de Paul offre donc une moins bonne résolution en fréquence.
Dérivée Ondelette Gaussienne
La troisième ondelette mère prise en charge est la GaussDeriv (dérivée gaussienne). La composante réelle est définie comme suit :
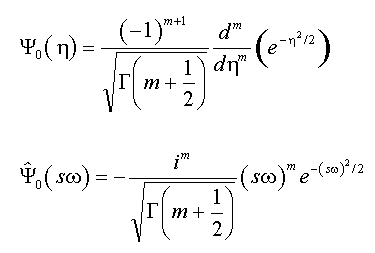
L'ondelette complexe est générée par l'addition d'une fonction de Heaviside dans le domaine des fréquences. Cette ondelette décroît avec la racine carrée de la fonction gamma. Sa localisation temporelle se situe entre celle des ondelettes de Morlet et de Paul. Le paramètre ajustable de l'ondelette GaussDeriv est l'ordre de dérivation qui peut varier de 2 à 80 dans FlexPro. La dérivée la plus basse, 2, est connue comme l'ondelette de Marr ou Mexican Hat. Une seule oscillation est contenue dans l'ondelette :
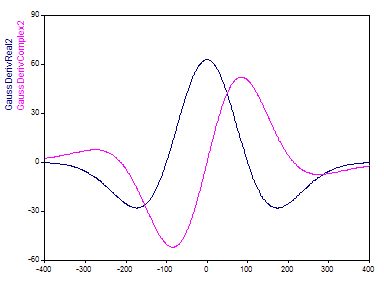
À son plus grand paramètre réglable supporté de 80, l'ondelette GaussDeriv contient à peu près le même nombre d'oscillations que l'ondelette Morlet avec un nombre d'onde de 12 :
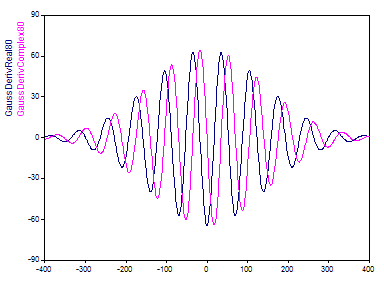
Représentation dans le domaine fréquentiel
La transformée dans le domaine fréquentiel des ondelettes mères (onde de Morlet numéro 6, onde de Paul ordre 40, et dérivée gaussienne ordre 20) est la suivante :
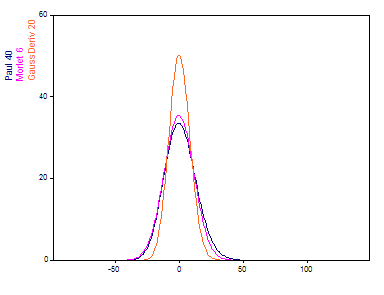
Lorsque les paramètres ajustables de chacune des trois ondelettes mères sont réglés pour produire environ six oscillations, l'ondelette dérivée gaussienne produit les informations spectrales les plus compactes dans le domaine des fréquences. L'ondelette de Paul produit le moins compact. L'ondelette de Morlet est entre.
La transformée de Fourier d'une ondelette de Morlet produit un pic symétrique dans le domaine des fréquences. La représentation dans le domaine des fréquences de l'ondelette GaussDeriv est exactement une forme de pic gamma. L'asymétrie décalée vers la droite du pic de fréquence est sensiblement inférieure à celle de Paul, et disparaît essentiellement au-dessus de l'ordre de dérivation 20 environ (des valeurs plus élevées pour la dérivée de l'ondelette GaussDeriv produisent des pics de fréquence presque gaussiens).
Résolution temporelle par rapport à la résolution fréquentielle
Les trois bases d'ondelettes sont supportées de manière compacte, ce qui signifie que les oscillations sont effectivement localisées dans le temps par des décroissances rapides. Pour un nombre donné d'oscillations dans l'ondelette, l'ondelette de Paul localise le plus efficacement dans le domaine temporel. L'ondelette Morlet est légèrement moins efficace, et l'ondelette dérivée gaussienne est la moins efficace des trois. Cependant, en comparant les résolutions de fréquence, l'ondelette dérivée gaussienne est la meilleure et l'ondelette de Paul est la moins bonne. La qualité de l'ondelette de Morlet se situe entre les deux.
Bien que l'ondelette de Morlet ne soit pas aussi compacte que la dérivée gaussienne pour un nombre donné d'oscillations dans l'ondelette, elle est capable de générer un nombre beaucoup plus élevé d'oscillations avec les plages de réglage prises en charge par FlexPro. Ainsi, une plus grande résolution de fréquence peut être obtenue en utilisant l'ondelette de Morlet.
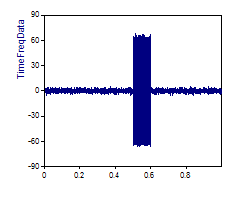
Cela peut être mieux illustré par un graphique. Les analyses en ondelettes suivantes utilisent un ensemble de données bruitées où une seule oscillation sinusoïdale se produit entre 0,5 et 0,6 temps :
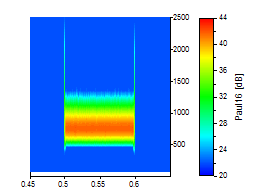
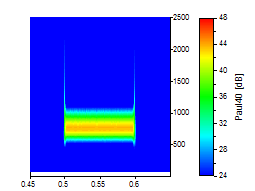
Le pic de l'ondelette a été agrandi pour illustrer ce compromis entre résolution temps-fréquence. Tous les graphiques utilisent la même échelle temps-fréquence. Les trois premiers graphiques sont pour le Morlet à des nombres d'onde de 6, 20 et 50 :
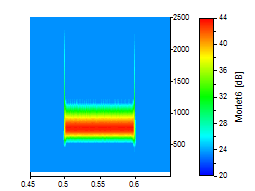
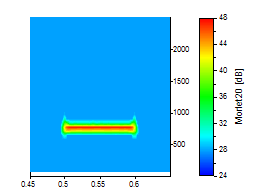
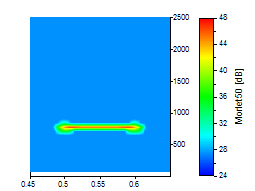
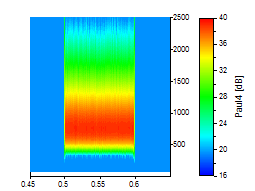
Les trois suivants sont pour l'ondelette de Paul aux ordres de 4, 16 et 40 :
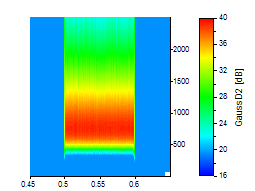
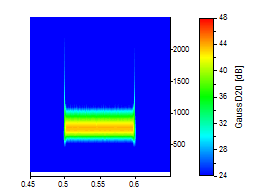
Les trois derniers sont pour l'ondelette Gausssian Derivative aux ordres 2, 20 et 80 :
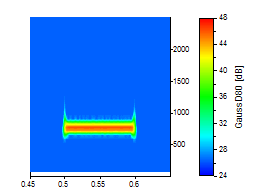
En général, à moins que vous n'ayez besoin de la meilleure localisation temporelle possible, l'ondelette de Morlet suffira probablement puisqu'elle offre une très bonne résolution à la fois en temps et en fréquence.
Sa résolution en fréquence est respectable, même pour les nombres d'onde les plus faibles. La résolution en fréquence de l'ondelette de Paul à son meilleur (ordre 40) est proche de celle de Morlet avec son nombre d'onde le plus faible de 6. Vous pouvez également voir l'asymétrie de fréquence dans chacun des exemples de Paul. Cependant, si vous avez besoin de la meilleure localisation temporelle possible, l'ondelette de Paul est un bon choix.
L'ondelette GaussDeriv à sa meilleure résolution en fréquence (ordre 80) est proche de la Morlet avec un nombre d'onde de 12. Contrairement à l'ondelette de Paul, les ordres supérieurs de l'ondelette de Gauss-Deriv sont essentiellement symétriques, et ils peuvent dépasser la résolution en fréquence de l'ondelette de Morlet avec des nombres d'onde plus faibles.
Analyse multirésolution
Pour la Transformée de Fourier à court terme, une taille de segment de largeur fixe contrôle le compromis de résolution temps-fréquence. Il en résulte une résolution unique en temps et une résolution unique en fréquence, quelle que soit la fréquence restituée. En revanche, l'analyse en ondelettes est une méthode multirésolution. La résolution temps-fréquence n'est pas constante, mais varie avec la fréquence. L'analyse multirésolution a été conçue pour la condition commune où les composantes de haute fréquence existent pour de courtes durées dans un signal, et les composantes de basse fréquence sont plus persistantes.
Les composantes haute fréquence à courte durée de vie nécessitent une forte localisation temporelle. Pour y parvenir, la résolution en fréquence des composants haute fréquence sera diminuée. D'autre part, les composantes basse fréquence à longue durée de vie peuvent tolérer une résolution temporelle plus faible, mais nécessitent une résolution fréquentielle efficace. Les composantes de basse fréquence déterminent souvent la majeure partie du caractère d'un signal, et ces propriétés seront mieux quantifiées si la résolution en fréquence est aussi fine que possible.
L'analyse multirésolution permet d'éviter le difficile problème de la détermination d'une largeur de segment optimale. La largeur des segments de temps varie automatiquement avec la fréquence. L'inconvénient évident est qu'il est possible qu'un signal contienne des composantes de basse fréquence à court terme ou des composantes de haute fréquence à long terme. Pour de tels signaux, la transformée de Fourier à temps court est probablement un meilleur choix que l'analyse par ondelettes. En outre, cette variation de la résolution en fréquence rend impossible la lecture directe des puissances ou des amplitudes spectrales à partir d'un spectre d'ondelettes. Il s'agit d'un autre cas où l'analyse à résolution unique de la transformée de Fourier à temps court peut être préférable.
L'ensemble de données suivant est constitué de sinusoïdes séquentielles de puissance égale dans un bruit blanc à 1%. Entre les temps 0.01 et 0.04, une sinusoïde de fréquence 250 est présente. Pour les temps 0,06 à 0,09, une sinusoïde de fréquence 500 Hz est présente, pour les temps 0,11 à 0,14, une sinusoïde de fréquence 1000 Hz comprend le signal, et pour les temps 0,16 à 0,19, une sinusoïde de fréquence 2000 Hz est présente.
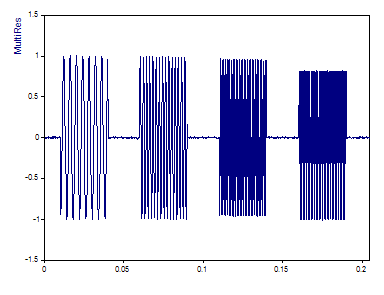
Dans le spectre CWT qui suit, l'ondelette de Morlet avec un nombre d'onde de 12 est utilisée pour générer un spectre CWT :
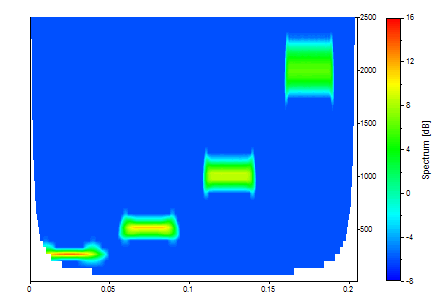
L'analyse multirésolution est évidente. La composante de fréquence de 250 Hz est superbement localisée en fréquence, mais est très floue dans le temps. Inversement, la composante de fréquence de 2000 Hz est bien définie dans le temps, mais assez floue en fréquence.
Comparez le spectre CWT avec un STFT optimisé. La résolution unique dans la STFT est facilement visible :
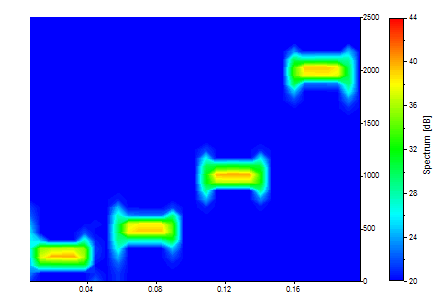
Zero Padding et le cône d'influence
Le spectre CWT est calculé en prenant d'abord une transformée de Fourier discrète de la série de données. Ensuite, pour chaque échelle (fréquence spécifiée) du spectre, la réponse en fréquence de l'ondelette fille est calculée analytiquement, puis multipliée par la transformée en fréquence des données et le produit est inversé.
Les transformées de Fourier supposent des données périodiques. Pour que la convolution rapide de la FFT soit exempte des effets d'enveloppement qui résultent de la non-périodicité à la fois des données et de la fonction de réponse (ondelette fille), il faut un rajout de zéro (zero padding) égal à la moitié de la longueur des éléments non nuls dans la réponse en fréquence de l'ondelette fille.
Cette longueur varie en fonction de l'échelle (fréquence). Un rajout de zéro (zero padding) égal à deux fois la taille des données garantit qu'aucun effet d'enveloppement n'est possible dans le spectre. Souvent, il est possible d'effectuer un rajout de zéro (zero padding) à la puissance 2 suivante et d'obtenir des effets d'enveloppement négligeables ainsi que les performances FFT les plus rapides.
Lorsque le rajout de zéro (zero padding) est suffisant, l'effet d'enveloppement est éliminé, mais un autre problème se pose. Avec un rajout de zéro (zero padding), il est probable qu'une discontinuité soit introduite à la fin du flux de données. De plus, la puissance est réduite près des bords du spectre avec l'introduction des zéros dans la convolution.
Cette zone d'effets de bord est connue sous le nom de cône d'influence (COI). Dans FlexPro, aucune information spectrale dans la zone d'influence n'est affichée. L'information spectrale à l'intérieur du cône d'influence n'est pas susceptible d'être exacte, que l'on utilise ou non le rajout de zéro (zero padding). S'il n'est pas utilisé, des effets d'enveloppement peuvent se produire aux basses fréquences. Si elle est utilisée, les puissances spectrales peuvent être diminuées.
Le cône d'influence est calculé en utilisant les distances de pliage électronique selon la référence de Torrence et Compo.
Les ondelettes orthogonales et la DWT
La plupart des analyses en ondelettes utilisent une paire de filtres pour isoler successivement les composantes passe-bas et passe-haut d'un signal. C'est ce qu'on appelle la transformée en ondelettes discrètes (DWT). Les ondelettes DWT ne sont pas des fonctions continues du temps et leurs transformées ne sont pas une fonction continue de la fréquence. Il s'agit plutôt d'ensembles de coefficients de filtre dans le domaine temporel qui produisent généralement une base orthogonale qui simplifie grandement le filtrage et la reconstruction des données. Un DWT est non redondant. Le nombre de blocs de puissance d'ondelette à chaque échelle est une fonction de la largeur d'ondelette sans chevauchement. Dans une DWT typique, les fréquences sont espacées à des puissances unitaires de deux et le nombre de blocs dans le temps augmentera par des puissances unitaires de deux à mesure que ces fréquences fixes augmentent. Bien que la DWT soit rapide et que sa représentation temps-fréquence d'un signal ne nécessite qu'une mémoire modeste, elle n'est pas pratique pour l'analyse spectrale temps-fréquence.
FlexPro utilise exclusivement le CWT pour l'analyse spectrale temps-fréquence. Les algorithmes CWT offrent une plus grande précision, bien que cela se fasse au détriment de la charge de calcul et de l'utilisation de la mémoire.
Références
Pour ceux qui souhaitent comprendre les subtilités de l'application de l'analyse par ondelettes à des données du monde réel, il existe un article bien écrit qui couvre le CWT de manière approfondie et accessible :
•Christopher Torrence and Gilbert Compo, "A Practical Guide to Wavelet Analysis", Bulletin of the American Meteorological Society, v.79, no.1, p.61-78. January 1998
Cette référence explique le CWT dans le contexte de l'analyse des données des séries chronologiques d'El Nino. Les auteurs ont également publié un paquetage FORTRAN d'analyse des ondelettes CWT du domaine public, WAVEPACK. Le code WAVEPACK est disponible sur Internet à l'adresse suivante : http://paos.colorado.edu/research/wavelets/
Voir aussi
Objet d'analyse Spectre temps-fréquence - Spectre de la transformée en ondelettes continues (CWT)
Vous serez probablement intéressé par les articles suivants :
Vous êtes actuellement en train de consulter le contenu d'un espace réservé de Facebook. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous devez charger le contenu de reCAPTCHA pour soumettre le formulaire. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de Instagram. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de X. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informations