Das Analyseobjekt Umdrehungssynchrone Ordnungsanalyse berechnet eine Ordnungsanalyse für drehzahlabhängige Schwingungen. An rotierenden Maschinen gemessene Vibrationen zeigen ein Spektrum, in dem Maxima bei Frequenzen auftreten, die einem Vielfachen der Drehzahl der Maschine entsprechen. Für das Auftreten dieser Maxima gibt es zwei verschiedene Ursachen. Einerseits kann man die Maschine als nicht-lineares Übertragungssystem betrachten, welches mit einer der Drehzahl entsprechenden, harmonischen Schwingung angeregt wird. Die Nicht-Linearität erzeugt Oberwellen dieser Grundschwingung, welche zu entsprechenden Maxima führen. Andererseits kann eine solche Maschine Komponenten enthalten, deren Drehzahl nicht gleich der Grunddrehzahl ist, aber immer einem festen Vielfachen dieser Drehzahl entspricht. So haben z. B. verschiedene Wellen in einem Getriebe unterschiedliche Drehzahlen. Aber auch die Zähne eines Zahnrades oder die Kugeln in einem Kugellager erzeugen Vibrationen, die in fester Relation zur Drehzahl stehen. Kennt man dieses als Ordnung bezeichnete Verhältnis aus Grundfrequenz einer Komponente zur Grundfrequenz der Maschine, dann lassen sich einzelne Maxima im Spektrum gezielt einer einzigen oder wenigen Komponenten der Maschine zuordnen. Hiermit kann z. B. die Ursache von Resonanzen isoliert werden.

Bei dem hier eingesetzten Verfahren wird zunächst eine Abtastratenumwandlung des Zeitsignals durchgeführt (umdrehungssynchrone Umabtastung), so dass das Signal nicht mehr in zeitlich äquidistanten Schritten, sondern in äquidistanten Drehwinkelschritten (d.h. äquidistanten Umdrehungsintervallen) vorliegt. Dies erlaubt auf effektive Weise die Durchführung einer Ordnungsanalyse, da das Frequenzspektrum (d.h. die Fourier-Transformation) des in den Umdrehungsbereich konvertierten Signals dann unmittelbar das sogenannte Ordnungsspektrum liefert (Details siehe RevolutionSyncSampling):

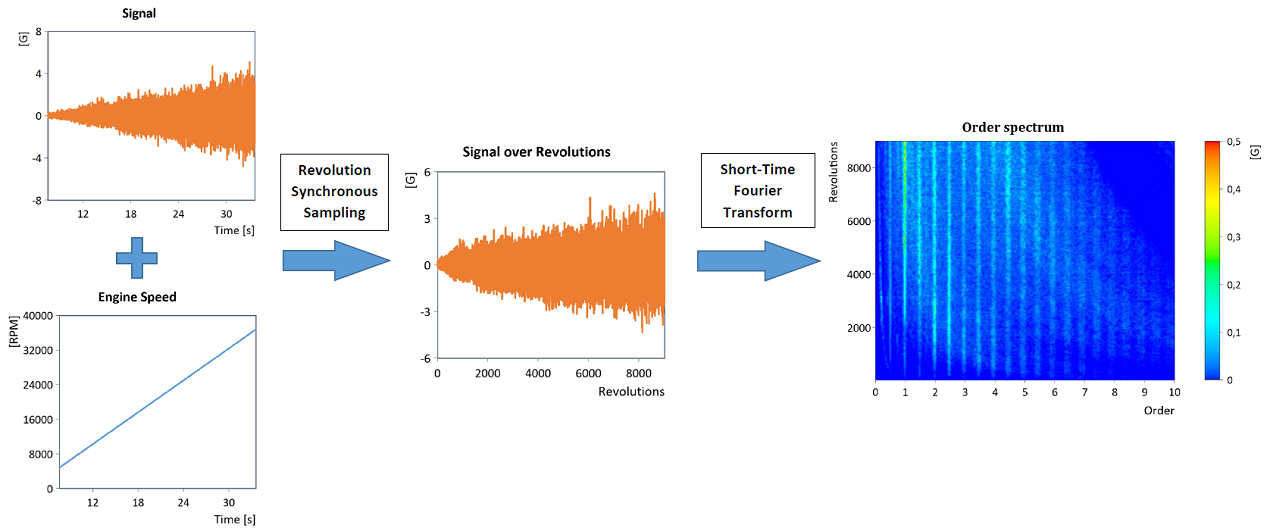
Die Ordnungsverläufe erhält man anschließend aus dem Ordnungsspektrum durch Extraktion der einzelnen Ordnungslinien (Ordnungsschnitte).

Zur Ordnungsanalyse werden vorwiegend zwei Messverfahren angewendet. Bei einem Hochlauf, werden die Vibration und die Momentandrehzahl synchron gemessen, während die Maschine gewöhnlich langsam von ihrer Mindest- zu ihrer Maximaldrehzahl hochgefahren wird (Hochlaufanalyse). Bei einem zweiten Verfahren wird die Maschine zunächst auf eine bestimmte Drehzahl gebracht und dann wird für diese Drehzahl eine Messung der Vibration durchgeführt (Ordnungsanalyse mit konstanter Drehzahl). Das Analyseobjekt Umdrehungssynchrone Ordnungsanalyse unterstützt beide Varianten. Zudem ist die Ordnungsanalyse mittels umdrehungssynchroner Umabtastung äußerst flexibel und lässt sich sogar für verrauschte sowie nicht-monotone Drehzahldatensätze durchführen (Ordnungsanalyse mit variabler Drehzahl).

Registerkarte Daten

Diese Registerkarte spezifiziert die Eingangsdaten und die Parameter zur Transformation vom Zeit- in den Umdrehungsbereich (Details siehe auch RevolutionSyncSampling):.

Signale im Zeitbereich

Das für das Analyseobjekt zu analysierende Zeitsignal muss in der Datenstruktur Signal vorliegen. Die Drehzahl kann entweder in der Datenstruktur Signal (entspricht einer Hochlaufanalyse oder einer Ordnungsanalyse mit variabler Drehzahl) oder als Einzelwert (entspricht Ordnungsanalyse mit konstanter Drehzahl oder zu fester Grundfrequenz) angegeben werden.

Bei fehlenden Einheiten oder ausgeschalteter Einheitenverwaltung, wird die Drehzahl stets in der Einheit [1/min] und die X-Komponente des Zeitsignals in der Einheit interpretiert.

Die Momentandrehzahl wird oft mit einem Impulsgeber gemessen, der eine bestimmte Anzahl von Impulsen pro Umdrehung erfasst. Sie können das hieraus resultierende Impulssignal direkt in ein Drehzahlsignal konvertieren. Markieren Sie hierzu die Option Drehzahl ist Impulssignal und geben Sie die Anzahl der Impulse pro Umdrehung an. Die Konvertierung des Impulssignals in ein Drehzahlsignal erfolgt mit der ImpulseToFrequency-Funktion.

Umabtastung in den Umdrehungsbereich

Zur Umabtastung vom Zeit- in den Umdrehungsbereich stehen drei verschiedene Modi zur Verfügung. In den meisten praktischen Anwendungsfällen ist die lineare Umabtastung ausreichend:

Bei Wahl des Splines- oder des FFT-Resampling-Verfahrens, muss ein Resample-Faktor spezifiziert werden, um den die Abtastrate des Signals beim Transformationsalgorithmus erhöht wird.

Unabhängig vom gewählten Resample-Verfahren, sind die Anzahl der Datenpunkte pro Umdrehung für das in den Umdrehungsbereich zu transformierenden Signals anzugeben. Dies bestimmt die Abtastung des transformierten Signals im Umdrehungsbereich. Gemäß Nyquist-Abtasttheorem bestimmt die Hälfte dieses Wertes die maximal Ordnung, die mittels Fourier-Analyse im Ordnungsspektrum berechnet werden kann.

Zur Bestimmung der Anzahl der Datenpunkte pro Umdrehung stehen zwei Modi zur Verfügung:

Trendkorrektur (Umdrehungsbereich)

In vielen Anwendungsbeispielen führt ein vorhandener, zu großer DC-Offset zu einer visuell ungeeigneten Darstellung im Konturplot des Ordnungsspektrums, in welcher der DC-Anteil dominiert. Es ist daher vorteilhaft, den DC-Anteil herauszufiltern. Hierzu lässt sich für das in den Umdrehungsbereich transformierte Signal ein entsprechender DC-Offset-Hochpassfilter mit einstellbarer Grenzfrequenz (Abschneide-Ordnung) und Filterordnung (Filtersteilheit) einstellen (Details zum DC-Offset-Hochpassfilter siehe DCRemovalFilter-Funktion).

Registerkarte Optionen

In dieser Registerkarte wird das berechnete Ordnungsspektrum bzw. die Ordnungsschnitte (Extraktion der Ordnungslinien aus dem Ordnungsspektrum) spezifiziert. Das Ordnungsspektrum ergibt sich hierbei durch klassische Frequenzanalyse mit Hilfe der STFTSpectrum-Funktion des in den Umdrehungsbereichs transformierten Signals (d.h. für jeweils überlappende Datensegmente wird eine Fourier-Analyse durchgeführt). Mit Hilfe der OrderCuts-Funktion werden die Ordnungsschnitte berechnet, d.h. die Ordnungslinien aus dem Ordnungsspektrum ausgeschnitten.

Ausgabe

Es stehen die folgenden vier Ausgabemodi der (umdrehungssynchronen) Ordnungsanalyse zur Verfügung:

Spektrumtyp und Auflösung

Das Ordnungsspektrum kann in einer Vielzahl von Formaten berechnet und ausgegeben werden. Die Spektrumtypen entsprechen den Spektrumtypen des Analyseobjekts Zeit-Frequenz Spektralanalyse (siehe auch STFTSpectrum-Funktion).

Bei der Amplitudendarstellung sehen Sie die Amplituden, in der RMS-Darstellung die RMS-Beiträge der einzelnen Ordnungen. Bei der normierten dB-Darstellung befindet sich der höchste Peak bei 0dB, ein Peak bei -3dB hätte die halbe Leistung und ein Peak bei -6dB hätte die halbe Amplitude. Das Feld Maximaler dB-Bereich wird nur für die Formate dB und dB, normiert aktiviert und eingeblendet. Die dB-Beschränkung wirkt sich auf die Endwerte der automatischen Skalierung und damit auch auf den Farbverlauf im Spektrogramm aus. Bitte geben Sie 0 in dieses Feld ein, um einen unbeschränkten Bereich zu erhalten. Bei der Ordnungsanalyse wird gewöhnlich RMS als Spektrumtyp gewählt (Default-Einstellung).

Die Qualität des Ordnungsspektrums hängt entscheidend von der Wahl der Größe jedes Datensegments, Segmentlänge, und dem Betrag der Überlappung, Überlappung %, ab. Die Segmentlänge ist hierbei durch die einstellbare Ordnungsauflösung eindeutig festgelegt (z.B. eine Ordnungsauflösung von 1/32 ergibt eine Segmentlänge von 32 * Anzahl Datenpunkte pro Umdrehung). Segmentlänge und Ordnungsauflösung sind also antiproportional. Eine hohe Redundanz wird allgemein empfohlen. Die Segmentlänge sollte so klein wie möglich sein, um eine hohe Umdrehungs-/Zeit-/Drehzahlauflösung zu erzielen, und so groß wie nötig sein, um eine hohe Ordnungsauflösung zu erzielen. Dieser Kompromiss ist beim Arbeiten mit der STFT immer gegenwärtig. Zur Erhöhung der Redundanz und Verbesserung der Qualität des Ordnungsspektrum kann eine prozentuale Überlappung der Datensegmente eingestellt werden. Die Umdrehungs-/Zeit-/Drehzahlauflösung wird dadurch erhöht, die Ordnungsauflösung bleibt gleich.

Bei der Einstellung Lücke in Anzahl Umdrehungen bleiben Daten unberücksichtigt. Diese Einstellung sollte nur für sehr lange Zeitreihen mit sich langsam änderndem Spektralgehalt gewählt werden.

Bemerkungen zum Speicherbedarf: Für die STFT werden separate FFTs für jedes Datensegment berechnet und gespeichert. Um den Speicherbedarf gering zu halten, sollten Sie hohe Überlappungswerte vermeiden, weil sich hierdurch die Segmentanzahl drastisch erhöht. Die Segmentanzahl hängt nicht linear von der Überlappung ab und steigt ab Werten von ca. 70% stark an. Obwohl FlexPro Überlappungen von bis zu 95% zulässt, ergeben Werte über 50 bis 70% normalerweise wenig Gewinn.

Fenster

FlexPro bietet eine Vielzahl von Bewertungsfenstern, um den Leckeffekt zu verringern. Die hohe Redundanz, die durch eine Überlappung der Fenster erreicht werden kann, kompensiert den Informationsverlust, der durch Unterdrückung der Daten an den Rändern jedes Fensters entsteht. Die Fensterbewertung führt zu einer schärferen Ausprägung der Spektrallinien im Ergebnis. Die Amplituden des Spektrums sowie die Leistung werden jedoch auch vermindert.

In der Auswahlliste Normierung stehen Ihnen daher zwei Auswahlmöglichkeiten zur Normierung nach der Fensterbewertung zur Verfügung. Bei Auswahl von Amplitude wird auf den Gewinn der verwendeten Fensterfunktion normiert, d. h. die Summe aller Werte der Fensterfunktion, dividiert durch deren Anzahl. Dies kompensiert die durch die Fensterbewertung der Daten erfolgende Dämpfung der Amplituden und eignet sich besonders zum Ausmessen von Peaks im Ordnungsspektrum. Wenn Sie Leistung wählen, wird der Leistungsverlust kompensiert, d. h. es wird das Verhältnis der Summe der Quadrate der Daten vor und nach der Fensterbewertung als Normierungsfaktor verwendet. Die Gesamtenergie im Ordnungsspektrum entspricht hiermit immer der der Daten vor der Fensterbewertung.

Das Feld Breitenanpassung wird zum Festlegen der spektralen Breite, und damit des Dynamikbereichs, der anpassbaren Fenster verwendet. Für Fenster mit fester Breite ist dieses Feld deaktiviert.

Ergebnis des Ordnungsspektrum

Bei Wahl des Ausgabemodus Ordnungsspektrum, sind die folgenden Ergebnistypen auswählbar.

Beispiel eines RMS-Ordnungsspektrums eines Hochlaufs (mit Y = Amplitude, X = Ordnung, Z = Drehzahl):

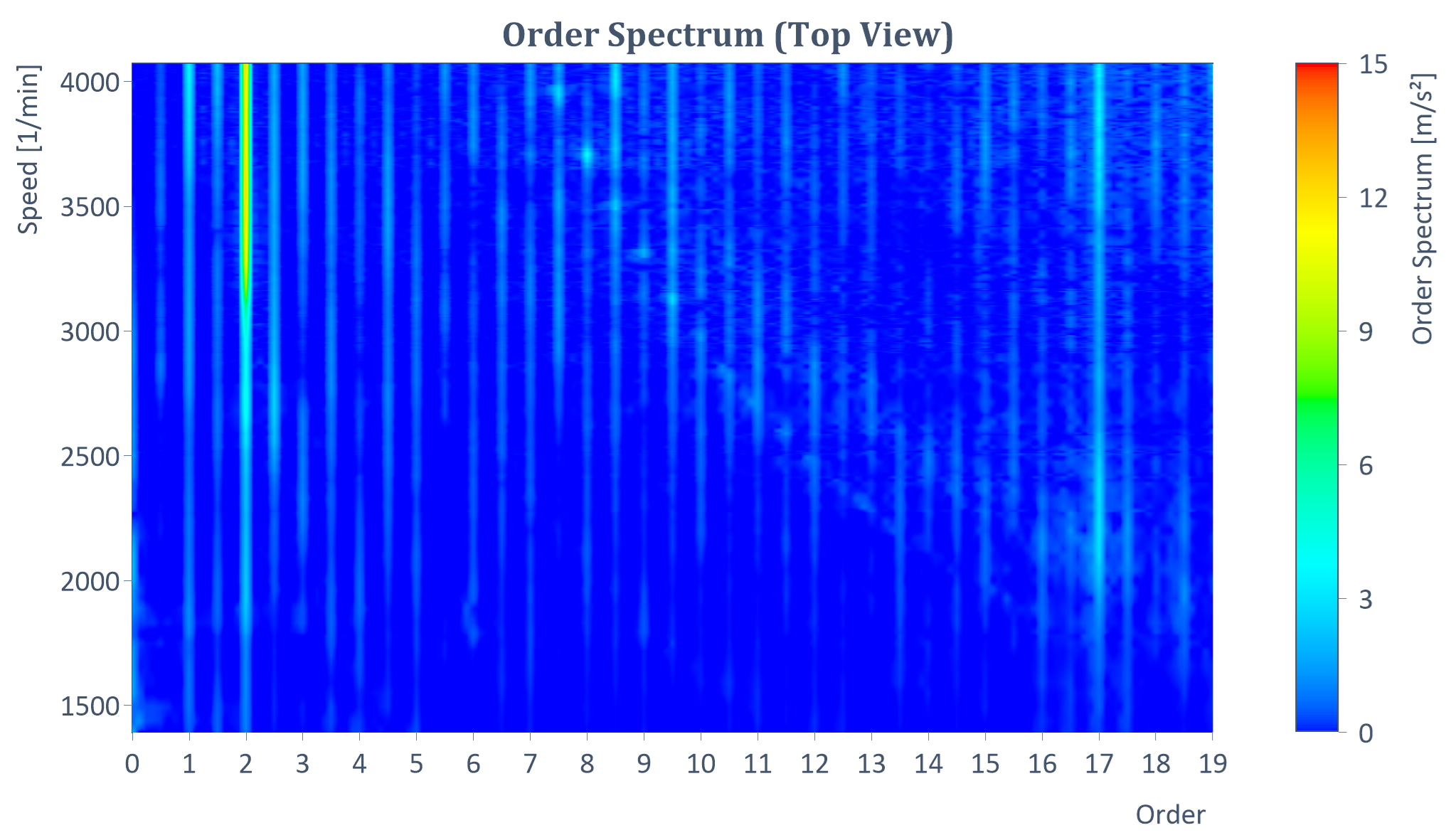
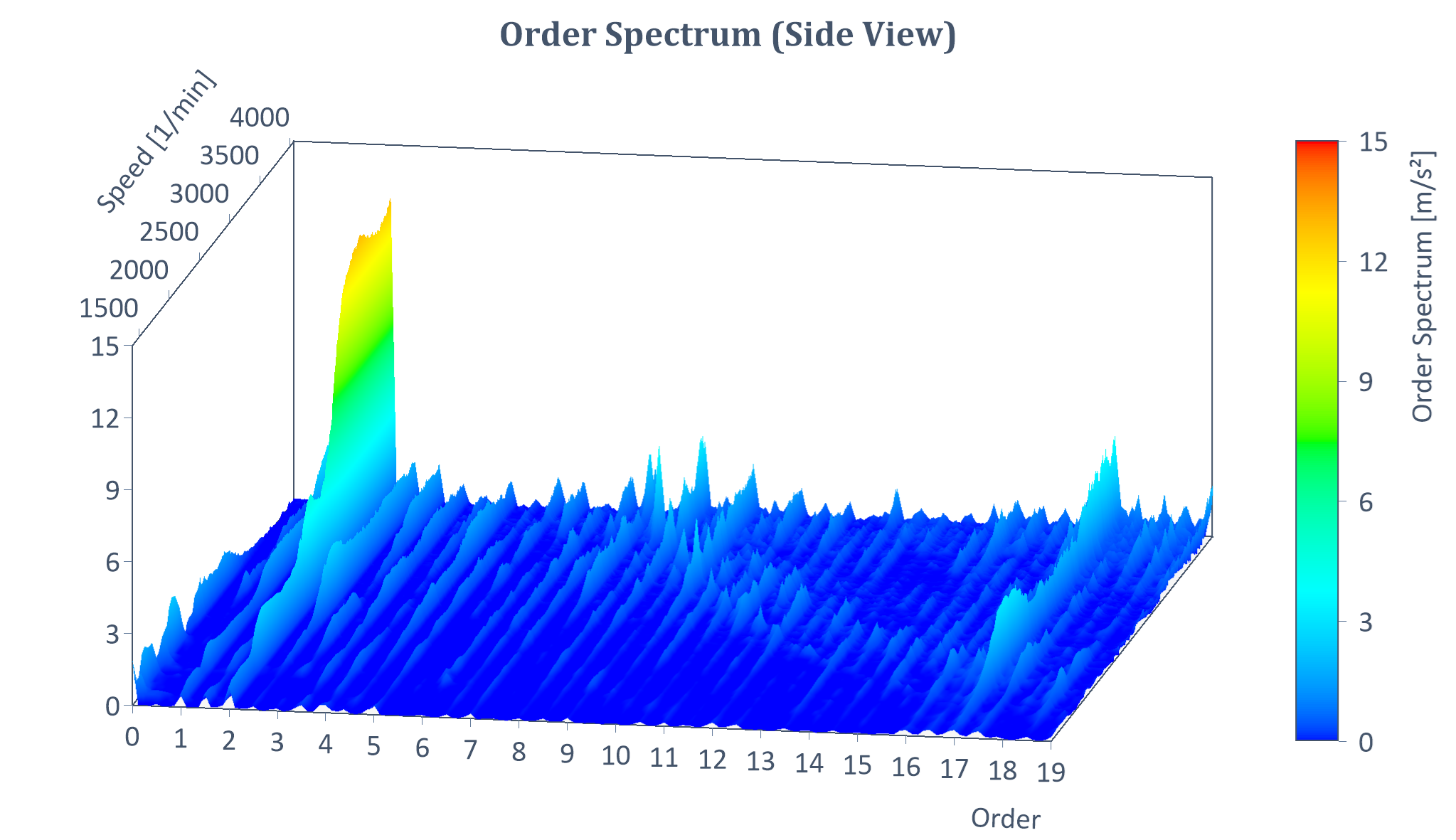
Ergebnis der Ordnungsschnitte (als Liste)

Bei Wahl des Ausgabemodus Ordnungen aus Ordnungsspektrum extrahieren (als Liste), sind die folgenden Ergebnistypen auswählbar.

Bei Berechnung von Ordnungsschnitten über der Drehzahl, enthält das Ergebnis nicht-äquidistante Drehzahlstützpunkte (diese entsprechen exakt den äquidistanten Umdrehungsstützpunkten nach Berechnung des Ordnungsspektrums im Umdrehungsbereich). Das Ergebnis kann daher zusätzlich über einem äquidistanten Drehzahlbereich mit festzulegender Startdrehzahl, Enddrehzahl und Drehzahlschrittweite ausgewertet werden. Hierbei erfolgt eine lineare Interpolation über dem angegebenen äquidistanten Drehzahlbereich. Damit die lineare Umabtastung sinnvolle Resultate ergibt, sollte die vom Algorithmus berechnete Drehzahlauflösung ausreichend hoch sein (z.B. möglichst große Überlappung in % der Datensegmente und/oder ausreichend kleine Ordnungsauflösung).

Ergebnis der Ordnungsschnitte (als Signalreihe)

Bei Wahl des Ausgabemodus Ordnungen aus Ordnungsspektrum extrahieren (als Signalreihe), sind die folgenden Ergebnistypen auswählbar.

Analog wie zuvor beschrieben, kann das Ergebnis bei Berechnung von Ordnungsschnitten über der Drehzahl über einem äquidistanten Drehzahlbereich ausgewertet werden.

Ordnungen und Bandbreiten

Sofern Ordnungsschnitte berechnet werden (oder zur Berechnung der gemittelten RMS-Ordnungsschnitte verwendet werden, s.u.), können die zu analysierenden Ordnungen in einer Tabelle explizit eingestellt oder aus einem Datensatz entnommen werden. Zur Extraktion dieser Ordnungen aus dem Ordnungsspektrum stehen die folgenden drei Modi zur Verfügung:

Bemerkung: Gewöhnlich wird in den meisten Anwendungsfällen der dritte Modus, d.h. die energetisch korrekte Extraktion durch Berechnung des RMS-Pegel im eingestellten Ordnungsband, verwendet. Dies ist die Standardeinstellung zur Berechnung der Ordnungsschnitte. Das Ergebnis entspricht anschaulich dem RMS-Verlauf des in dem eingestellten Ordnungsband bandpassgefilterten Signals. Der gleichen RMS-Verlauf der jeweiligen Ordnung lässt sich demnach alternativ und äquivalent ebenso mit Hilfe des Analyseobjekt Ordnungsfilter berechnen.

Beispiel von RMS-Ordnungsschnitten (als Liste) eines Hochlaufs (mit Y = Amplitude, X = Drehzahl):

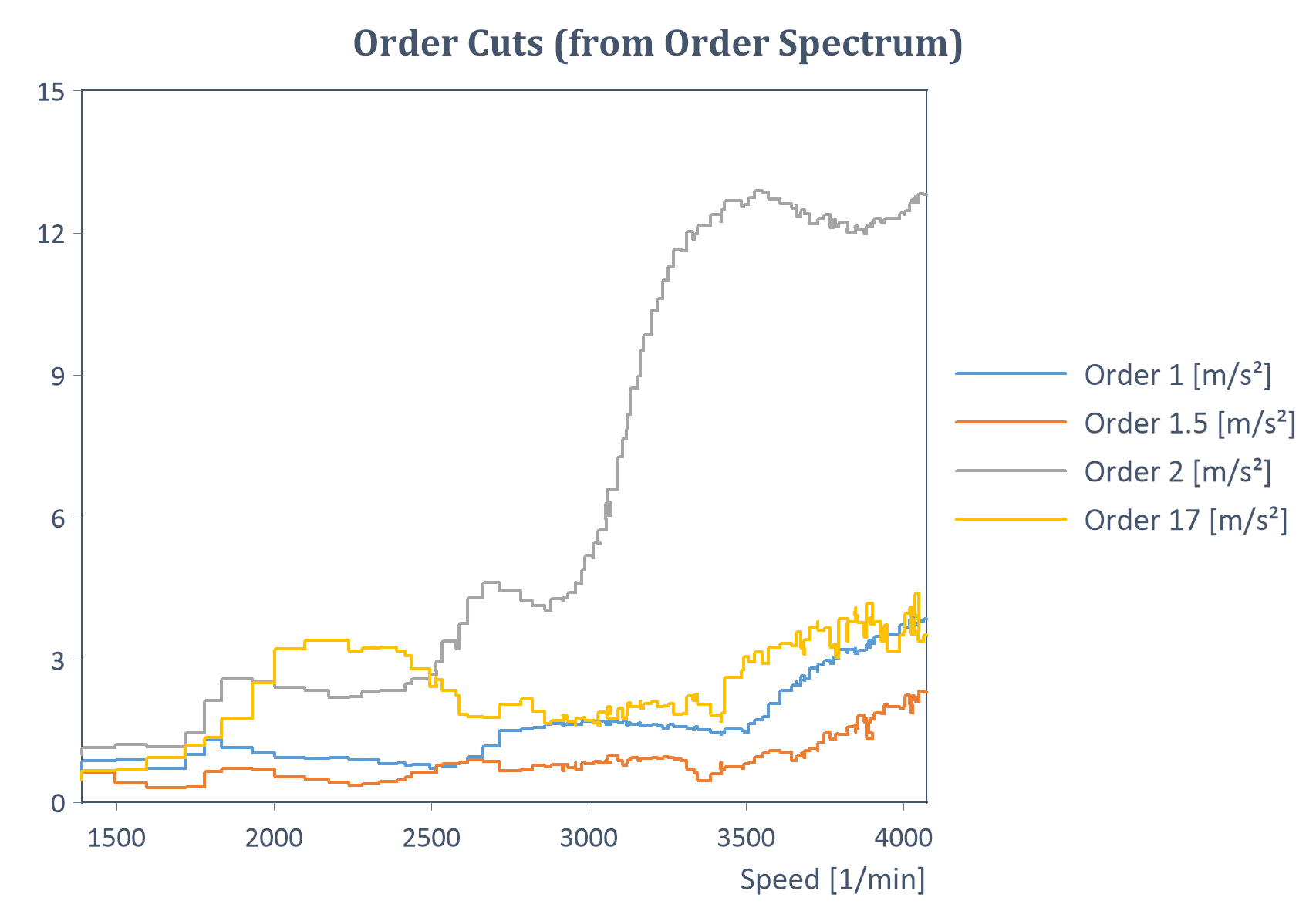
Ergebnis der gemittelten RMS-Ordnungsanalyse

Bei Wahl des Ausgabemodus Gemittelte RMS-Ordnungsanalyse, sind die folgenden Ergebnistypen auswählbar.

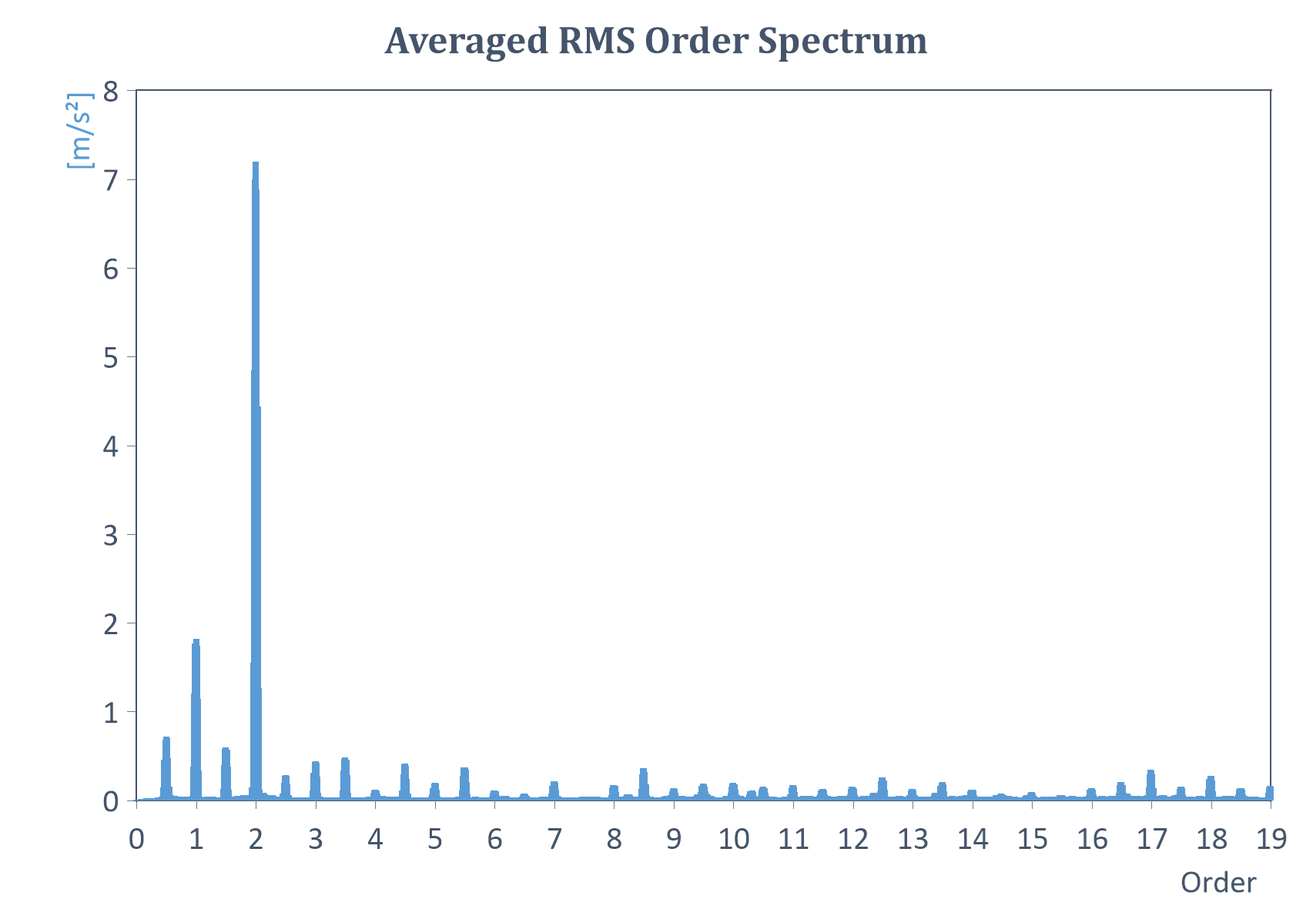
Beispiel eines gemittelten RMS-Ordnungsspektrums einer Ordnungsanalyse mit konstanter Drehzahl:

Beispiele

In der Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Order Tracking Analysis.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021\Examples\Order Tracking Analysis.fpd finden Sie Beispiele für die verschiedenen Anwendungsfälle und Modi, für die eine Ordnungsanalyse durchgeführt werden kann. Obige Diagramme sind dort insbesondere enthalten.

Verwendete FPScript-Funktion

RevolutionSyncSampling

OrderCuts

STFTSpectrum

ImpulseToFrequency

DCRemovalFilter

Siehe auch

Analyseobjekte

Option Ordnungsanalyse

Analyseobjekt Ordnungsfilter

Analyseobjekt Umdrehungssynchrone Abtastung

Zeit-Frequenz Spektralanalyse

Fourier-Spektralanalyse

Oberwellenfilter