Das Analyseobjekt Ordnungsfilter berechnet eine Ordnungsanalyse für drehzahlabhängige Schwingungen durch Bandpassfilterung einzelner Ordnungen. An rotierenden Maschinen gemessene Vibrationen zeigen ein Spektrum, in dem Maxima bei Frequenzen auftreten, die einem Vielfachen der Drehzahl der Maschine entsprechen. Für das Auftreten dieser Maxima gibt es zwei verschiedene Ursachen. Einerseits kann man die Maschine als nicht-lineares Übertragungssystem betrachten, welches mit einer der Drehzahl entsprechenden, harmonischen Schwingung angeregt wird. Die Nicht-Linearität erzeugt Oberwellen dieser Grundschwingung, welche zu entsprechenden Maxima führen. Andererseits kann eine solche Maschine Komponenten enthalten, deren Drehzahl nicht gleich der Grunddrehzahl ist, aber immer einem festen Vielfachen dieser Drehzahl entspricht. So haben z. B. verschiedene Wellen in einem Getriebe unterschiedliche Drehzahlen. Aber auch die Zähne eines Zahnrades oder die Kugeln in einem Kugellager erzeugen Vibrationen, die in fester Relation zur Drehzahl stehen. Kennt man dieses als Ordnung bezeichnete Verhältnis aus Grundfrequenz einer Komponente zur Grundfrequenz der Maschine, dann lassen sich einzelne Maxima im Spektrum gezielt einer einzigen oder wenigen Komponenten der Maschine zuordnen. Hiermit kann z. B. die Ursache von Resonanzen isoliert werden.

Bei dem hier eingesetzten Verfahren wird zunächst eine Abtastratenumwandlung des Zeitsignals durchgeführt (umdrehungssynchrone Umabtastung), so dass das Signal nicht mehr in zeitlich äquidistanten Schritten, sondern in äquidistanten Drehwinkelschritten (d.h. äquidistanten Umdrehungsintervallen) vorliegt. Dies erlaubt auf effektive Weise die Durchführung einer Ordnungsanalyse, da eine gewöhnliche Bandpassfilterung des in den Umdrehungsbereich konvertierten Signals (z.B. mit Hilfe eines geeigneten IIR-Bandpassfilters um die jeweilige Ordnung) dann unmittelbar die einzelnen Ordnungsverläufe liefert (Details siehe RevolutionSyncSampling):

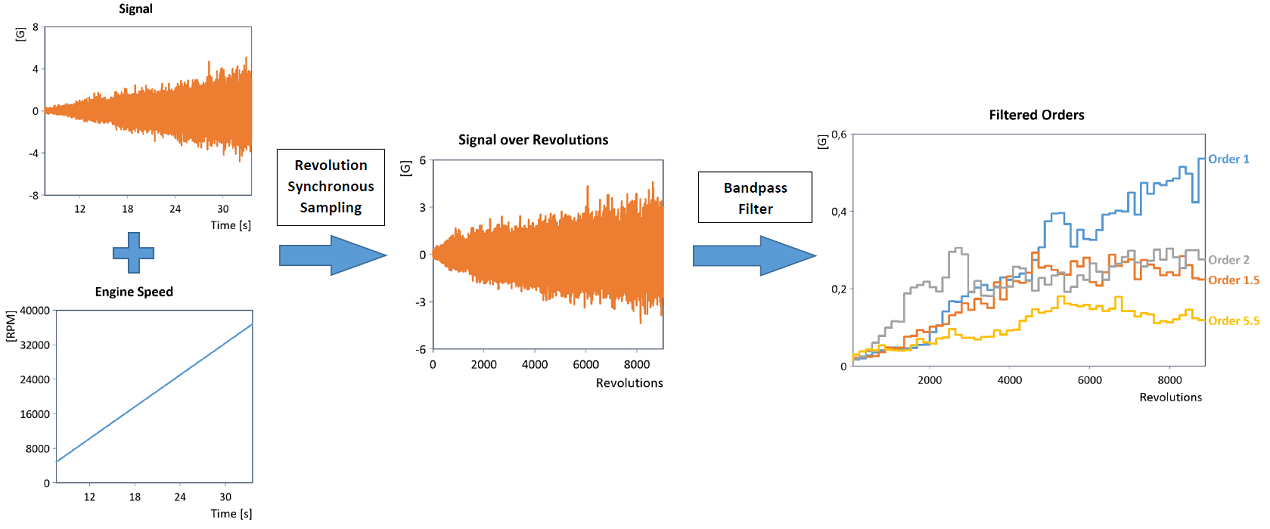
Das Analyseobjekt Ordnungsfilter erlaubt (im Gegensatz zum Analyseobjekt Umdrehungssynchrone Ordnungsanalyse) die Berechnung und Rückgabe der gefilterten Ordnungen im ursprünglichen Zeitbereich. Das Analyseobjekt lässt sich daher ebenso für akustische Analysen der gefilterten Ordnungen einsetzen.

Zur Ordnungsanalyse werden vorwiegend zwei Messverfahren angewendet. Bei einem Hochlauf, werden die Vibration und die Momentandrehzahl synchron gemessen, während die Maschine gewöhnlich langsam von ihrer Mindest- zu ihrer Maximaldrehzahl hochgefahren wird (Hochlaufanalyse). Bei einem zweiten Verfahren wird die Maschine zunächst auf eine bestimmte Drehzahl gebracht und dann wird für diese Drehzahl eine Messung der Vibration durchgeführt (Ordnungsanalyse mit konstanter Drehzahl). Das Analyseobjekt Ordnungsfilter unterstützt beide Varianten. Zudem ist die Ordnungsanalyse durch Ordnungsfilterung mittels umdrehungssynchroner Umabtastung äußerst flexibel und lässt sich sogar für verrauschte sowie nicht-monotone Drehzahldatensätze durchführen (Ordnungsanalyse mit variabler Drehzahl).

Registerkarte Daten

Diese Registerkarte spezifiziert die Eingangsdaten und die Parameter zur Transformation vom Zeit- in den Umdrehungsbereich (Details siehe auch RevolutionSyncSampling):.

Signale im Zeitbereich

Das für das Analyseobjekt zu analysierende Zeitsignal muss in der Datenstruktur Signal vorliegen. Die Drehzahl kann entweder in der Datenstruktur Signal (entspricht einer Hochlaufanalyse oder einer Ordnungsanalyse mit variabler Drehzahl) oder als Einzelwert (entspricht Ordnungsanalyse mit konstanter Drehzahl oder zu fester Grundfrequenz) angegeben werden.

Bei fehlenden Einheiten oder ausgeschalteter Einheitenverwaltung, wird die Drehzahl stets in der Einheit [1/min] und die X-Komponente des Zeitsignals in der Einheit interpretiert.

Die Momentandrehzahl wird oft mit einem Impulsgeber gemessen, der eine bestimmte Anzahl von Impulsen pro Umdrehung erfasst. Sie können das hieraus resultierende Impulssignal direkt in ein Drehzahlsignal konvertieren. Markieren Sie hierzu die Option Drehzahl ist Impulssignal und geben Sie die Anzahl der Impulse pro Umdrehung an. Die Konvertierung des Impulssignals in ein Drehzahlsignal erfolgt mit der ImpulseToFrequency-Funktion.

Umabtastung in den Umdrehungsbereich

Zur Umabtastung vom Zeit- in den Umdrehungsbereich stehen drei verschiedene Modi zur Verfügung. In den meisten praktischen Anwendungsfällen ist die lineare Umabtastung ausreichend:

Bei Wahl des Splines- oder des FFT-Resampling-Verfahrens, muss ein Resample-Faktor spezifiziert werden, um den die Abtastrate des Signals beim Transformationsalgorithmus erhöht wird.

Unabhängig vom gewählten Resample-Verfahren, sind die Anzahl der Datenpunkte pro Umdrehung für das in den Umdrehungsbereich zu transformierenden Signals anzugeben. Dies bestimmt die Abtastung des transformierten Signals im Umdrehungsbereich. Gemäß Nyquist-Abtasttheorem bestimmt die Hälfte dieses Wertes die maximale Ordnung, die überhaupt berechnet werden kann.

Zur Bestimmung der Anzahl der Datenpunkte pro Umdrehung stehen zwei Modi zur Verfügung:

Registerkarte Optionen

In dieser Registerkarte wird das Ordnungsfilter zur Bandpassfilterung einzelner oder mehrere Ordnungen spezifiziert. Hierbei wird eine gewöhnliche IIR-Bandpassfilterung um die jeweilige Ordnung des in den Umdrehungsbereichs transformierten Signals durchgeführt (Details siehe auch RevolutionSyncSampling).

Ausgabe

Es stehen die folgenden vier Ausgabemodi des Analyseobjekts Ordnungsfilter zur Verfügung:

Bandpass-Filter

Zur Berechnung der Ordnungsverläufe wird eine gewöhnliche IIR-Bandpassfilterung um die jeweilige Ordnung des in den Umdrehungsbereichs transformierten Signals durchgeführt. Die folgenden Bandpass-Filter stehen zur Verfügung:

Zu filternde Ordnungen

Die zu filternden Ordnungen können in einer Tabelle explizit eingestellt oder aus einem Datensatz entnommen werden. Die ausgewählten Ordnungen bilden die Bandmittenfrequenz des eingestellten Bandpass-Filter. Ordnungsbandbreiten lassen sich symmetrisch um die Ordnung als 3dB-Filterbandbreiten spezifizieren. Die 3dB-Filterbandbreite definiert hierbei den Ordnungsbereich, außerhalb dessen Ordnungen ausgesperrt werden (festgelegt durch -3 dB Punkt, d.h. Stelle bei der 70,7 Prozent der ursprünglichen Signalamplitude erreicht wird).

RMS-Berechnung

Zur Berechnung der RMS-Verläufe der gefilterten Ordnungen (als Liste oder Signalreihe) oder zur RMS-Berechnung der Summe der gefilterten Ordnungen, stehen die folgenden beiden RMS-Modi zur Auswahl:

Beispiel eines Ordnungsfilter mit blockweiser RMS-Berechnung für einen Hochlauf (mit Y = Amplitude, X = Drehzahl):

Ergebnis

Es stehen für alle Ausgabemodi (mit Ausnahme der gemittelten RMS-Ordnungsanalyse) die folgenden Ergebnistypen zur Verfügung:

Bei Ergebnis Y = Amplitude, X = Drehzahl, enthält das Ergebnis nicht-äquidistante Drehzahlstützpunkte (diese entsprechen exakt den äquidistanten Umdrehungsstützpunkten nach Filterung im Umdrehungsbereich). Das Ergebnis kann daher zusätzlich über einem äquidistanten Drehzahlbereich mit festzulegender Startdrehzahl, Enddrehzahl und Drehzahlschrittweite ausgewertet werden. Hierbei erfolgt eine lineare Interpolation über dem angegebenen äquidistanten Drehzahlbereich. Damit die lineare Umabtastung sinnvolle Resultate ergibt, sollte die vom Algorithmus berechnete Drehzahlauflösung ausreichend hoch sein (z.B. gleitende RMS-Berechnung oder blockweise RMS-Berechnung mit ausreichend kleiner Blockgröße).

Bemerkung: Die Berechnung der (blockweisen) RMS-Verläufe der zu filternden Ordnungen liefert Verläufe ähnlich zum Analyseobjekt Umdrehungssynchrone Ordnungsanalyse. Hierzu muss im letztgenannten Analyseobjekt der Ausgabemodus Ordnungsschnitte inklusive RMS-Pegel Extraktion im Ordnungsband eingestellt werden. Die gemittelte RMS-Ordnungsanalyse beider Analyseobjekte liefert ebenso gleiche Resultate.

Beispiel eines Ordnungsfilter über der Zeit für einen Hochlauf (Y = Amplitude, X = Zeit):

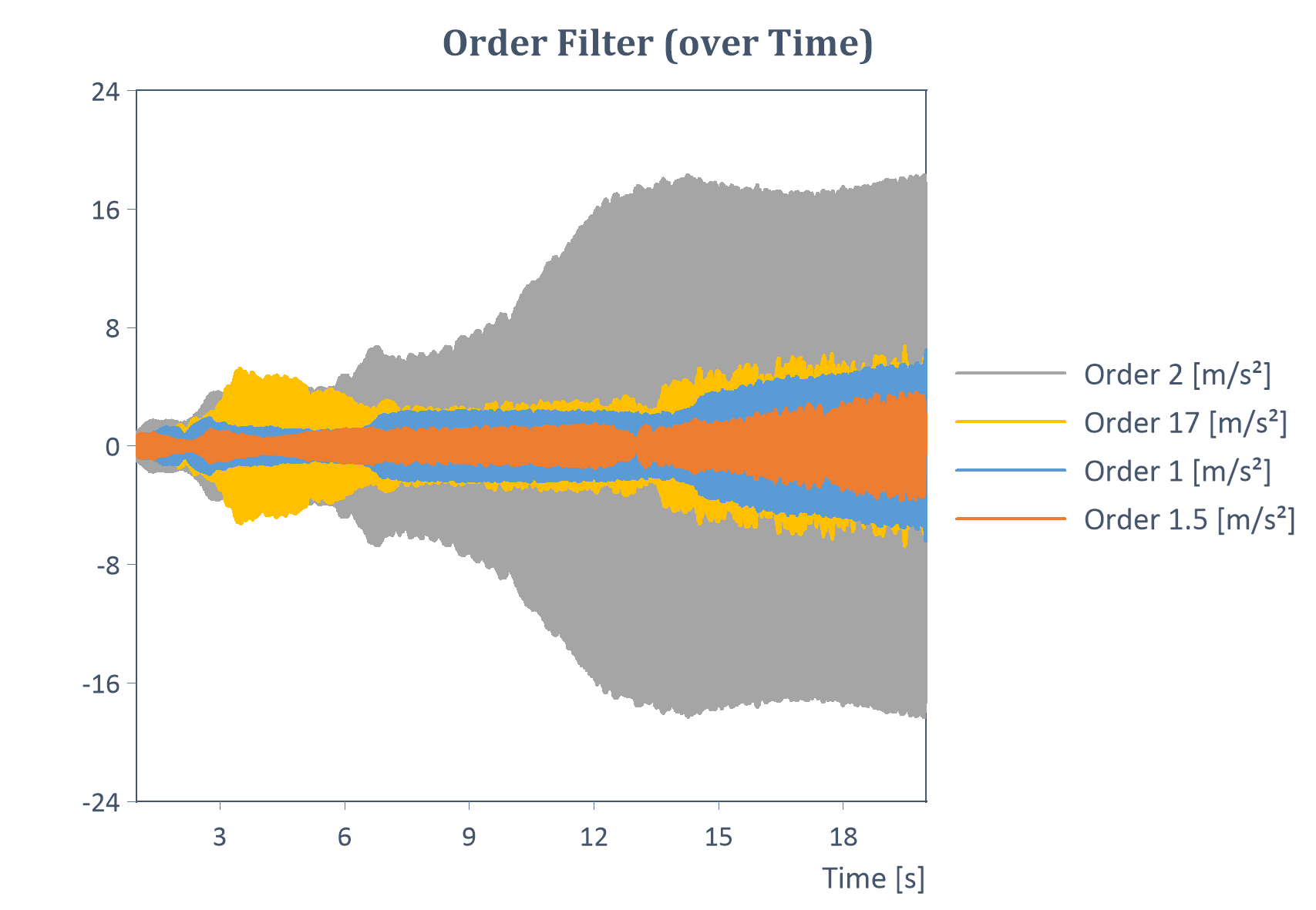
Beispiel einer gemittelten RMS-Ordnungsanalyse für ein Signal mit konstanter Drehzahl (RMS jeder gefilterten Ordnung):

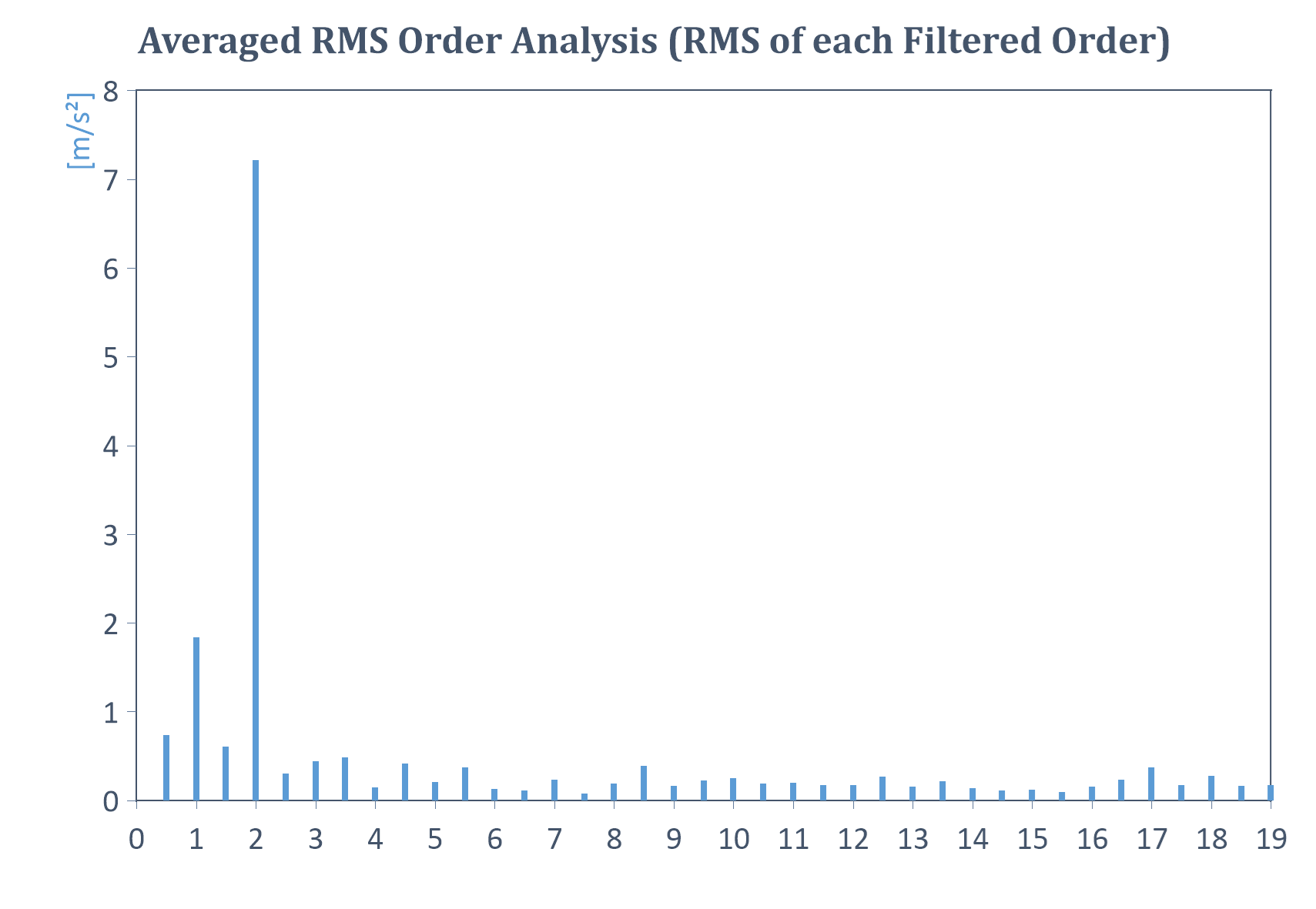
Beispiele

In der Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Order Tracking Analysis.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021\Examples\Order Tracking Analysis.fpd finden Sie Beispiele für die verschiedenen Anwendungsfälle und Modi, für die eine Ordnungsanalyse durchgeführt werden kann. Obige Diagramme sind dort insbesondere enthalten.

Verwendete FPScript-Funktion

RevolutionSyncSampling

IIRFilter

IIRPeakFilter

ImpulseToFrequency

Siehe auch

Analyseobjekte

Option Ordnungsanalyse

Analyseobjekt Umdrehungssynchrone Ordnungsanalyse

Analyseobjekt Umdrehungssynchrone Abtastung

IIR-Filter

Oberwellenfilter