Fourier Zerlegung

Die Schnelle Fourier-Transformation (FFT = Fast Fourier Transform) zerlegt ein Zeitsignal (welches auch Funktion einer beliebigen anderen Variable sein kann) in komplexe Exponentialfunktionen (Sinus und Kosinus). Eine Fourier-Transformation bietet eine vollständige Information über den Frequenzraum, enthält aber keinerlei Information über das zeitliche Auftreten von Signalkomponenten. Deshalb muss das Signal entweder weit reichend stationär sein, mit konstantem Mittelwert und Varianz über weite Zeitbereiche, oder es sind nur qualitative Aussagen über spektrale Komponenten möglich, wenn diese irgendwo in dem erfassten Zeitbereich auftreten.

Die FFT ist ein schneller Algorithmus zur Erzeugung einer Diskreten Fourier-Transformation (DFT). Die DFT und ihre Rücktransformation sind wie folgt definiert:

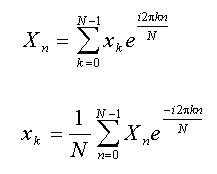
Die DFT ist zwar sehr einfach, hat jedoch eine Laufzeit, die proportional zu n² ist. Die FFT ist dagegen proportional zu n*log2(n). Der Unterschied in der Berechnungsgeschwindigkeit ist für große Datensätze dramatisch. Die in FlexPro verwendete "best-exact-n" FFT verwendet vier verschiedene FFT-Algorithmen.

Die Fourier-Zerlegung ist in ihrer Auflösung beschränkt, da die Frequenzen, für die die Sinus- und Kosinusfunktionen berechnet werden, gleich verteilt und in Ihrer Anzahl festgelegt sind. Für einen Datensatz mit n Werten erhält man n komplexe Frequenzen. Bei reellen Eingangsdaten spiegeln die negativen Frequenzen die positiven und es werden deshalb nur die positiven dargestellt. Hieraus ergibt sich dann eine Anzahl von n / 2 + 1 Frequenzen im Spektrum. Normierte Frequenzen liegen im Bereich von 0 bis 0,5, der Nyquist-Frequenz. Die Frequenz 0 entspricht dem Gleichanteil oder Mittelwert des Zeitsignals und wird oft als DC bezeichnet. Die Nyquist-Frequenz ist die höchste Frequenz, die bei einer gegeben Abtastrate noch erkannt werden kann. Für Signalanteile dieser Frequenz existieren noch zwei Abtastwerte pro Periode im Zeitsignal. FlexPro stellt in der Regel die tatsächlichen Frequenzen dar. Normierte Frequenzen werden nur dann verwendet, wenn keine Zeitinformation im Eingangsdatensatz vorhanden ist.

Stetige Elementarfunktionen

Die Fourier-Zerlegung stellt die Eingangsdaten als Linearkombination von Sinus- und Kosinus-Elementarfunktionen dar. Obwohl die Daten als auch die daraus resultierende Fourier-Reihe diskret sind, sind die Elementarfunktionen kontinuierlich und unbeschränkt in ihrer zeitlichen Ausdehnung. Es ist deshalb möglich, das Zeitsignal für einen beliebigen Zeitpunkt im Bereich der ursprünglichen Sequenz zu berechnen:

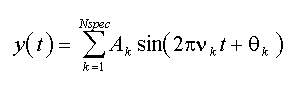
Die Fourier-Elementarfunktionen können als komplexe Exponentialfunktionen, als Paare von Sinus- und Kosinusfunktionen ohne Phase oder als Sinusfunktionen mit Phase bzw. Kosinusfunktionen mit Phase dargestellt werden. In FlexPro werden von allen Fourier-basierten Algorithmen die Phasen der Kosinus-Elementarfunktionen im Bereich von -π/2 bis +π/2 ausgegeben. In der obigen Gleichung ist A die ausgegeben Amplitude, ν ist die Frequenz und θ ist die Phase. Das Signal kann zu einem beliebigen Zeitpunkt t rekonstruiert werden, in dem die Werte aller Nspec Kosinusfunktionen im Spektrum für diesen Zeitpunkt ausgewertet und aufsummiert werden. Die Amplituden sind so angepasst, dass die gesamte Signalleistung von den positiven Frequenzen repräsentiert wird.

Leckeffekt

Der Begriff Leckeffekt (spectral leakage) bezeichnet den Verlust an Leistung einer bestimmten Frequenz an andere Frequenzlinien im Spektrum. Die Approximation eines endlich langen Datensatzes durch eine unendliche Fourier-Reihe geht davon aus, dass die Daten vollständig periodisch sind. Das berechnete Spektrum ist das eines Datensatzes, der sich durch unendliches Aneinanderhängen des vorhandenen Datensatzes ergibt. Leider können nur die wenigsten Datensätze aneinander gehängt werden, ohne dass an den Rändern eine Unstetigkeit entsteht. Diese Unstetigkeiten sind eine Ursache für den Leckeffekt.

Der Leckeffekt tritt auch wegen der festen und linear verteilten Anzahl von Frequenzlinien, die bei der FFT vorhanden ist, auf. Wenn die Frequenz einer Elementarfunktion nicht genau auf eine Spektrallinie fällt, wird ein Teil der Signalleistung in andere Spektrallinien "lecken". Man kann daher davon ausgehen, dass ein Teil der benachbarten Spektralwerte zu diesem Peak beitragen. Es kann sogar der Fall sein, dass wenn die Frequenz einer Spektralkomponente nicht mit einer Frequenzlinie zusammenfällt, alle Spektrallinien im Spektrum einen Teil der von dieser Komponente herrührenden Varianz tragen. Dieser Effekt nimmt ab, je weiter man sich von der interessierenden Frequenz wegbewegt.

Mann kann eine FFT auch als lineare Approximation eines Modells von gleichverteilten Sinus- und Kosinusfunktionen ansehen. Wenn eine einzelne Sinusfunktion nicht-linear approximiert wird, können die Parameter vollständig ermittelt werden, da Amplitude, Frequenz und Phase frei variieren können. Dies ist bei einer FFT nicht möglich. Während die Amplitude und Phase variieren können, kann die Frequenz dies nicht. Wenn eine Sinusfunktion nicht genau auf eine der vorgegeben Frequenzen fällt, wird diese über mehrere Frequenzen verschmieren.

Während der aus der festen Anordnung der Frequenzen resultierende Leckeffekt ein inhärentes Problem der FFT ist, kann viel zur Eliminierung der aus den Randeffekten resultierenden Leckage getan werden. Um den Leckeffekt zu minimieren, kann ein Datensatz verwendet werden, der eine unendliche stetige Reihe dadurch approximiert, dass er an beiden Rändern auf Null gedämpft wird. Dies wird durch Bewertungsfenster erreicht.

Bewertungsfenster

Diese Fenster werden generell im Zeitbereich angewandt, auch wenn diese im Frequenzbereich konstruiert werden. Dies ist deshalb der Fall, weil im Zeitbereich eine einfache Multiplikation genügt um die Bewertung vorzunehmen. FlexPro bietet eine breite Palette von Bewertungsfenstern an, die bei der Signalverarbeitung geläufig sind.

Ein Rechteck-Fenster (es wird keine Bewertung vorgenommen) erzeugt eine einseitige spektrale Breite von 1,0 im Frequenzbereich. Die Bewertungsfenster von FlexPro variieren in ihrer spektralen Breite im Bereich von 1,1 bis 6,0. Viele gebräuchliche Fenster haben Breiten von 2,0, 3,0 und 4,0. Wenn ein Datensatz fensterbewertet wird, werden Teile des Signals an den Rändern unterdrückt und die Auflösung wird vermindert. Ein Fenster der Breite 2 vermindert die Auflösung um die Hälfte und ein Fenster der Breite 4 auf ein Viertel.

Obwohl ein Teil der Daten unterdrückt wird und trotz dem Verlust an Auflösung ist eine fensterbewertete FFT oft der beste Weg, um spektrale Komponenten genau abzuschätzen. Dadurch, dass die Daten an den Rändern gleichmäßig auf Null gedämpft werden, wird der Leckeffekt in einem Maße verringert, dass dieser nur noch in einer logarithmischen Skalierung erkennbar wird.

Wenn die FFT Daten verarbeitet werden, die mit einem Fenster bewertet wurden, dann vergrößert sich effektiv die Breite der Frequenzlinien (frequency bins). Diese Breite wird oftmals auch als die Ordnung des Fensters bezeichnet. Die Fenster Hann und Hamming streuen die Spektralinformation auf zwei Spektrallinien und sind deshalb Fenster der Ordnung 2. Durch diese Steuerung vermindert sich der Leckeffekt, der auftritt, wenn eine spektrale Komponente zu Nahe am Rand eines Frequenz-Bin liegt. Unter der Vielzahl von Eigenschaften, die ein Bewertungsfenster hat, ist die Breite die wichtigste, da diese sowohl die spektrale Auflösung bestimmt, als auch den maximalen Dynamikbereich der FFT. Jedes Fenster hat charakteristische Eigenschaften und ist für einen speziellen Zweck optimiert. Einige Fenster haben einen einstellbaren Parameter, der für alle Bewertungsfenster von FlexPro so ausgelegt ist, dass er die Breite des Hauptmaximums (main lobe) steuert.

Einige Fenster minimieren den Leckeffekt als Ganzes mit dem Nachteil, dass dieser mit der Entfernung von der betrachteten Frequenzlinie nicht mehr abklingt (rolloff). Diese Fenster bieten eine hervorragende Auflösung für dicht beieinander liegende Peaks unterschiedlicher Höhe aber können weit entfernt liegende Peaks mit viel niedrigerer Leistung überdecken. Das Tschebyscheff-Fenster weist den minimalen Leckeffekt für benachbarte Frequenzlinien bei gegebener Fensterbreite auf. Andere Fenster optimieren das Abklingen (rolloff) des Leckeffekts auf Kosten von dessen Betrag für die benachbarten Frequenzlinien. Zwei weit entfernte Peaks mit niedriger Leistung werden zwar gut dargestellt, aber ein Peak mit geringerer Leistung, der dicht neben einem mit hoher Leistung liegt kann komplett überdeckt werden.

Es gibt also zwei Kriterien bei der Wahl eines Bewertungsfensters. Das erste ist die Auflösung. Wählen Sie die größtmögliche Fensterbreite so, dass die Auflösung akzeptabel bleibt. Das zweite Kriterium ist die Verteilung der aufzulösenden Peaks. Wenn Sie vorwiegend weit verteilte Peaks mit niedriger Leistung erkennen möchten, wählen Sie ein Maximum-Rolloff-Fenster, d. h. ein Fenster, bei dem die Seitenmaxima schnellstmöglich abklingen. Wenn Sie eng benachbarte Peaks unterschiedlicher Leistung auswerten möchten, wählen Sie ein Minimum-Sidelobe-Fenster, d. h. ein Fenster mit maximaler Dämpfung des ersten Nebenmaximums. Oft eignet sich ein Kompromiss. Die besten bekannten Fenster, wie z. B. das beliebte Cos4 Blackman-Harris Fenster tendieren dazu, die Dämpfung des ersten Nebenmaximums zu optimieren.

Eine Besonderheit stellt das Flattop-Fenster dar. Dieses weist zwar eine Breite des Hauptmaximums von 5 auf, bietet also eine relativ geringe spektrale Auflösung, dafür hat das Hauptmaximum jedoch im vollen Bereich von einer Frequenzlinie bis zu deren linken und rechten Nachbar nahezu den gleichen Betrag. Das Hauptmaximum weist also eine zwar breite aber dafür flache Spitze auf. Dieses Fenster eignet sich damit insbesondere zum Ausmessen der Leistungen bzw. Amplituden schmalbandiger Signalkomponenten, d. h. einzelner Peaks im Spektrum. Die Höhe eines Peaks wird nämlich durch die spezielle Form des Hauptmaximums nahezu unabhängig von dessen Lage zwischen zwei Frequenzlinien.

Periodogramm-Mittelung

Die Bewertungsfenster unterdrücken Information am Rand des Fensters und heben den Spektralgehalt in der Mitte des Datensatzes hervor. Wenn die Daten stationär sind, dann resultiert hieraus lediglich eine erhöhte Varianz der Spektralschätzung. Das Periodogramm ist eine Spektralprozedur, die dieses Problem behebt. Bei diesem Verfahren werden für überlappende Datensegmente fensterbewertete FFTs berechnet und dann gemittelt. Hierdurch wird die Varianz auf Kosten der spektralen Auflösung vermindert.

Multitaper-Analyse

Ein weiterer Algorithmus, der die Information am Rand des Datensatzes einbezieht, ist das Multitaper-Spektrum. Bei diesem Verfahren werden die Spektren einer Sequenz von orthogonalen Fenstern gemittelt. Das Ergebnisspektrum hat ebenfalls eine reduzierte Varianz, es sind sämtliche Daten berücksichtigt und die spektrale Auflösung entspricht in etwa einer einfachen fensterbewerteten FFT.

Literatur

Gute Einführungen in die digitale Signalverarbeitung sind:

•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.

•H.D. Lüke (1985). Signalübertragung. Springer-Verlag Berlin, Heidelberg, New York. ISBN 3-540-15526-0.

Die in FlexPro verwendeten FFT-Algorithmen sind beschrieben in:

•C. Temperton, "Implementation of a Self-Sorting In-Place Prime Factor FFT Algorithm", Journal of Computational Physics, v. 58, p. 283, 1985

•R. C. Singleton, "An Algorithm for Computing the Mixed Radix Fast Fourier Transform", IEEE Trans. Audio Electroacoust., v. AU-17, p. 93, June 1969

•L. R. Rabiner, R. W. Schafer, C. M. Rader, "The Chirp z-Transform Algorithm and Its Application", BSTJ, 48, p.1249, May-June 1969

Information über Bewertungsfenster finden Sie in:

•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, Feb. 1981.

Information über Multitaper-Spektren bietet:

•Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis", Computers and Geosciences, v21, p199, 1995.