weisang.com > Dokumentation > Analyseobjekt Momentangröße (Option Spektralanalyse)

FlexPro-Dokumentation

Analyseobjekt Momentangröße (Option Spektralanalyse)

09.03.2021

Mit diesem Analyseobjekt können Sie Momentangrößen (Momentanamplitude, Momentanphase und Momentanfrequenz) von Signalen bestimmen. Die Momentanamplitude liefert den Amplitudenverlauf, die Momentanphase den Phasen- und die Momentanfrequenz den Frequenzverlauf des zu analysierenden Signals. Falls das zugrundeliegende Signal keinen Trend besitzt, so stimmt die Momentanamplitude ebenso mit der oberen Einhüllenden des Signals überein.

Die Berechnung der Momentangrößen ist nur für einkomponentige Signale geeignet.

Im folgenden Beispiel wird beispielsweise die Momentanamplitude sowie Momentanfrequenz eines amplitudenmodulierten Wobbelkosinus mit Hilfe des Analyseobjekts Momentangröße bestimmt:

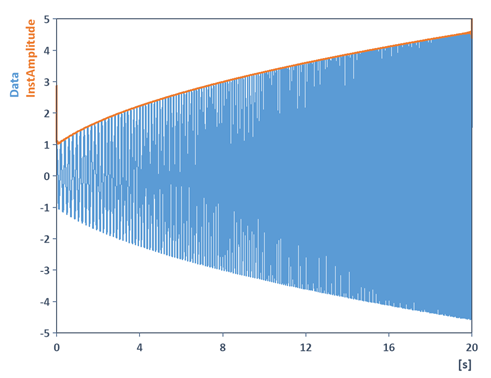
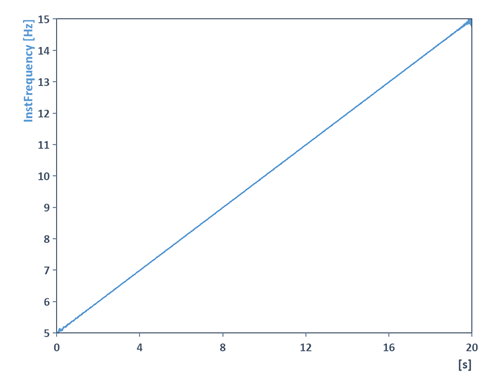
Die Momentangrößen können damit ebenso zur Demodulation von Signalen (Amplitudendemodulation, Phasendemodulation, Frequenzdemodulation) verwendet werden. Details finden Sie in der Online-Hilfe zur AnalyticSignal-Funktion.

Algorithmus

In der englischen Literatur werden diese Momentangrößen gewöhnlich als Instantaneous Amplitude (oder Instantaneous Envelope), Instantaneous Phase sowie Instantaneous Frequency bezeichnet und mit der Hilbert-Transformation berechnet. Details finden Sie in der Online-Hilfe zur Hilbert-Funktion oder zur AnalyticSignal-Funktion.

Parameter: FFT-Länge

Die Hilbert-Transformation führt intern eine Fourier-Transformation (FFT) des Datensatzes durch. Mittels Zero-Padding, d.h. durch Wahl der FFT-Länge größer als die Datenlänge, wird die Auflösung der für den Algorithmus benötigten FFT erhöht. Das Berechnungsresultat kann dadurch verbessert werden. Im Analyseobjekt lassen sich die folgenden Einstellungen für die FFT-Länge auswählen:

Auswahl	Bedeutung
Datenlänge	Setzt die FFT-Länge auf die Datenlänge.
Nächste 2er-Potenz	Setzt die FFT-Länge auf die nächst größere 2er-Potenz.

Parameter: Trend entfernen

Für Signale, die einen Trend bzw. Offset besitzen, muss zur Bestimmung der Momentangrößen der Trend zuvor entfernt werden. Die nachfolgend aufgeführten Auswahlmöglichkeiten stehen im Analyseobjekt zur Verfügung. Die Auswahlmöglichkeiten stimmen dabei mit den Auswahlmöglichkeiten zur Trendentfernung des Analyseobjekt Signalanalyse überein:

Auswahl	Bedeutung
Konstant	Subtrahiert den Mittelwert des Datensatzes.
Linear	Subtrahiert die Bestgerade, d. h. die Gerade für die die Summe der Quadrate der Abweichungen zum Datensatz minimal ist.
Adaptiv	Subtrahiert den Mittelwert aus oberer und unterer Hüllkurve. Die Einstellung kann verwendet werden, wenn der vorliegende Trend weder konstant noch linear ist, sondern zeitabhängig ist.
gleitender Mittelwert	Subtrahiert den gleitenden Mittelwert. Die zur Bildung des gleitenden Mittelwerts benötigte Intervallbreite kann eingegeben werden. Die Einstellung kann verwendet werden, wenn der vorliegende Trend weder konstant noch linear ist, sondern zeitabhängig ist. Der gleitende Mittelwertfilter ist ein Hochpassfilter.
DC-Offset Filter	Hochpassfilter zum Entfernen des DC-Offsets (IIR-Butterworth-Hochpass). Die Grenzfrequenz sowie die Ordnung (d.h. Steilheit) des Hochpassfilters kann eingestellt werden. Das Filter kann verwendet werden, wenn der vorliegende Trend weder konstant noch linear ist, sondern zeitabhängig ist.

Bei der Ermittlung des konstanten bzw. linearen Trends wird zunächst der Mittelwert des Signals berechnet und dann der erste und letzte Pegeldurchgang durch diesen Wert gesucht. Wenn zwei Pegeldurchgänge gefunden wurden, dann wird der Mittelwert bzw. die Bestgerade nur für den Bereich zwischen diesen beiden Pegeldurchgängen berechnet. Dies verhindert Fehler, die durch den Phasenanschnitt periodischer Signale an den Enden des Datensatzes auftreten. Wenn keine Pegeldurchgänge gefunden wurden, dann werden alle Werte in die Berechnung einbezogen. Passende Einstellungen zum Entfernen eines zeitabhängigen Trends sind gewöhnlich die Subtraktion des gleitenden Mittelwerts sowie der DC-Offset Filter.