Berechnung des analytischen Signals
Definition Momentanamplitude, Momentanphase und Momentanfrequenz
Durch Transformation des reellen Eingangssignal in ein analytisches Signal lassen sich lokale Kenngrößen des Originalsignals, die Momentanamplitude, Momentanphase und Momentanfrequenz, ableiten und betrachten:
Dazu schreibe man das analytische Signal z(t) in Polardarstellung wie folgt:
Die Momentanamplitude (in englischer Literatur Instantaneous Amplitude oder Instantaneous Envelope) ist nun definiert als die Amplitude a(t) des analytischen Signals, d.h.:
Wenn das Originalsignal keinen Trend bzw. Offset besitzt, so liefert dies tatsächlich den Amplitudenverlauf bzw. die obere Einhüllende des zu analysierenden Signals.
Als Momentanphase (in englischer Literatur Instantaneous Phase) bezeichnet man nun die Phase des analytischen Signals Φ(t). Die Phase Φ(t) kann in folgender Form modelliert werden:
Die Momentanfrequenz ω(t) (in englischer Literatur Instantaneous Frequency) ist damit schließlich definiert als:
Für einkomponentige Signale ohne Trend bzw. Offset, liefern diese Definitionen den Phasenverlauf sowie Frequenzverlauf des zu analysierenden Signals.
Für Signale, die einen Trend bzw. Offset besitzen, sind alle oben genannten Interpretationen nur korrekt, wenn eine Trendkorrektur des Signals erfolgt. Nachfolgendes Beispiel verdeutlicht diese Zusammenhänge.
Für weitere Details siehe auch [2] und [3].
Anwendungen: Berechnung Momentanamplitude, Momentanphase, Momentanfrequenz und Einhüllende
Vorbemerkung: Die nachfolgend aufgeführten FPScript-Formeln zur Berechnung der Momentanamplitude, Momentanphase und Momentanfrequenz bilden die Grundlage des Analyseobjekts Momentangröße. Das folgende Beispiel kann somit mit dem Analyseobjekts Momentangröße in analoger Form durchgerechnet werden.
Für das Demo-Beispiel erzeugen Sie zuerst einen Wobbelkosinus mit 10000 Werten, dessen X-Komponente die Einheit s besitzt, bei 0 s startet und bei 20 s endet. Die Startfrequenz sei 5 Hz, die Endfrequenz sei 15 Hz. Die Amplitude des Wobbelkosinus sei 1, der Offset und die Startphase jeweils 0. Skalieren Sie nun das erzeugte synthetische Signal mit Hilfe der folgenden Formel (namens Data):
Dim amplitude = Sqrt(Value Signal.X + 1)
amplitude * Signal
Das Zeit-Frequenz-Spektrum des skalierten Signals liefert (visualisiert in einem 3D-Konturdiagramm):
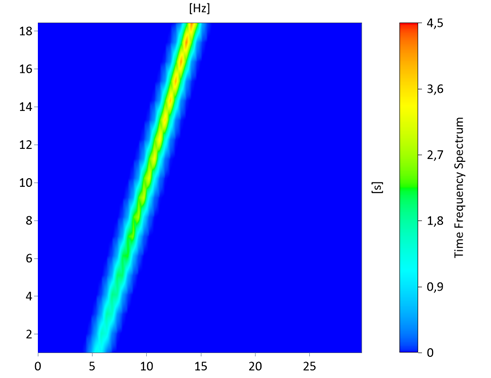
Das Signal besitzt keinen Trend. Die Momentanamplitude berechnet sich daher nun wie folgt in der Form:
Absolute(AnalyticSignal(Data))
Dies entspricht nun, wie oben angemerkt, der oberen Einhüllenden (bzw. des Amplitudenverlaufs) des skalierten Signals:
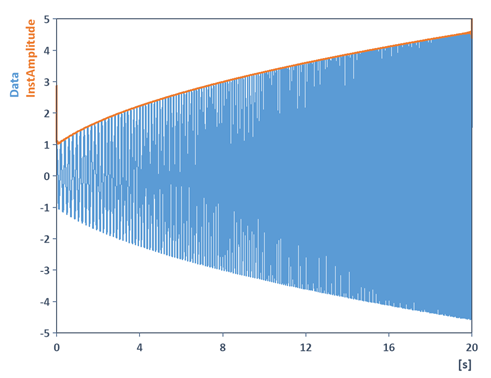
Die untere Einhüllende erhalten Sie analog mittels
-Absolute(AnalyticSignal(Data))
Zur Berechnung der Momentanfrequenz verwenden Sie nun folgenden FPScript-Code:
Dim instPhase = PhaseUnwrap(Phase(AnalyticSignal(Data)))
ChangeUnit(1/(2*PI)*Derivative(instPhase), "Hz")
Dies liefert den Frequenzverlauf des Signals:
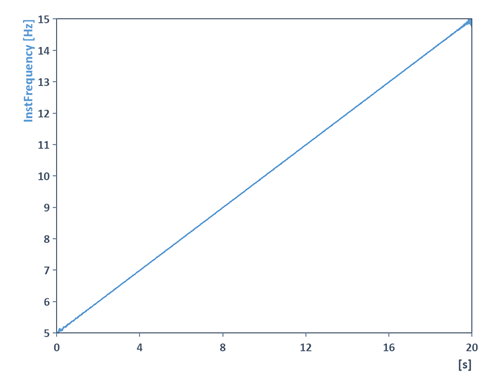
Erstellen Sie nun eine zweite Formel (mit Namen DataWithOffset) in welcher ein Offset bzw. Trend addiert wird.
Beispielsweise: Data + 35
Hinweis Bitte beachten Sie, dass zur Bestimmung des Amplituden-, Phasen-, Frequenzverlaufs oder der Einhüllenden (mit Hilfe obiger Algorithmen), nun eine Trend- bzw. Offsetkorrektur des zu analysierenden Signals erfolgen muss.
Wir berechnen erneut zuerst die Momentanamplitude. Die Trendkorrektur kann im Allgemeinen beispielsweise mit der FPScript-Funktion Trend- oder mittels gleitenden Mittelwerten durch Verwendung der Mean-Funktion realisiert werden:
Dim offset = Trend(DataWithOffset, TREND_CONSTANT)
Absolute(AnalyticSignal(DataWithOffset - offset))
Dies liefert nun den Amplitudenverlauf des mit einem Offset skalierten Signals. Um die Einhüllende zu bestimmen, muss der Trend anschließend allerdings wieder addiert werden. Die Formel muss also geringfügig wie folgt modifiziert werden:
Dim offset = Trend(DataWithOffset, TREND_CONSTANT)
Absolute(AnalyticSignal(DataWithOffset - offset)) + offset
Die liefert die obere Einhüllende des mit einem Offset skalierten Signals:
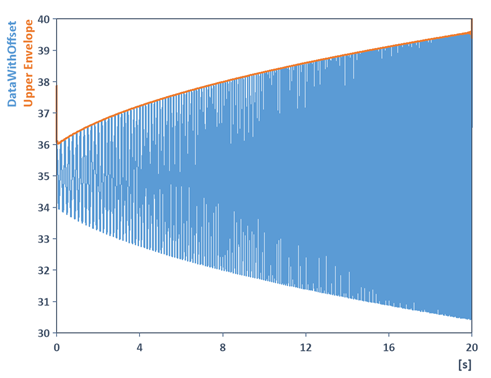
Bitte beachten Sie, dass zur Bestimmung des Frequenzverlaufs analog der Offset subtrahiert werden muss:
Dim offset = Trend(DataWithOffset, TREND_CONSTANT)
Dim instPhase = PhaseUnwrap(Phase(AnalyticSignal(DataWithOffset - offset)))
ChangeUnit(1/(2*PI)*Derivative(instPhase), "Hz")
Bemerkung 1: Bei der Berechnung der Momentanamplitude, Momentanphase, Momentanfrequenz oder Einhüllenden können an den Rändern des Signals (oder allgemeiner in der Umgebung von Sprungstellen des Signals) Seiteneffekte in der Form von Überschwingungen auftreten. Diese Überschwinger lassen sich im oben angegebenen Algorithmus nicht vermeiden und sind rein mathematisch bedingt. Ursache ist das Gibbsche Phänomen, welches bei Fourierreihen und bei der Fourier-Transformation Überschwingungen in der Umgebung von Sprungstellen verursacht.
Bemerkung 2: Für das folgende mit den Beispieldaten von FlexPro zur Verfügung gestellte Signal, liefert obiger Algorithmus zur Bestimmung der oberen Einhüllenden (mit Trendkorrektur mittels der Mean-Funktion) wie erwartet tatsächlich die obere Einhüllende. Das Signal muss dabei nicht einkomponentig sein:
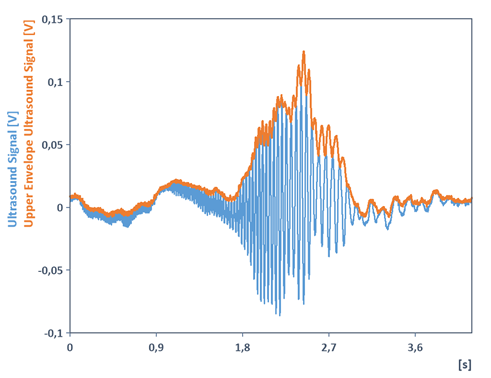
Bemerkung 3: Es ist zu beachten, dass für den Fall mehrkomponentiger Signale, die Interpretationen als Momentanphase und Momentanfrequenz nicht mehr gültig sind. Betrachte dazu folgenden FPScript-Code:
Dim x = Series(0 s, 1 s, 0.001)
Dim y = Sin(2 * PI * x * 30 Hz) + Sin(2 * PI * x * 90 Hz)
Signal(y,x)
Der Algorithmus zur Bestimmung der Momentanfrequenz liefert für diesen Fall eine Mittelung der beiden Sinus-Frequenzen:
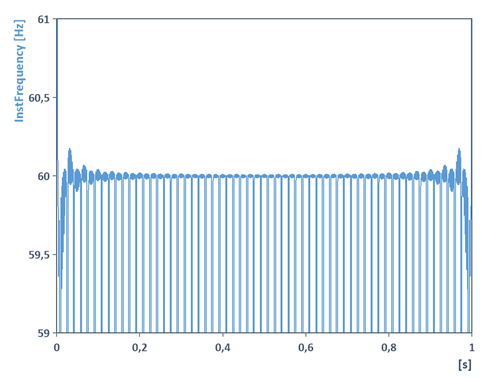
Weitere Anwendung: Demodulation von Signalen (Amplitudendemodulation, Phasendemodulation, Frequenzdemodulation)
Die so definierten Momentangrößen können damit ebenso zur Demodulation von Signalen verwendet werden. Gegeben sei beispielsweise ein moduliertes Signal der Form:
Die Momentanamplitude liefert dann in der Tat den Amplitudenverlauf a(t), wohingegen sich die Momentanphase als Φ(t) berechnet. Mit Hilfe der Momentanfrequenz kann außerdem der Frequenzverlauf des angegebenen Signal bestimmt werden.
Theoretischer Hintergrund: Algorithmus zur Berechnung des analytischen Signals
Die oben angegebene zeitkontinuierliche Berechnungsvorschrift definiert die Übertragungsfunktion H im Frequenzbereich. Der Algorithmus zur Berechnung des diskreten analytischen Signals ist deshalb mit Hilfe der FFT und der diskreten Übertragungsfunktion H wie folgt beschrieben realisiert, siehe insbesondere [1]:
Die Übertragungsfunktion ist für gerade FFT-Längen gegeben als: H[k] = 2 für k = 1, 2, ..., FFTLength/2 - 1 (entspricht den positiven Frequenzen) und H[k] = 0 für k = FFTLength/2 + 1, ..., FFTLength (entspricht den negativen Frequenzen). Sonderstellung nehmen die symmetrischen Koeffizienten k = 0 und k = FFTLength/2 ein. Für diese ist H[k] = 1.
Die Übertragungsfunktion ist für ungerade FFT-Längen analog gegeben als: H[k] = 2 für k = 1, 2, ..., (FFTLength-1)/2 und H[k] = 0 für k = (FFTLength-1)/2 + 1, ..., FFTLength sowie außerdem H[0] = 1.
Der FPScript-Algorithmus zur Berechnung des analytischen Signals ist somit wie folgt festgelegt (das Argument FFTLength muss dabei größer gleich der Datenlänge sein):
Arguments sig, FFTLength
Dim N = NumberOfRows(sig)
Dim fftInput = ComplexFloatingPoint64(sig.Y : (0 # (FFTLength - N)))
Dim fourierTrafo = FFTn(fftInput)
Dim H = 0 # FFTLength
H[0] = 1
If FFTLength Mod 2 == 0 Then
H[FFTLength/2] = 1
H[1, FFTLength/2 - 1] = 2
Else
H[1, (FFTLength - 1)/2] = 2
End
return Signal(IFFTn(H * fourierTrafo)[0, N-1], sig.X)
Einfluss der FFT-Länge: Mittels Zero-Padding, d.h. durch Wahl der FFT-Länge größer als die Datenlänge, wird die Auflösung der für den Algorithmus benötigten FFT erhöht. DasBerechnungsresultat kann dadurch verbessert werden. Ein Beispiel diesbezüglich ist zu finden in der Online-Hilfe zur Hilbert-Funktion.
Literatur
[1] S. Lawrence Marple, Jr., "Computing the Discrete-Time "Analytic" Signal via FFT", IEEE Transactions on Signal Processing, Vol. 47, No.9. http://ieeexplore.ieee.org/iel5/78/16975/00782222.pdf?arnumber=782222,1999.
[2] B. Boashash, "Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals", Proceedings of the IEEE, Vol. 80, No. 4, pp. 519–538. 1992.
[3] Bernard Picinbono, "On Instantaneous Amplitude and Phase of Signals", IEEE Trans. Signal Processing, Vol. 45, No. 3. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.178.833,1997.
Siehe auch
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen