weisang.com > Dokumentation > Analyseobjekt Einhüllende *

FlexPro-Dokumentation

Analyseobjekt Einhüllende *

09.03.2021

Mit diesem Analyseobjekt können Sie die Einhüllende eines Datensatzes berechnen (obere und untere Einhüllende).

Das Analyseobjekt kann Datenreihen, Datenmatrizen, Signale, Signalreihen und Listen verarbeiten.

Zur Berechnung der Einhüllenden stehen drei Algorithmen zur Verfügung: Maximale Steigung, die Peak Einhüllende und die Hilbert-Transformation:

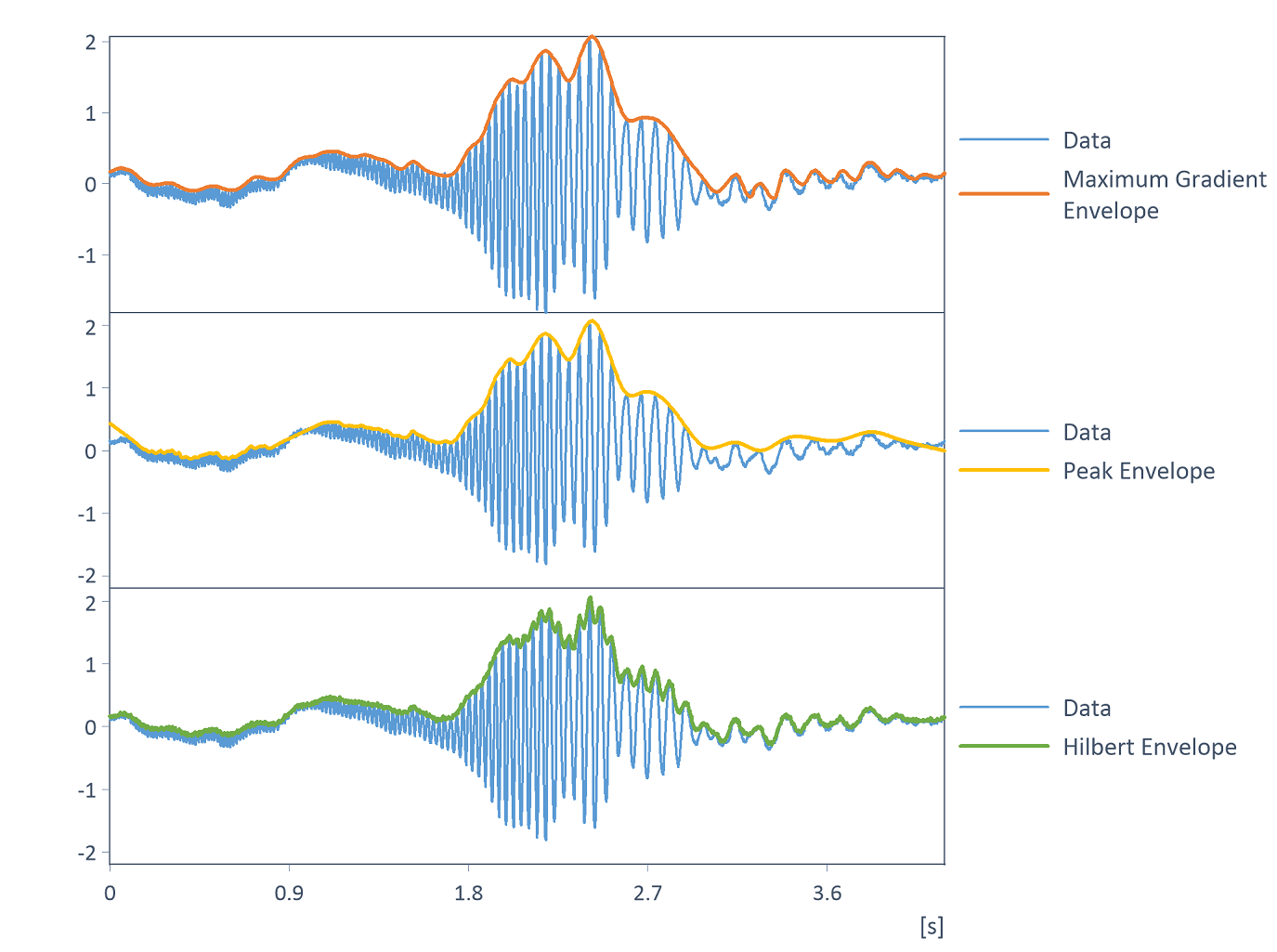
Der Algorithmus Maximale Steigung basiert auf den UpperEnvelope bzw. LowerEnvelope-Funktionen. Beginnend mit dem ersten Datenpunkt werden dabei zu allen Nachbarn eines Intervalls geradlinige Verbindungen berechnet und deren Steigung ermittelt. Der Nachbar mit der höchsten Steigung wird zum nächsten Stützpunkt der Hüllkurve und der Algorithmus wird mit diesem Wert fortgesetzt. Die Intervallbreite kann automatisch berechnet oder manuell eingegeben werden. Die Hüllkurve besitzt dadurch weniger Datenpunkte als der Eingangsdatensatz. Mittels linearer Interpolation lässt sich die Abtastung des Ergebnisses auf die Abtastung des Eingangsdatensatzes erhöhen. Alternativ können die Punkte der Hüllkurve durch Spline-Interpolation geglättet werden.

Der Algorithmus Peak Einhüllende berechnet die Hüllpunkte als lokale Extremstellen (Maxima bzw. Minima) mit Hilfe der Extrema-Funktion. Die Hysterese zur Bestimmung der Extrema kann hierfür spezifiziert werden. Die Hysterese ist der Betrag, um den das Signal vor und nach einem Extremum mindestens ansteigen bzw. abfallen muss, damit der Punkt als Extremum akzeptiert wird. Sie können die Hysterese als Absolutwert oder in Prozent der Spannweite des Datensatzes angeben. Als weiterer Parameter kann zudem eingestellt werden, ob die Randpunkte der Hüllkurve mit den Randpunkten des Eingangsdatensatzes übereinstimmen oder extrapoliert werden sollen. Analog zum Algorithmus Maximale Steigung lässt sich die Abtastung des Ergebnisses mittels linearer Interpolation auf die Abtastung des Eingangsdatensatzes erhöhen oder die Hüllkurve durch Spline-Interpolation glätten.

Der Algorithmus Hilbert-Transformation berechnet die Einhüllende mit Hilfe der Hilbert-Transformation. Dies liefert eine mathematisch exakte Definition der Einhüllenden als Absolutwert des mittels der Hilbert-Transformation berechneten analytischen Signals (siehe auch Berechnung des analytischen Signals). Die Hilbert-Transformation führt intern eine Fourier-Transformation (FFT) des Datensatzes durch. Mittels Zero-Padding, d.h. durch Wahl der FFT-Länge größer als die Datenlänge, wird die Auflösung der für den Algorithmus benötigten FFT erhöht. Das Berechnungsresultat kann dadurch verbessert werden. Im Analyseobjekt lässt sich daher die FFT-Länge bei Bedarf auf die nächste 2er-Potenz erhöhen. Für Signale, die einen Trend bzw. Offset besitzen, muss zur Bestimmung der Einhüllenden mittels der Hilbert-Transformation zusätzlich der Trend im Vorfeld entfernt werden. Die nachfolgend aufgeführten Auswahlmöglichkeiten stimmen mit den Auswahlmöglichkeiten zur Trendentfernung des Analyseobjekts Signalanalyse überein:

Auswahl	Bedeutung
Konstant	Subtrahiert den Mittelwert des Datensatzes.
Linear	Subtrahiert die Bestgerade, d. h. die Gerade für die die Summe der Quadrate der Abweichungen zum Datensatz minimal ist.
Adaptiv	Subtrahiert den Mittelwert aus oberer und unterer Hüllkurve. Die Einstellung kann verwendet werden, wenn der vorliegende Trend weder konstant noch linear ist, sondern zeitabhängig ist.
gleitender Mittelwert	Subtrahiert den gleitenden Mittelwert. Die zur Bildung des gleitenden Mittelwerts benötigte Intervallbreite kann eingegeben werden. Die Einstellung kann verwendet werden, wenn der vorliegende Trend weder konstant noch linear ist, sondern zeitabhängig ist. Der gleitende Mittelwertfilter ist ein Hochpassfilter.
DC-Offset Filter	Hochpassfilter zum Entfernen des DC-Offsets (IIR-Butterworth-Hochpass). Die Grenzfrequenz sowie die Ordnung (d.h. Steilheit) des Hochpassfilters kann eingestellt werden. Das Filter kann verwendet werden, wenn der vorliegende Trend weder konstant noch linear ist, sondern zeitabhängig ist.

Passende Einstellungen zum Entfernen eines zeitabhängigen Trends ist gewöhnlich die Subtraktion des gleitenden Mittelwerts sowie der DC-Offset Filter.