Mit diesem Analyseobjekt können Sie die Rainflow-Matrix oder die Markov-(Übergangs-)Matrix eines Signals ermitteln. Aus den Matrizen können Sie dann mit dem Analyseobjekt Rainflow-Klassierung diverse einparametrige Kollektive, z. B. die Häufigkeiten von Spitzenwerten, extrahieren.

Matrix

Die Markov-Matrix beinhaltet die absoluten Häufigkeiten aller Übergänge in der Belastungs-Zeit-Funktion. Es werden zunächst alle Umkehrpunkte in der Belastungs-Zeit-Funktion ermittelt. Diese Umkehrpunkte werden dann gemäß der Klasseneinteilung klassiert. Als Übergang wird ein Paar aufeinander folgender Umkehrpunkte betrachtet. Die Klasse des "von"-Punktes wählt die Zeile der Matrix aus und die des "nach"-Punktes entsprechend die Spalte. In der sich hieraus ergebenden Matrix-Position wird der Übergang gezählt.

Aus der Markov-Matrix können die Häufigkeiten von Spitzenwerten, Spannen und Klassengrenzenüberschreitungen extrahiert werden. Die Markov-Matrix berücksichtigt die Belange der Betriebsfestigkeitsuntersuchung nicht ausreichend, da größere Lastspiele, in denen kleinere Lastwechsel vorkommen, in eine Folge von kleinen Übergängen zerlegt werden.

Diesen Nachteil umgeht der Rainflow-Algorithmus. Hier werden nicht die Übergänge zwischen aufeinander folgenden Umkehrpunkten gezählt, sondern geschlossene Hysteresen (Spannenpaare). Dies sind Lastwechsel, die ihren Ausgangspunkt mindestens wieder erreichen. Bei einem großen Lastspiel, in dem kleinere Lastwechsel enthalten sind, werden diese also zunächst als kleine Hysteresen gezählt und das große Lastspiel als große Hysterese zum Schluss. Die Hysteresen werden auch als Spannenpaare oder Bereichspaare bezeichnet. Folgende Abbildung zeigt, wie ein Spannenpaar aus der Kurve entnommen wird, ohne dass das große Lastspiel verloren geht:

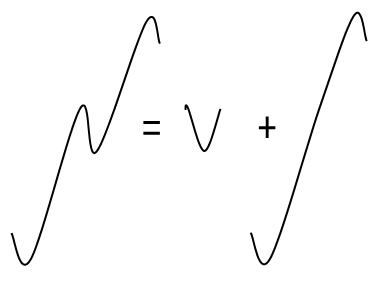
Obige Abbildung zeigt auch, dass ein solches Spannenpaar aus einem aufsteigenden und einem abfallenden Übergang gleicher Größe besteht. In der "von"-"nach" Form der Rainflow-Matrix wird ein solches Spannenpaar deshalb doppelt gezählt, einmal als Anstieg und einmal als Abfall. Alternativ kann auch die asymmetrische Form der Matrix gebildet werden. In diesem Fall wird nur der erste Übergang des Spannenpaares gezählt, der ansteigend oder abfallend sein kann. Diese Form der Matrix unterscheidet also zwischen "positiven" und "negativen" Spannenpaaren. Die Zählsumme der asymmetrischen Matrix ist nur halb so groß wie die der symmetrischen. Man kann die symmetrische Matrix aus der asymmetrischen herleiten, indem man die asymmetrische Matrix mit ihrer Transponierten addiert.

Das Ergebnis der Zählung ist eine Signalreihe mit Z-Komponente. Deren Y-Komponente enthält die Matrix mit den Zählwerten, die X-Komponente die Mitten der "von"-Klassen und die Z-Komponente entsprechend die der "nach"-Klassen. Sie können die Rainflow-Matrix auch in der Spannen-Mittelwert Darstellung ausgeben lassen. In diesem Fall enthält die X-Komponente dann die Untergrenzen der Spannenklassen. In eine Spannenklasse fallen alle Hysteresen mit dem gleichen absoluten Abstand  zwischen "von" und "nach". Die Z-Komponente enthält die Mitten der Mittelwertklassen. In eine Mittelwertklasse fallen alle Hysteresen mit dem gleichen Mittelwert aus "von" und "nach". Auch in diesen Fall werden die geschlossenen Hysteresen nur einfach gezählt.

Residuum

Nachteil des Rainflow-Verfahrens ist die Tatsache, dass nicht alle Umkehrpunkte den Rainflow-Algorithmus erfüllen. Es bleibt oft ein sog. Residuum übrig. Das Residuum ist im Allgemeinen eine Zickzackkurve mit auf- und wieder absteigenden Amplituden. Sie können das Residuum von der Matrix ausschließen, nur eine geschlossene Hysterese "a-b-a" in der Mitte des Residuums in die Matrix aufnehmen das Residuum vollständig in die Matrix aufnehmen. Insbesondere, wenn aus der Rainflow-Matrix einparametrige Kollektive, wie z. B. Spitzenwerte, entnommen werden sollen, sollte das Residuum in die Matrix eingerechnet werden. Hierfür existieren mehrere Verfahren. Das vorliegende, in [1] beschriebene Verfahren ist besonders ausgewogen. Hierbei wird das Residuum am höchsten Punkt zerteilt und die beiden Hälften in umgekehrter Reihenfolge aneinander gehängt. Diese Folge erfüllt dann den Algorithmus und wird in die Matrix eingerechnet. Alternativ können Sie die Halbzyklen des Residuums jeweils mit dem Zählwert 0,5 in die Matrix aufnehmen, d. h. man geht pro Halbzyklus des Residuums vom halben Schädigungsbetrag einer vollen Hysterese aus [2].

Klasseneinteilung

Die Klassierung basiert auf der Einteilung des Wertebereichs der Belastungs-Zeit-Funktion (Quelldatensatz) in diskrete Klassen. Um diese Einteilung vorzunehmen, stehen Ihnen diverse Verfahren zur Verfügung. Im Wesentlichen wird bei allen Verfahren die Lage der Klassengrenzen angegeben. Die Verfahren unterscheiden sich lediglich in der Auswahl der Parameter, die Sie zur Angabe der Klassengrenzen angeben müssen. Die Klassen werden als oben offene Intervalle aus den angegebenen Klassengrenzen gebildet, d. h. die jeweils untere Grenze wird der Klasse zugerechnet. Eine Ausnahme bildet die oberste Klasse, ihr wird auch die obere Grenze zugerechnet. Alle Werte, die über der obersten oder unter der untersten Klasse liegen, werden nicht gezählt!

Die Wahl einer geeigneten Klasseneinteilung muss sorgfältig geplant werden, da nur Ergebnisse, die mit gleicher Klasseneinteilung ermittelt wurden, direkt vergleichbar sind. Lastwechsel in der Belastungs-Zeit-Funktion, die kleiner als die Klassenbreite sind, werden nur dann gezählt, wenn Sie auf einer Klassengrenze liegen. Die Lage der Klassengrenzen hat also Einfluss auf das Zählergebnis.

Hysterese

Um diesen Effekt zu mildern, kann eine Hysterese (Bereichsfilter) zur Unterdrückung kleiner Spannen bzw. Spannenpaare verwendet werden. Die Hysterese ist eine von der Lage der Klassengrenzen unabhängige Größe. Es werden nur die Spannen bzw. Spannenpaare gezählt, deren Amplitude mindestens der Hysterese entspricht. Die Hysterese wird in Prozent der Klassenbreite bzw., bei nicht äquidistanter Klasseneinteilung, der mittleren Klassenbreite angegeben.

Literatur

[1] de Jonge, J.B. (1980). Counting Methods for the Analysis of Load Time Histories. NLR Memorandum SB-80-106 U

[2] ASTM E1049-85(2017). Standard Practices for Cycle Counting in Fatigue Analysis. STM International, West Conshohocken, PA, 2017

Verwendete FPScript-Funktionen

RainflowMatrix

MarkovMatrix

Siehe auch

Option Klassierung

Residuum des Rainflow-Algorithmus

Analyseobjekt Rainflow-Klassierung

Analyseobjekt Klassierung

Analyseobjekt Verbundklassierung