Tutoriel Estimateur Spectral
Ce tutoriel couvre les capacités d'analyse spectrale de FlexPro qui reposent sur la modélisation paramétrique autorégressive et les procédures d'analyse propre. Ces procédures avancées sont particulièrement importantes pour l'estimation de la fréquence lorsque les enregistrements de données sont très courts.
Estimateurs fréquentiels
Les estimateurs spectraux AR et ARMA sont des procédures de modélisation qui utilisent un modèle autorégressif (AR) ou un modèle ARMA (autoregressive-moving average) pour estimer les spectres des données du domaine temporel. L'analyse propre utilise les modes propres du bruit pour reconstruire un spectre de fréquence orthogonal qui ne contient que les composantes du signal à bande étroite. On peut dire que ces trois algorithmes sont des estimateurs de fréquence. C'est-à-dire que ces procédures offrent une estimation très précise des fréquences des harmoniques présentes, mais ces procédures ne donnent généralement pas une mesure précise de la puissance dans les composants.
Extraction de segments stationnaires
Comme ces méthodes sont gourmandes en ressources informatiques, elles sont surtout utiles pour les petits ensembles de données pour lesquels l'analyse de Fourier n'offre pas une résolution suffisante. De plus, les données du signal étant supposées stationnaires, il est parfois utile d'extraire un petit segment d'un flux de données où l'on peut supposer que le signal est approximativement stationnaire (son contenu spectral global ne change pas). Dans ce tutoriel, nous utiliserons un échantillon test de petite longueur de données qui pourrait facilement être une petite pièce dans un échantillon beaucoup plus grand.
Un signal d'essai approprié
Pour ce tutoriel, nous utiliserons un court signal de données de 64 longueurs qui contient trois sinusoïdes espacées de trop près en fréquence pour être résolues par l'analyse de Fourier.
100.0*sin(2π*x*420+p/2)
50.0*sin(2π*x*500+p)
100.0*sin(2π*x*580+3p/2)
La fréquence d'échantillonnage est de 5000 Hz, et par conséquent la fréquence de Nyquist est de 2500 Hz, la fréquence maximale pouvant être détectée. Toute information oscillatoire au-delà de cette fréquence sera aliasée à des fréquences plus basses. Les valeurs de temps varient de 0 à 0,0126 à un incrément de 0,0002 échantillon. Un bruit gaussien aléatoire de 10% a été ajouté. Cela produit un plancher de bruit à environ -30 dB par rapport à la plus grande crête.
La sinusoïde du milieu a une demi-amplitude ou un quart de la puissance des deux autres sinusoïdes. Notez qu'il ne s'agit pas d'un test à gamme dynamique élevée, mais d'un test où les trois pics ont une puissance substantielle. Ce pic central n'est que de -6 dB en dessous des deux autres pics. Ainsi, les optimisations dans le domaine de Fourier auront peu d'impact sur la résolution de ce pic central d'un quart de puissance.
Sélectionnez la commande Fichier > Ouvrir Base de données projet et ouvrez la base de données projet C:\Users\Public\Documents\Weisang\FlexPro\2021\Exemples\Tutoriels\Analyse spectrale.fpd ou C:>Utilisateurs>Public>Documents Public>Weisang>FlexPro>2021>Exemples>Tutoriels>Analyse spectrale.fpd. Ouvrez le dossier Tutoriels et son sous-dossier Estimateurs de fréquence, puis double-cliquez pour ouvrir le graphique 2D appelé Données.
C'est un graphique du signal. Il existe 64 valeurs à virgule flottante.
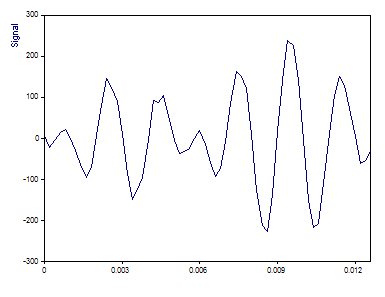
Spectre de Fourier
Nous utiliserons une fenêtre d'observation de données de Hamming pour réaliser l'amortissement maximal des lobes latéraux pour une largeur de Fourier unilatérale de 2.
Fermez la fenêtre du graphique et mettez en évidence l'ensemble de données Signal.
Cliquez sur Insérer[Analyses] > Assistant d'analyse.
Sélectionnez la catégorie Analyse de Fourier sous Analyses spectrales. Ensuite, sélectionnez Spectre de Fourier. Cliquez sur Suivant.
Notez que pour la procédure spectrale, le spectre de Fourier est vérifié. Bien que la procédure spectrale ait été sélectionnée à l'étape 1 de l'assistant d'analyse, elle peut être modifiée à l'étape 2.
Sélectionnez pour le Type de Spectre entrez dB normalisé.
Cela normalise le plus grand pic spectral à 0 dB. Tous les autres pics auront une valeur négative. Un pic à -3 dB aurait la moitié de la puissance du pic à 0 dB, et un pic à -6 dB aurait la moitié de l'amplitude, la valeur attendue pour le milieu des trois pics.
Pour le type de fenêtre, sélectionnez Hamming -43dB W=2.
Dans le module d'analyse spectrale de FlexPro, toutes les fenêtre d'observation de données à largeur fixe (non ajustable) sont répertoriés par leur nom, l'atténuation du lobe latéral en dB, et la largeur du pic du domaine de Fourier unilatéral. Une fenêtre rectangulaire est identique à l'absence de fenêtrage, car tous les éléments de données sont multipliés par l'unité.
Assurez-vous que la longueur de la FFT est réglée sur la longueur des données ou 64.
Le champ d'information Zero Padding indique qu'il n'y a pas eu de rajout de zéro (zero padding).
Sélectionnez l'option Nombre maximal de pics et entrez la valeur 3.
L'assistant d'analyse génère automatiquement des informations sur les pics spectraux. Si cette option est réglée sur 3, les trois pics de puissance les plus élevés seront émis. Notez qu'il est également possible de définir un seuil en dB en dessous du pic le plus important. Pour cet ensemble de données, nous aurions pu tout aussi bien fixer un seuil de -65 dB.
Définissez maintenant le % de limite critique du bruit blanc à Aucun.
Si aucune étiquette n'est visible au-dessus des pics, cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes de fréquence apparaissent.
Vous pouvez choisir parmi plusieurs paramètres. Vous pouvez basculer entre les états des étiquettes, affichant la composante y du spectre (ici, il s'agit de dB normalisés), la composante x (toujours les fréquences), ou aucune information sur les pics.
Le tracé de Fourier dans l'assistant d'analyse devrait être le suivant :
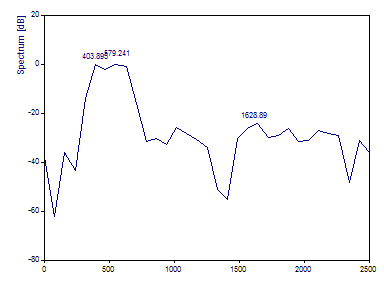
Définissez la longueur de la FFT à 8192.
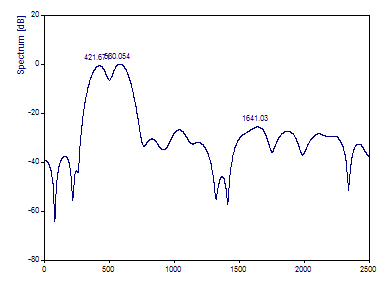
Grâce à l'interpolation introduite par le rajout de zéro (zero padding), les pics de puissance les plus élevés de 420 et 580 sont résolus avec plus de précision, mais la longueur de l'échantillon est trop faible pour produire une quelconque résolution de la sinusoïde de plus faible amplitude de fréquence 500. Rien ne peut être fait pour apporter la résolution nécessaire à l'analyse de Fourier de cet échantillon de données particulier. Ce qu'il faut, c'est échantillonner pendant plus longtemps. Nous allons voir ce qui se passe lorsque ce même flux de données est échantillonné pendant deux fois plus longtemps.
Cliquez sur Annuler. Sélectionnez l'ensemble de données Signal2.
De nouveau, sélectionnez l'Assistant d'analyse. Sélectionnez la catégorie Analyse de Fourier sous Analyses spectrales. Ensuite, sélectionnez Spectre de Fourier. Cliquez sur Suivant. Définissez le Type de spectre à dB normalisé, le Type de fenêtre à Hamming -43dB W=2. Définissez la longueur de la FFT à 8192, le nombre maximum de pics à 3, la Limite critique du bruit blanc à Aucun. Si aucune étiquette n'est visible au-dessus des pics, cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes de fréquence apparaissent.
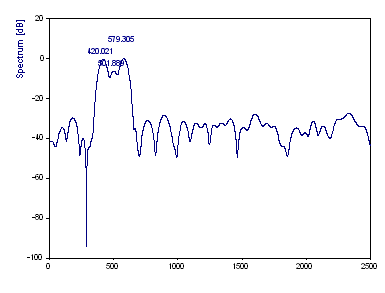
La composante de 420 Hz est détectée à 420.02, la composante de 500 Hz à 501.89, et la composante de 580 Hz à 579.30. Le troisième pic était le plus important en puissance, et est donc à 0 dB. Le premier pic était de -0,21 dB, le pic intermédiaire de -6,20 dB.
À cette longueur d'échantillon, la résolution de Fourier est suffisante pour résoudre les trois composantes. Notez que, bien qu'elle soit à la limite de la résolution, la précision des estimations de fréquence et de puissance est très bonne. Le but de cet exercice est d'illustrer l'intérêt d'explorer en profondeur l'approche de Fourier avant de se tourner vers d'autres procédures.
Mais que se passe-t-il lorsqu'il n'est pas possible d'augmenter l'information contenue dans les données en échantillonnant sur une plus longue période ? Si les données sont un instantané approximativement stationnaire pris à partir d'un signal changeant rapidement, il peut être impossible d'augmenter la résolution en fréquence en utilisant un échantillon plus long. Dans de tels cas, les procédures paramétriques AR et ARMA et l'analyse propre sont nécessaires.
Spectres d'estimation AR
Les méthodes d'estimation de fréquence que nous allons maintenant explorer sont des méthodes puissantes lorsque la longueur des données est trop courte pour une résolution suffisante de l'analyse de Fourier.
Cliquez sur Annuler. Mettre en évidence l'ensemble de données utilisé à l'origine Signal. Il y aura 64 éléments de données.
De nouveau, sélectionnez l'Assistant d'analyse. Sélectionnez la catégorie Estimateur spectral sous Analyses spectrales. Ensuite, sélectionnez Estimateur spectral AR. Cliquez sur Suivant.
Sélectionnez l'algorithme Matrice données FB SVD.
Les procédures d'autocorrélation, de Burg, d'équations normales FB et de Data Matrix FB n'offrent aucune séparation signal-bruit intrinsèque. Elles sont proposées dans FlexPro à des fins d'analyse comparative et parce que ces procédures ont été historiquement utilisées pour les analyses AR. Ces procédures peuvent produire des pics parasites, des pics dédoublés et d'autres anomalies qui sont dangereuses dans l'analyse spectrale. Seules les procédures FB SVD Equations normales et FB SVD Data Matrix sont recommandées.
La procédure Équations normales FB SVD peut être nécessaire si les délais de traitement sont excessifs. Elle est beaucoup plus rapide que la procédure SVD de Data Matrix FB sur de très longs ensembles de données.
Définissez le Type de Spectre à dB. Définissez l'Ordre à 40 et le sous-espace de signal à 6.
L'ordre de 40 signifie qu'un modèle AR de 40 coefficients sera généré. Un espace de signal de 6 signifie que seuls 6 des modes propres seront traités comme un signal. Les 34 autres modes propres seront traités comme du bruit et rejetés dans le calcul SVD des coefficients AR. La séparation signal-bruit intrinsèque élimine l'influence du bruit sur le spectre.
Ce seuillage intrinsèque signal-bruit élimine l'influence du bruit dans les spectres. Notez que vous devez spécifier un espace de signal de 2 pour chaque composante oscillatoire à bande étroite dans les données. Pour détecter trois harmoniques dans les données, l'espace du signal doit être réglé sur deux fois ce nombre, soit 6. Notez également qu'il n'y a pas de spécification du nombre de pics avec les spectres AR, car le nombre de pics est déterminé par les racines du polynôme AR pour les algorithmes non UDS, et par l'espace du signal pour les procédures UDS.
Sélectionnez l'option Espacement adaptatif.
L'option d'espacement adaptatif fournit un spectre à gamme de fréquences complète qui est adaptatif, avec de nombreux points où les pics sont nets et la magnitude spectrale change rapidement, et moins de points où la magnitude spectrale change lentement.
Si aucune étiquette n'est visible au-dessus des pics, cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes de fréquence apparaissent.
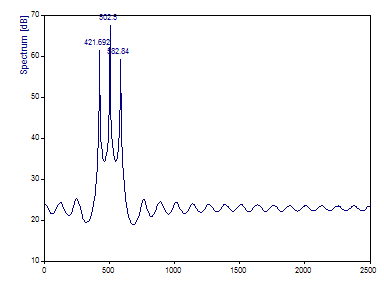
Alors que l'analyse de Fourier n'a rien pu faire pour résoudre l'harmonique de fréquence intermédiaire, une analyse spectrale AR correctement conçue permet de retrouver clairement les trois composantes spectrales. Les pics spectraux très nets sont typiques des harmoniques dans les spectres AR.
La composante de 420 Hz est estimée à 421,69, celle de 500 Hz à 502,5 et celle de 580 Hz à 582,84. Bien que très impressionnants par rapport aux spectres de Fourier de ce même échantillon de 64 points, notez que l'analyse de Fourier de l'échantillon de 128 points a produit des estimations de fréquence plus précises. Notez également que les amplitudes des pics de RA sont l'inverse du profil de puissance ou d'amplitude. La composante centrale est celle qui a la plus grande magnitude dans le spectre. C'est pourquoi la méthode AR doit être considérée avant tout comme un estimateur de fréquence uniquement. Là encore, la procédure en deux étapes de l'option Analyse harmonique doit être utilisée pour estimer les amplitudes et les puissances des composantes.
Sélectionnez maintenant l'algorithme Matrice de données FB.
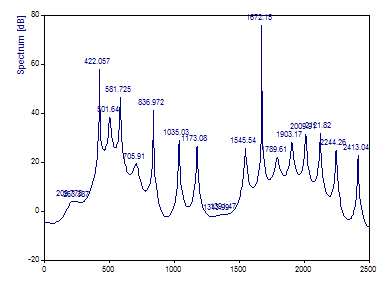
C'est plutôt ce que l'analyse spectrale AR conventionnelle a donné historiquement, et c'est pourquoi elle a une mauvaise réputation dans de nombreux milieux. À moins qu'il n'y ait une séparation signal-bruit intrinsèque dans les calculs du coefficient AR, un modèle AR produira généralement la moitié de l'ordre du modèle en pics, et il n'est pas rare que certains d'entre eux soient parasites. On constate qu'un pic de bruit a une magnitude spectrale supérieure à celle des trois pics de la cible.
Sélectionnez la méthode d'autocorrélation.
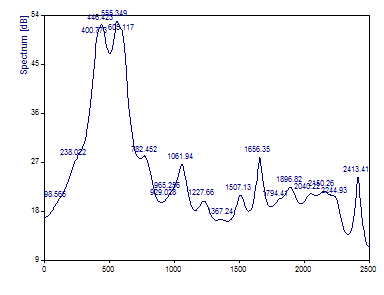
Comme le filtre AR issu de cette procédure est toujours stable (les racines complexes du polynôme AR sont toujours à l'intérieur ou sur le cercle unitaire), les pics parasites des autres algorithmes non-SVD ont tendance à se produire moins souvent, mais cette méthode a une résolution en fréquence nettement inférieure. Notez que cette méthode AR est incapable de résoudre la composante centrale.
Spectres d'analyse propre
Les méthodes d'analyse propre sont généralement considérées comme la classe la plus précise d'estimateurs de fréquence. Les algorithmes MUSIC (MUltiple SIgnal Classification) et Eigenvector sont largement utilisés pour estimer avec précision les composantes à bande étroite des signaux.
Sélectionnez la procédure spectrale Eigen (MUSIC, EV) et pour l'algorithme MUSIC. Assurez-vous que le Type de spectre est réglé sur dB, que l'Ordre est réglé sur 40 et que le Sous-espace du signal est à 6. Conservez l'option Espacement adaptatif.
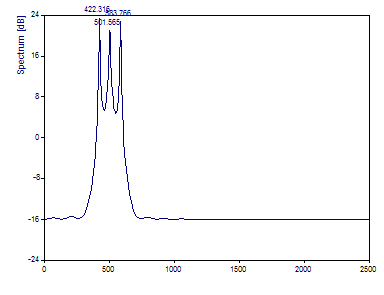
La composante de 420 Hz est estimée à 422,32, celle de 500 Hz à 501,56 et celle de 580 Hz à 583,77. Bien qu'à nouveau impressionnante par rapport aux spectres de Fourier de ce même échantillon de 64 points, l'analyse de Fourier de l'échantillon de 128 points a produit des estimations de fréquence plus précises.
En outre, ces estimations ne sont pas tout à fait aussi précises que la procédure AR. Ici, cependant, la composante centrale est montrée comme ayant une magnitude plus faible dans le spectre. Bien qu'il s'agisse du profil correct dans ce cas, les méthodes d'analyse propre ne doivent être considérées que comme des estimateurs de fréquence. Là encore, la procédure en deux étapes de l'option Analyse harmonique doit être utilisée pour estimer les amplitudes et les puissances des composantes.
Sélectionnez l'algorithme EV (EigenVector).
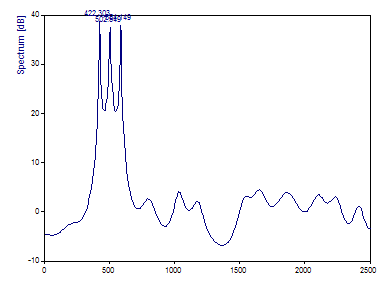
La composante de 420 Hz est estimée à 422,30, celle de 500 Hz à 502,55 et celle de 580 Hz à 584,14. Pour ces données, la procédure MUSIC a été légèrement plus efficace pour récupérer les fréquences sous-jacentes.
Dans ces procédures, les modes propres du bruit sont utilisés pour générer les spectres du signal, et en tant que tels, il devrait toujours y avoir un nombre élevé de modes propres du bruit pour cartographier suffisamment le bruit dans ce signal. La différence entre les algorithmes MUSIC et EV réside uniquement dans la façon dont les différents modes propres du bruit sont pondérés.
Estimation harmonique
Nous allons maintenant employer une analyse harmonique en deux étapes pour extraire les amplitudes et la puissance des composantes spectrales.
Cliquez sur Précédent. Sélectionnez les Analyses harmoniques, puis sélectionnez Estimation harmonique. Cliquez sur Suivant.
Sélectionnez l'algorithme Matrice de données FB SVD, réglez le nombre de composants sur le nombre maximum. Définissez le nombre maximum à 3 et le Type de Spectre à Composantes Harmoniques. Définissez l ordre à 32.
Un ordre inférieur doit être spécifié dans cette procédure en deux étapes. Des anomalies peuvent se produire si l'ordre du modèle est poussé au-delà de la moitié de la longueur des données. Pour se protéger contre ces effets qui ne sont pas facilement observés dans cet algorithme automatisé en deux étapes, FlexPro limite les ordres du modèle dans le spectre harmonique à la moitié de la longueur des données.
Cliquez sur Basculer les étiquettes jusqu'à ce que les étiquettes d'amplitude apparaissent.
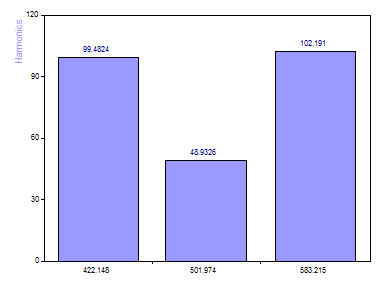
Notez que les amplitudes [100, 50, 100] sont récupérées à quelques pour cent près.
Cliquez sur Suivant. Sélectionnez tous les objets de l'étape 3. Cliquez sur Terminer.
Double-cliquez sur l'objet HarmonicEstimation dans la liste des objets de FlexPro.
Les phases utilisées dans les signaux originaux étaient π/2, π, 3π/2. Il est typique que les plus petites erreurs se produisent dans les fréquences et les plus grandes erreurs dans les phases. Ici, la phase 1.57 est 1.49, la phase 3.14 est 2.94 et la phase 4.71 est 4.58. Ce résultat est encore très bon, étant donné qu'un bruit aléatoire de 10% a été ajouté à ce signal de test.
Références
Une excellente documentation sur les algorithmes spectraux AR peut être trouvée dans les références suivantes :
•S. Lawrence Marple, Jr., "Digital Spectral Analysis with Applications", Prentice-Hall, 1987, p.172-284.
•Steven M. Kay, "Modern Spectral Estimation", Prentice Hall, 1988, p.153-270.
L'information sur l'algorithme de Burg peut également être intéressante :
•W. H. Press, et. al, "Numerical Recipes in C", Cambridge University Press, 1992, p.564-575.
Une bonne couverture des algorithmes spectraux d'analyse propre peut être trouvée dans les références suivantes :
•S. Lawrence Marple, Jr., "Digital Spectral Analysis with Applications", Prentice-Hall, 1987, p.361-378.
•Steven M. Kay, "Modern Spectral Estimation", Prentice Hall, 1988, p.429-434.