weisang.com > Dokumentation > Modélisation autorégressive

Documentation FlexPro

Modélisation autorégressive

23.08.2021

Auto-régression

Si un modèle peut être ajusté avec succès à un flux de données, il peut être transformé dans le domaine des fréquences à la place des données sur lesquelles il est basé, produisant un spectre continu et lisse. C'est le principe de base des spectres produits par la modélisation autorégressive (AR). Dans un modèle AR, une valeur au moment t est basée sur une combinaison linéaire de valeurs antérieures (prédiction avant), sur une combinaison de valeurs ultérieures (prédiction arrière), ou sur les deux (prédiction avant-arrière). Les modèles linéaires donnent lieu à des calculs rapides et robustes.

Définitions AR et ARMA

Afin de préserver les degrés de liberté pour les tests statistiques et de fournir une référence commune pour tous les algorithmes AR, FlexPro définit un modèle AR comme suit :

Dans ces équations, x est la série de données de longueur N et a est le tableau de paramètres autorégressifs d'ordre p. FlexPro utilise la convention de signe positif (prédiction linéaire) pour les coefficients AR. Le modèle est défini comme une prédiction inverse pour les premières valeurs p, et une prédiction directe pour les N - p valeurs restantes. Cette définition est utilisée pour toutes les statistiques d'ajustement AR, bien qu'il ne s'agisse pas du modèle ajusté dans l'une des procédures des moindres carrés linéaires AR. Ce modèle n'est ajusté que si un ajustement non linéaire AR-only est effectué dans la procédure ARMA.

La définition ARMA est également celle qui préserve les degrés de liberté :

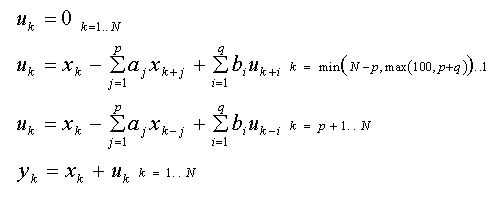
Ici, b est le tableau des paramètres de la moyenne glissante d'ordre q. Les calculs commencent à nouveau par une prédiction inverse, mais un indice de départ plus élevé est utilisé pour inclure une moyenne glissante dans les premières valeurs p. Ce modèle est ajusté dans les algorithmes ARMA non linéaires.

Définitions spectrales AR

Les fonctions de densité spectrale de puissance AR et ARMA sont définies comme suit :

Dans ces équations, ν est la variance du bruit blanc d'entraînement et δt est l'intervalle d'échantillonnage. Notez que les deux modèles spectraux sont des fonctions continues de la fréquence.

Classes d'algorithmes AR

Les coefficients AR peuvent être calculés de différentes manières. Les coefficients peuvent être calculés à partir d'estimations d'autocorrélation, de coefficients d'autocorrélation partielle (réflexion) et de procédures de matrice des moindres carrés. En outre, un modèle AR utilisant la méthode d'autocorrélation dépendra du seuil de troncature (décalage maximal) utilisé pour calculer les corrélations. La méthode d'autocorrélation partielle dépendra de la définition spécifique du coefficient de réflexion. Les méthodes des moindres carrés donneront également des résultats qui sont fonction de la façon dont les données sont traitées aux limites (taille de la matrice) ainsi que de l'ajustement de la matrice de données ou des équations normales.

La plupart des algorithmes AR de FlexPro sont des procédures de moindres carrés car ils produisent les meilleures estimations spectrales. Les méthodes des moindres carrés qui offrent une séparation in-situ du signal et du bruit par la décomposition de la valeur singulière (SVD) sont les plus robustes des méthodes AR de FlexPro. Ces algorithmes sont intégrés dans les procédures AR (il n'y a pas, par exemple, d'option séparée Principal Component AutoRegressive ou PCAR).

Modèles de prédiction AR

Une fonction continue du temps n'a besoin que des paramètres calculés du modèle pour produire une estimation pour toute valeur de temps souhaitée. Le fait que l'échantillonnage temporel original soit uniforme ou irrégulier n'entre pas en ligne de compte une fois le modèle généré. Ceci n'est pas vrai pour un modèle autorégressif. Un modèle de prédiction linéaire AR est une fonction discrète qui nécessite des données uniformément échantillonnées.

Lorsqu'un modèle AR est évalué dans le domaine temporel pour une valeur prédite future, la dernière partie de la séquence de données est filtrée par les coefficients AR pour générer un nouvel élément. Bien qu'un modèle de prédiction linéaire AR ne contienne pas explicitement une composante de bruit, celle-ci fait intrinsèquement partie de la séquence de données. Le bruit blanc est donc géré, à condition qu'il soit non corrélé, point par point.

Limites du modèle AR

Dans la pratique, il peut être impossible de prédire une valeur actuelle à partir des valeurs passées. Le processus peut être stochastique (véritablement aléatoire) plutôt que déterministe. Il peut n'y avoir aucune corrélation entre les valeurs passées et la valeur actuelle.

Le bruit de fond n'est pas non plus nécessairement blanc et non corrélé. Les processus géophysiques, par exemple, sont souvent caractérisés par un bruit de fond rouge. Pour le bruit rouge, la variance diminue avec l'augmentation de la fréquence. Dans certains cas, la tendance générale du bruit peut être approximée par un modèle AR du premier ordre.

Plus l'ordre du modèle AR augmente, plus les tendances des séries de données sont incorporées. Lorsque le bruit est totalement absent, les harmoniques pures sont capturées avec un ordre égal à deux fois le nombre de composantes. Le plus souvent, cependant, un certain niveau de bruit est présent.

En outre, les signaux à bande étroite sont souvent anharmoniques. Les composantes du signal seront proches de l'harmonique, mettant en évidence des oscillations régulières, mais ne pourront pas être décrites par une sinusoïde unique ou une sinusoïde à amortissement exponentiel. L'information nécessaire pour décrire la tendance oscillatoire peut exiger que le modèle AR capture plusieurs cycles de l'oscillation. Pour les modèles à évolution lente, cela peut signifier des commandes de modèles appréciables.

Séparation Signal-bruit AR

L'ajustement d'un modèle AR de base n'offre pas une partition signal-bruit efficace. Même si des sinusoïdes pures sont intégrées dans des niveaux de bruit modestes, il peut être nécessaire d'atteindre un ordre bien supérieur au double du nombre de composants du signal pour réussir à capturer et à restituer spectralement les sinusoïdes. En d'autres termes, si l'ordre du modèle est trop faible, seule une partie du signal déterministe est capturée. Le reste est traité comme faisant partie du bruit blanc. Les composantes spectrales sont donc manquées.

D'autre part, si l'ordre du modèle est trop élevé, le signal déterministe complet est capturé mais une certaine mesure du bruit est également modélisée. Des pics spectraux parasites peuvent en résulter.

Il existe trois façons de gérer cette limitation. Tout d'abord, le bruit peut être filtré ou supprimé avant l'analyse. Deuxièmement, on peut déterminer un ordre AR optimal qui capture tous les éléments déterministes du signal et inclut le moins de bruit possible. La troisième option consiste en une suppression du bruit in-situ dans les procédures des moindres carrés qui génèrent les coefficients. Cette dernière option est recommandée.

Sélection du mode propre du signal

Plutôt que de s'efforcer de trouver un ordre de modèle optimal, une séparation signal-bruit explicite peut être effectuée. Plus l'ordre AR augmente, plus il y a de coefficients pour représenter à la fois les tendances des données et le bruit. Si une procédure matricielle basée sur les composantes principales est ensuite utilisée, les vecteurs propres initiaux ne décriront que les composantes du signal. Ces derniers vecteurs propres captureront les contributions du bruit. L'ordre du modèle est alors moins important, puisque les vecteurs de bruit sont éliminés avant le calcul des coefficients AR.

Cette séparation signal-bruit in situ est réalisée en utilisant la décomposition en valeurs singulières (SVD) dans les modèles AR des moindres carrés. Cette option est présente dans toutes les procédures AR et ARMA qui utilisent SVD. Les modes propres retenus doivent représenter le signal ou les composantes principales puisque ceux-ci sont utilisés pour la solution de la procédure. Les modes propres écartés devraient représenter le bruit puisque cette information est mise à zéro et n'entre pas dans la solution. Cette séparation signal-bruit est intrinsèque aux procédures SVD. Pour l'analyse des composantes en bande étroite, il faut noter que deux modes propres du signal sont nécessaires pour chaque sinusoïde. Si un signal contient trois composantes harmoniques principales, le sous-espace du signal doit être fixé à six.

Spectres continus AR

Les spectres AR dans le domaine fréquentiel n'impliquent pas de filtrage de la série originale, sauf pour déterminer une mesure globale du bruit blanc. C'est pourquoi les spectres de fréquence des AR sont si lisses. Idéalement, les coefficients AR ne modélisent que les tendances des données, tandis que le bruit est traité comme une constante dont la valeur est égale à la variance du bruit blanc ou à la puissance de l'erreur déterminée par l'ajustement. La transformée AR en fréquence n'utilise que les coefficients AR et cette variance de bruit blanc, et le résultat est une fonction continue de la fréquence.

Chaque algorithme FlexPro AR produit donc une estimation de la variance en bruit blanc. Cette variance a un impact sur la magnitude, mais pas sur la forme des composantes spectrales. Les erreurs d'estimation de la variance de ce bruit blanc se traduisent par des erreurs d'échelle des valeurs spectrales AR. Les algorithmes de Burg et d'Autocorrélation génèrent généralement des erreurs de prédiction normalement distribuées et des spectres AR dont l'intégrale est très proche de la puissance des données. Les procédures de moindres carrés peuvent ne pas le faire.

Un ajustement AR réussi aux composantes du signal dans les données peut souvent être obtenu en utilisant des enregistrements de données très courts, et un spectre à très haute résolution peut en résulter. Un estimateur spectral AR peut comporter des pics extrêmement nets, et pour les meilleurs algorithmes, ceux-ci seront présents à une fréquence proche de la fréquence exacte de la composante à bande étroite. Dans un modèle AR, les fréquences sont déterminées directement à partir des racines AR du modèle. Il n'est pas nécessaire de recourir à une procédure de détection des maxima locaux.

En comparant les méthodes AR et FFT, ces dernières sont résolument simples et robustes. Une FFT peut nécessiter une certaine optimisation en termes de sélection des fenêtres, de longueur et de chevauchement des segments, ou de rajout de zéro (zero padding), mais il est difficile d'obtenir une réponse incorrecte. En outre, la plupart des raffinements nécessaires pour affiner un algorithme FFT sont intuitifs. Ce n'est pas nécessairement le cas pour les spectres AR.