Surface Interpolation Analysis Object *
This analysis object offers you four methods for the interpolation, i.e., smoothing, of surfaces.
The 2D spline interpolation, and the compensating 2D spline interpolation use the same mathematical methods as the one-dimensional spline interpolation, which is described in more detail under that topic. A two-dimensional data set, however, is a grid of points that is interpolated one after another in an X and Z direction. The boundary conditions and the evaluation mode can be set separately for both directions.
The bicubic spline interpolation interpolates the data grid in one step. A bicubic spline function is used for each "tile" of the data grid. The method is efficient, robust and results in surfaces that are smooth between as well as at the data points. However, no boundary conditions can be set.
The "Natural Neighbor" interpolation is a modern method that generates natural looking surfaces that are smooth between the data points, but not at the data points. The result resembles a rubber mat that was pulled over the data. The algorithm calculates for each sampling point a weighted mean value over all natural neighbors of this point.
"Natural neighbor" interpolation is the only method with which you can interpolate scatter data, i.e., data with any number of X and Z coordinates. In this case, the data set to be interpolated is a space curve. If your data exists as a data grid, i.e., as a signal series or data matrix, then you can use any of the three methods for interpolation.
"Natural neighbor" interpolation offers the variants extrapolating and convex. In extrapolating mode, all grid points in the result are occupied even for space curves that span a convex surface, and for data matrices that have void values at the edges. In convex mode, the points outside the convex envelope are filled with void values.
Bicubic spline interpolation and "natural neighbor" interpolation are directly integrated into the 3D surface graph of FlexPro so that you only use this analysis object when you want to process the smoothed data further mathematically.
The following illustration shows the different types of interpolation:
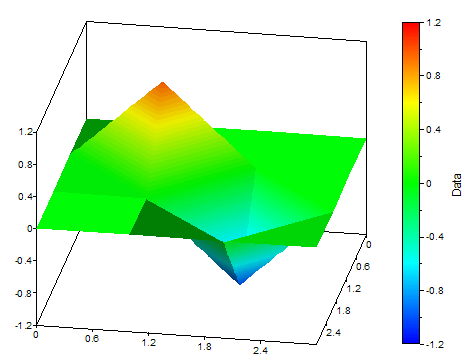
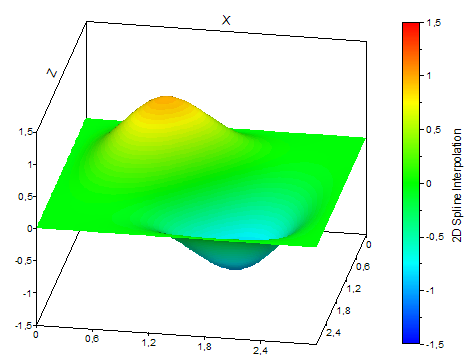
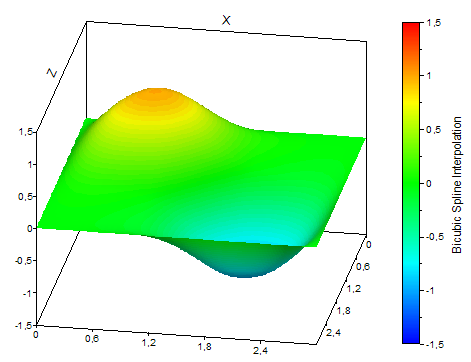
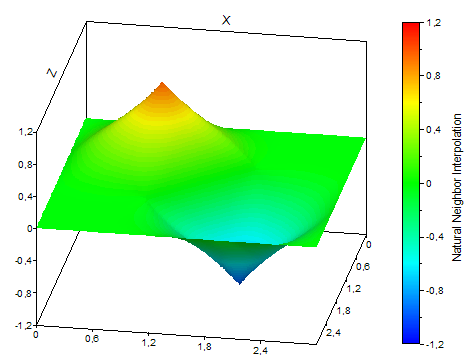
FPScript Functions Used
See Also
2D Approximation Analysis Object
Curve Transformation Analysis Object
* This analysis object is not available in FlexPro View.
You might be interested in these articles
You are currently viewing a placeholder content from Facebook. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou need to load content from reCAPTCHA to submit the form. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from Instagram. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from X. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information