CompensatingSpline2D (FPScript)
Interpolates a two-dimensional data set through a grid of compensating spline curves and samples these curves at definable points.
Syntax
CompensatingSpline2D(Surface, NX, NZ, SamplingMode, Weighting)
or
CompensatingSpline2D(DataMatrix, LocusX, LocusZ, NX, NZ, SamplingMode, Weighting)
The syntax of the CompensatingSpline2D function consists of the following parts:
Part |
Description |
||||||
|---|---|---|---|---|---|---|---|
Surface |
The data matrix or signal series with a Z component and a constant sampling interval, which is interpolated. If the X and Z components are missing, they will be generated automatically. Permitted data structures are data matrix und signal series. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||
DataMatrix |
Data matrix with the Y component of the signal series to be interpolated. If you specify a signal series, then its Y component is used. Permitted data structures are data matrix und signal series. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
LocusX |
Data series with the X component of the signal series to be interpolated. If you specify a signal, then its Y component is used. Permitted data structures are data series und signal. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
LocusZ |
Data series with the Z component of the signal series to be interpolated. If you specify a signal, then its Y component is used. Permitted data structures are data series und signal. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
NX |
Specifies the total number of points or per X interval of the signal series. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 0. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
NZ |
Specifies the total number of points or per Z interval of the signal series. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 0. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
SamplingMode |
Specifies how the calculated spline surface is to be sampled. The argument SamplingMode can have the following values:
If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
Weighting |
Specifies the compensation measure for the spline surface. Values close to zero result in a straight line, and very high values result in a natural spline surface. Permitted data structures are scalar value. All real data types are permitted. The value must be greater or equal to 0. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
Remarks
The result always has the data type 64-bit floating point.
The result has the same unit as the argument Surface.
First, for each row of the grid given by the Y component of the data set, a compensating spline curve is modeled and evaluated at the desired Z positions. This type of spline curve consists of cubic polynomials, which are appended to one another to provide the smoothest course possible. Then, for each column of the data matrix calculated this way, a spline curve is modeled and evaluated at the desired X positions. In the approximating spline function, the polynomials do not necessarily pass through the points of the data set, but instead they even them out. The compensating measure can be varied by the natural spline surface, which passes through the points, up to the best approximated plane. Before every spline interpolation, void values in rows or columns are eliminated by linear interpolation. The Y component of the data set to be interpolated must contain at least 3 x 3 values, and the X and Z components must be strictly increasing.
The following illustrations show two compensating 2D spline surfaces with different weightings and the data on which they are based:
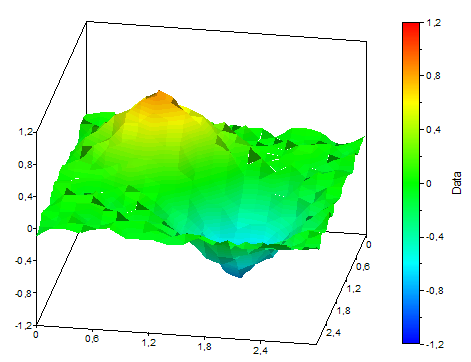
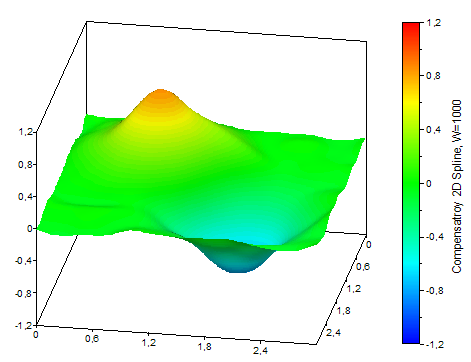
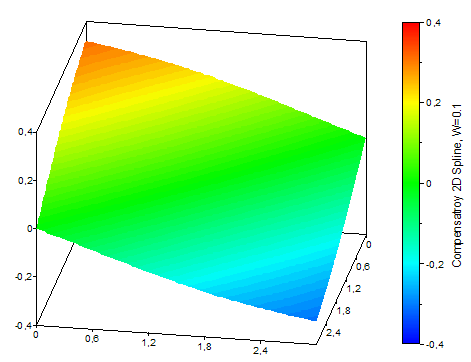
Available in
FlexPro Basic, Professional, Developer Suite
Examples
CompensatingSpline2D({{0, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, -1, 0}, {0, 0, 0, 0}}, 100, 100, SPLINE_EQUIDISTANT, 1000) |
Interpolates the data matrix through a grid of compensating spline curves with a high weighting. |
See Also
Spline Interpolation Analysis Object
Surface Interpolation Analysis Object
2D Approximation Analysis Object
References
[1] "Carl de Boor": "A Practical Guide to Splines, Revised Edition". "Springer-Verlag, New York",2001.ISBN 0-387-95366-3.
You might be interested in these articles
You are currently viewing a placeholder content from Facebook. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou need to load content from reCAPTCHA to submit the form. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from Instagram. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from X. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information