BicubicSpline (FPScript)
Interpolates a two-dimensional data set through a bicubic spline surface and samples this spline surface at definable points.
Syntax
BicubicSpline(Surface, NX, NZ, SamplingMode)
or
BicubicSpline(DataMatrix, LocusX, LocusZ, NX, NZ, SamplingMode)
The syntax of the BicubicSpline function consists of the following parts:
Part |
Description |
||||||
|---|---|---|---|---|---|---|---|
Surface |
The data matrix or signal series with a Z component and a constant sampling interval, which is interpolated. If the X and Z components are missing, they will be generated automatically. Permitted data structures are data matrix und signal series. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||
DataMatrix |
Data matrix with the Y component of the signal series to be interpolated. If you specify a signal series, then its Y component is used. Permitted data structures are data matrix und signal series. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
LocusX |
Data series with the X component of the signal series to be interpolated. If you specify a signal, then its Y component is used. Permitted data structures are data series und signal. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
LocusZ |
Data series with the Z component of the signal series to be interpolated. If you specify a signal, then its Y component is used. Permitted data structures are data series und signal. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
NX |
Specifies the total number of points or per X interval of the signal series. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 0. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
NZ |
Specifies the total number of points or per Z interval of the signal series. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 0. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
SamplingMode |
Specifies how the calculated spline surface is to be sampled. The argument SamplingMode can have the following values:
If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
Remarks
The result always has the data type 64-bit floating point.
The result has the same unit as the argument Surface.
A modeled spline surface consists of bicubic polynomials that are appended to one another to provide the smoothest course possible.
The Y component of the data set to be interpolated must contain at least 3 x 3 values.
In the sampling mode SPLINE_EQUIDISTANT, the X and Z components of the data set to be interpolated must be strictly increasing. In the sampling mode SPLINE_INTERVAL, however, strictly decreasing X and Z values are also allowed. Before the spline interpolation, void values in the Y data matrix are eliminated by linear interpolation.
The following illustrations show a bicubic spline surface and the data on which it is based:
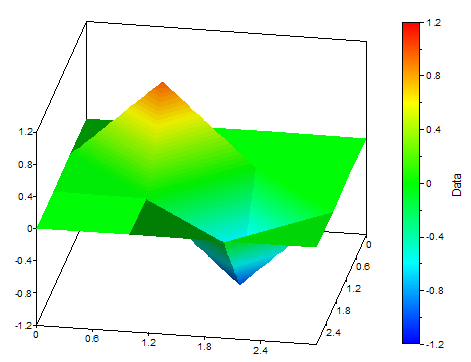
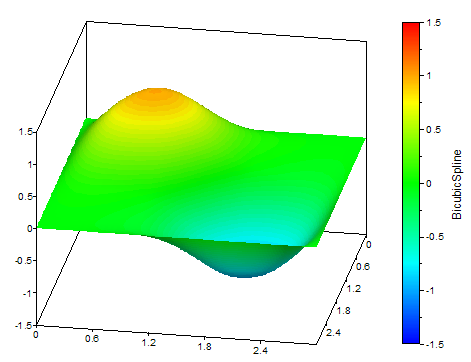
Available in
FlexPro Basic, Professional, Developer Suite
Examples
BicubicSpline({{0, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, -1, 0}, {0, 0, 0, 0}}, 100, 100, SPLINE_EQUIDISTANT) |
Interpolates the data matrix through a bicubic spline surface. |
See Also
Spline Interpolation Analysis Object
Surface Interpolation Analysis Object
2D Approximation Analysis Object
References
[1] "Hiroshi Akima": "A Method of Bivariate Interpolation and Smooth Surface Fitting Based on Local Procedures". In: "Communications of the ACM, Volume 17, Issue 1, Pages: 18 - 20". 1974.