PolynomialInterpolation (FPScript)
Carries out polynomial interpolation at predefinable sampling points. Polynomial interpolation is understood to be the search for a polynomial that runs exactly through the predefined points.
Syntax
PolynomialInterpolation(DataSet)
or
PolynomialInterpolation(DataSet, X)
or
PolynomialInterpolation(DataSet, N, SamplingMode)
The syntax of the PolynomialInterpolation function consists of the following parts:
Part |
Description |
||||||
|---|---|---|---|---|---|---|---|
DataSet |
Specifies the sampling points for which the interpolation is to be carried out. If you specify a data series, then the X component will be generated automatically. The calculated polynomial goes exactly through all sampling points. Permitted data structures are data series, data matrix, signal und signal series. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||
X |
Specifies a data set with the X values for which the polynomial is evaluated. Permitted data structures are scalar value und data series. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||
N |
Specifies the total number of points or per X interval of the signal. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 1. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
SamplingMode |
Specifies how the calculated polynomial is to be sampled. The argument SamplingMode can have the following values:
If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
Remarks
The result always has the data type 64-bit floating point.
If the function is called using only the DataSet argument, the function returns the polynomial coefficients. In the other two cases, the interpolated signal is returned. For n sampling points, a polynomial of the n - 1 degree is determined. Polynomial interpolation is also known as Lagrange interpolation. The Neville algorithm is used for the calculation.
Available in
FlexPro Basic, Professional, Developer Suite
Examples
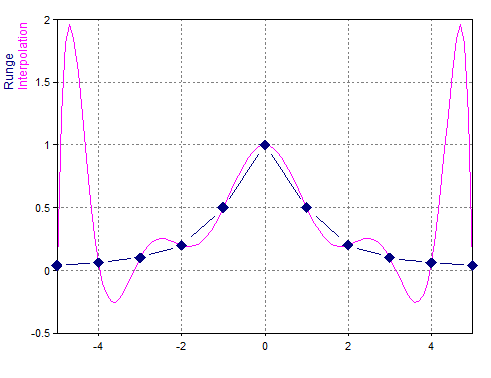
Dim x = Series(-5,5,1)
Dim runge = Signal(1. / (1 + x ^ 2), x)
PolynomialInterpolation(runge, Series(runge.x[0], runge.x[-1], 0.1))
Carries out polynomial interpretation of the Runge function (n=11) with a sampling rate of 0.1.
PolynomialInterpolation(runge, 100, POLYNOMIALINTERPOLATION_EQUIDISTANT)
Carries out polynomial interpretation of the Runge function (n=11) with 100 equidistantly sampled values.
PolynomialInterpolation(runge)
Returns the coefficients of the polynomial interpolation of the Runge function (n=11).
See Also
Spline Interpolation Analysis Object
Surface Interpolation Analysis Object
References
[1] "William H. Press et al.": Numerical Recipes in C, Second Edition, page 108-122. "Cambridge University Press",1992.ISBN 0-552-43108-5.
