Isoline (FPScript)
Determines one or more isolines from a data matrix or signal series.
Syntax
Isoline(DataSet, Level [ , Result = ISOLINE_2D ])
The syntax of the Isoline function consists of the following parts:
Part |
Description |
||||||
|---|---|---|---|---|---|---|---|
DataSet |
The data set for which the isoline is to be calculated. Permitted data structures are data matrix und signal series. All numeric data types are permitted. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||
Level |
Specifies the value of the plane for which the isoline is to be calculated. Permitted data structures are scalar value und data series. All numeric data types are permitted. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||
Result |
Determines the result of the function. The argument Result can have the following values:
If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. If this argument is omitted, it will be set to the default value ISOLINE_2D. |
Remarks
An isoline is formed by the cut of a horizontal plane and of the surface specified by the data. The result is either a signal or a space curve, depending on the Result parameter. If a data series is specified for the Level parameter, multiple isolines are calculated and returned as a list. The isoline for a particular plane may consist of multiple, partially closed curves. These curves are then separated in the result by a void value. For best presentation, disable the option Bridge void values for the diagram curve.
Available in
FlexPro Basic, Professional, Developer Suite
Examples
Isoline(Surface, 100)
Returns the isoline for the level 100 as a signal.
Isoline(Surface, 100, ISOLINE_3D)
Returns the isoline for the level 100 as a space curve.
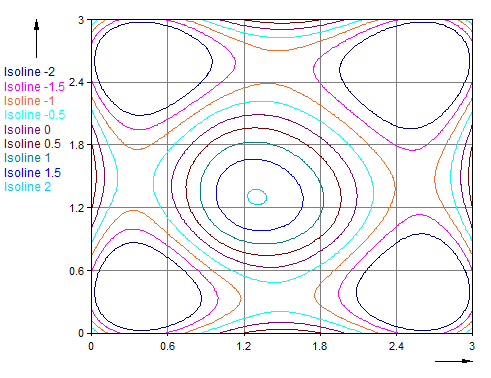
Dim Surface = {{0, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, -1, 0}, {0, 0, 0, 0}}
Surface = Spline2D(Surface, 100, 100, SPLINE_EQUIDISTANT + SPLINE_1DERIVATIVE, -10, 10, -10, 10)
Isoline(Surface, Series(-2, 2, 0.5))
The resolution of the isoline corresponds to the resolution of the passed matrix. You should therefore carry out interpolation beforehand if there are only a few grid points. This example interpolates the matrix through a grid of spline curves and then calculates the resulting isolines for the specified levels.
The following illustration shows the result: