RevolutionSyncSampling (FPScript)
Transformiert ein über der Zeit abgetastetes Signal in den Umdrehungsbereich, d.h. das Zeitsignal wird durch Umabtastung in einen äqudistant-abgetasteten Drehzahlbereich überführt. Effektives Verfahren zur Durchführung einer Ordnungsanalyse, da das Frequenzspektrum des in den Umdrehungsbereich konvertierten Signals direkt das Ordnungsspektrum liefert. Genauso können durch gewöhnliche Bandpassfilterung im Umdrehungsbereich unmittelbar die (zeitlichen) Ordnungsverläufe berechnet werden.
Syntax
RevolutionSyncSampling(Signal, Speed, [ SamplesPerRevolution = 0 ], [ SamplesPerRevolutionLimit = 256 ], [ ResampleMethod = REVSYNCSAMPLING_RESAMPLE_LINEAR ], [ ResampleFactor = 2 ] [ , OutputOptions = REVSYNCSAMPLING_OUTPUT_SIGNAL ])
Die Syntax der RevolutionSyncSampling-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Signal |
Das über der Zeit abgetastete Signal, welches in den äquidistanten Umdrehungsbereich transformiert werden soll. Die Einheit der X-Komponente muss zur Einheit Sekunden kompatibel sein (bei eingeschalteter Einheitenüberwachung). Ist keine Einheit der X-Komponente angegeben oder die Einheitenüberwachung ausgeschaltet, so wird die Einheit stets in Sekunden interpretiert. Erlaubte Datenstrukturen sind Signal. Es sind alle reellen Datentypen erlaubt außer Wahrheitswert, Kalenderzeit und Zeitspanne. Ungültige Werte sind in diesem Argument nicht zulässig. Für die X-Komponente gelten zusätzliche Beschränkungen.Die Werte müssen monoton wachsend sein. Ungültige Werte sind in diesem Argument nicht zulässig. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||
Speed |
Das über der Zeit abgetastete Drehzahlsignal, aus welchem der Umdrehungsbereich abgeleitet wird. Die Einheit der Y-Komponente muss zur Einheit 1/min (bzw. zu RPM = Umdrehungen pro Minute) kompatibel sein (bei eingeschalteter Einheitenüberwachung). Ist keine Einheit der Y-Komponente angegeben oder die Einheitenüberwachung ausgeschaltet, so wird die Einheit stets als 1/min interpretiert. Die Einheit der X-Komponente muss zur Einheit Sekunden kompatibel sein (bei eingeschalteter Einheitenüberwachung). Ist keine Einheit der X-Komponente angegeben oder die Einheitenüberwachung ausgeschaltet, so wird die Einheit stets in Sekunden interpretiert. Die Abtastrate muss nicht notwendigerweise mit der Abtastrate von Signal übereinstimmen. Handelt es sich um einen Einzelwert, dann wird angenommen, dass das zu transformierende Signal bei konstanter Drehzahl aufgezeichnet wurde. Erlaubte Datenstrukturen sind Einzelwert und Signal. Es sind alle reellen Datentypen erlaubt außer Wahrheitswert, Kalenderzeit und Zeitspanne. Das Argument wird auf die Einheit min^-1 transformiert. Ungültige Werte sind in diesem Argument nicht zulässig. Für die X-Komponente gelten zusätzliche Beschränkungen.Die Werte müssen monoton wachsend sein. Ungültige Werte sind in diesem Argument nicht zulässig. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||
SamplesPerRevolution |
Bestimmt die Abtastung des in den Umdrehungsbereich transformierten Signals (Anzahl Datenpunkte pro Umdrehung). Die Hälfte des Wertes bestimmt die maximale Ordnung, die nach dem Abtasttheorem durch Fourier-Analyse überhaupt berechnet werden kann. Es sollte ein Wert eingestellt werden, so dass oberhalb der Hälfte des Werts alle weiteren Ordnungen vernachlässigbar klein sind. Ansonsten entstehen Alias-Effekte (gemäß Abtasttheorem). Der Vorgabewert 0 wählt einen automatischen Wert, so dass die theoretisch größte im Signal vorkommende Ordnung mittels Fourier-Analyse im Ordnungsspektrum noch berechnet werden kann. Um die resultierende Datensatzgröße zu begrenzen, wird der automatisch berechnete Wert limitiert durch SamplesPerRevolutionLimit. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 0 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 0 gesetzt. |
||||||||||
SamplesPerRevolutionLimit |
Oberes Limit für die automatische Berechnung von SamplesPerRevolution. Es sollte ein Wert eingestellt werden, so dass oberhalb der Hälfte des Werts alle weiteren Ordnungen vernachlässigbar klein sind. Ansonsten entstehen Alias-Effekte (gemäß Abtasttheorem). Das Argument bleibt unberücksichtigt, wenn SamplesPerRevolution nicht automatisch berechnet wird, d.h. wenn für SamplesPerRevolution ein Wert größer als 0 gewählt wurde. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer 0 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 256 gesetzt. |
||||||||||
ResampleMethod |
Gibt das Resampling-Verfahren an, mit dem das Zeitsignal vor Überführung in den Umdrehungsbereich an den (nicht-äquidistanten) Zeitpunkten der äquidistanten Umdrehungsstützstellen ausgewertet wird. Das Argument ResampleMethod kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert REVSYNCSAMPLING_RESAMPLE_LINEAR gesetzt. |
||||||||||
ResampleFactor |
Gibt den Faktor an, um den die Abtastrate des Zeitsignals für die Resampling-Verfahren REVSYNCSAMPLING_RESAMPLE_SPLINE und REVSYNCSAMPLING_RESAMPLE_FFT erhöht wird. Das Argument bleibt unberücksichtigt, wenn als Resampling-Verfahren REVSYNCSAMPLING_RESAMPLE_LINEAR gewählt wurde. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 2 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 2 gesetzt. |
||||||||||
OutputOptions |
Gibt an, welche Ergebnisse zurückgegeben werden sollen. Mehrere Ergebnisse werden als Liste ausgegeben. Wenn z. B. das in den Umdrehungsbereich transformierte Signal sowie die zu den Umdrehungsstützstellen berechneten Zeitpunkte ausgegeben werden sollen, so muss das Argument den Wert REVSYNCSAMPLING_OUTPUT_SIGNAL + REVSYNCSAMPLING_OUTPUT_TIME enthalten. Das Argument OutputOptions kann folgende Werte haben:
Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert REVSYNCSAMPLING_OUTPUT_SIGNAL gesetzt. |
Anmerkungen
Der Algorithmus des Transformationsverfahrens lässt sich schematisch wie folgt beschrieben:
In der Literatur wird das Verfahren auch als Synchronous Angular Sampling, Computed Order Tracking, Synchronous Sampling oder auch Adaptive Resampling bezeichnet, siehe [1], [2], [3], [4], [5] und [6]. Es handelt sich um ein effektives Verfahren zur Durchführung einer Ordnungsanalyse, da das gewöhnliche (Zeit-)Frequenzspektrum des in den Umdrehungsbereich konvertierten Signals nun direkt das Ordnungsspektrum liefert:
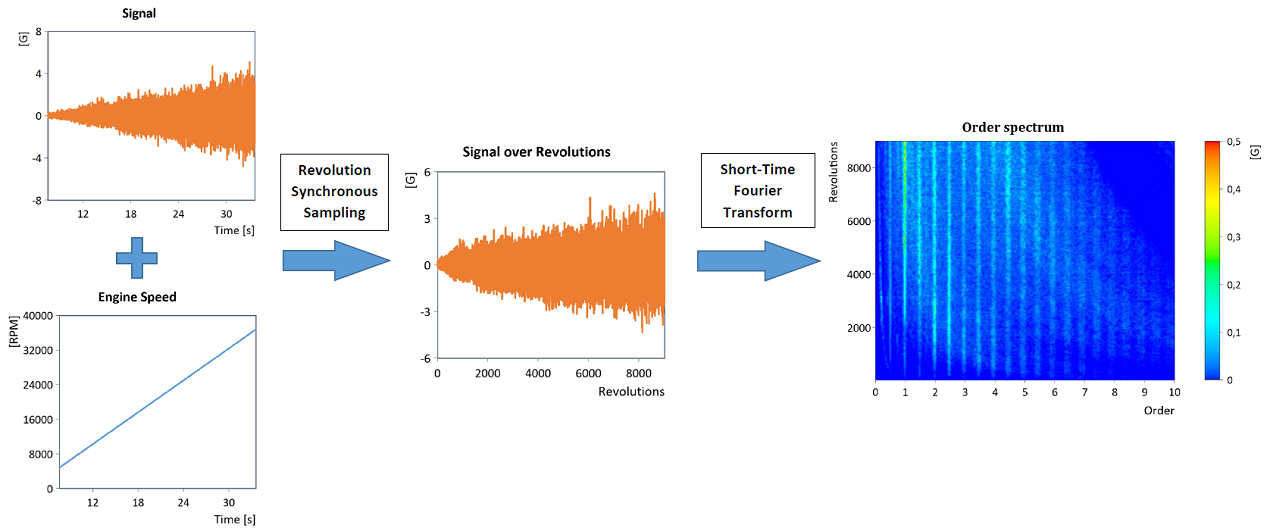
Genauso lässt sich durch gewöhnliche Bandpassfilterung (z.B. mit Hilfe eines geeigneten IIR-Bandpassfilter) im Umdrehungsbereich direkt der Verlauf einzelner Ordnungen ermitteln (hier abgebildet der blockweise RMS-Verlauf der gefilterten Ordnungen):
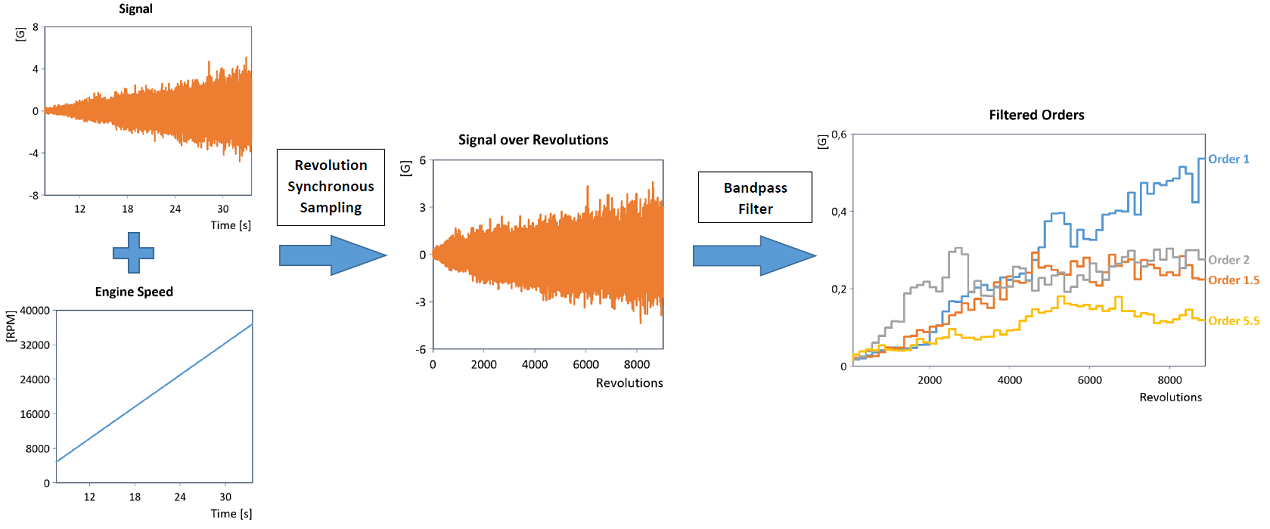
Bemerkung: Die Ordnungsanalyse mittels revolution synchronous resampling ist sehr flexibel und lässt sich auch für verrauschte sowie nicht-monotone Drehzahldatensätze durchführen.
Auf die Ergebnisse kann mit folgenden Listenelementnamen zugegriffen werden:
Konstante |
Bedeutung |
|---|---|
.["Signal_over_Revolutions"] |
Das in den Umdrehungsbereich transformierte Signal. |
.["Speed_over_Revolutions"] |
Das in den Umdrehungsbereich transformierte Drehzahlsignal. |
.["Time_over_Revolutions"] |
Die zu den Umdrehungsstützstellen zugehörigen (nicht-äquidistanten) Zeitpunkte. |
Sie können auch stets die Syntax Formelname.Listenelementname verwenden.
Hinweis Gemäß Abtasttheorem können theoretisch alle Ordnungen bis orderMax = 0.5*SamplingRate(Signal)/Maximum(Speed) detektiert und analysiert werden. Falls also SamplesPerRevolution automatisch berechnet wird, so wird dieser Wert auf einen Wert größer als dem Doppelten von orderMax gesetzt. Das gewährleistet, dass tatsächlich alle Ordnungen bis orderMax mittels Fourier-Analyse im Ordnungsspektrum berechnet und damit Alias-Effekte möglichst vermieden werden können.
Verfügbarkeit
Option Ordnungsanalyse
Beispiele
RevolutionSyncSampling(Signal, Speed)
Transformiert ein zeitbasiertes Signal in den Umdrehungsbereich.
Dim samplesPerRevolution = 64
Dim sigOverRev = RevolutionSyncSampling(Signal, Speed, samplesPerRevolution)
STFTSpectrum(sigOverRev, SPECTRUM_RMSAMPLITUDE,,, 8*samplesPerRevolution,,, 0)
Berechnet das Ordnungsspektrum des Drehzahl-synchron abgetasteteten Signals mit Hilfe des Zeit-Frequenzspektrums (STFTSpectrum-Funktion). Das Ordnungsspektrum wird bis zur Ordnung 32 (= samplesPerRevolution/2) berechnet und besitzt eine Ordnungsauflösung von 1/8. Bemerkung: Falls im ursprünglichen Signal betragsmäßig relevante Ordnungen größer als 32 vorhanden waren, so verfälschen diese das Ordnungsspektrum. Alias-Effekte sind die Folge.
Dim sigOverRev = RevolutionSyncSampling(Signal, Speed, 0, 256)
STFTSpectrum(sigOverRev, SPECTRUM_RMSAMPLITUDE,,, 16*SamplingRate(sigOverRev),,, 0)
Berechnet das Ordnungsspektrum des Drehzahl-synchron abgetasteten Signals mit Ordnungsauflösung von 1/16. Die Anzahl der Datenpunkte pro Umdrehung wird hierbei automatisch berechnet (ist aber begrenzt durch 256). Die theoretisch größte im Signal vorkommende Ordnung kann daher bei der anschließenden Fourier-Analyse noch berechnet werden.
Dim samplesPerRevolution = 64
Dim sigOverRev = RevolutionSyncSampling(Signal, Speed, samplesPerRevolution)
Dim coeff = IIRPeakFilter(3, 0.5, samplesPerRevolution) // order = 3, bandwidth = 0.5
Dim filteredOrder = Filter(sigOverRev, coeff, TRUE)
Sample(filteredOrder, Signal.X)
Berechnet den Zeitverlauf der dritten Ordnung (z.B. für akustische Analysen). Die gefilterte, dritte Ordnung wird hierbei mit Hilfe eines gewöhnlichen IIR-Bandpassfilters im Umdrehungsbereich mit Bandmittenfrequenz 3 und (symmetrischer) Ordnungsbandbreite von 0.5 berechnet. Abschließend wird auf die Original Zeitbasis zurücktransformiert.
Dim samplesPerRevolution = 64
Dim sigOverRev = RevolutionSyncSampling(Signal, Speed, samplesPerRevolution)
Dim coeff = IIRPeakFilter(3, 0.5, samplesPerRevolution) // order = 3, bandwidth = 0.5
Dim filteredOrder = Filter(sigOverRev, coeff, TRUE)
XOffsetScale(Mean(filteredOrder, MEAN_SQUARE + CALC_BLOCK, 128 * samplesPerRevolution)[0,-2], 128/2.)
Berechnet den blockweisen RMS-Verlauf der dritten Ordnung des Drehzahl-synchron abgetasteten Signals (Blockgröße = 128 Umdrehungen). Die gefilterte, dritte Ordnung wird hierbei mit Hilfe eines gewöhnlichen IIR-Bandpassfilters im Umdrehungsbereich mit Bandmittenfrequenz 3 und (symmetrischer) Ordnungsbandbreite von 0.5 berechnet.
RevolutionSyncSampling(Signal, Speed,,,,, REVSYNCSAMPLING_OUTPUT_SIGNAL + REVSYNCSAMPLING_OUTPUT_TIME)
Es wird das in den Umdrehungsbereich transformierte Signal sowie die zu den Umdrehungen zugehörigen Zeitpunkte zurückgegeben.
Dim rev = ChangeUnit(Integral(Speed), "1") // Step 1
Dim rev_equid = (rev[-1]*128, 0, 1/128) // Step 2
Dim t_nonequid = Sample(rev.X, rev.Y, rev_equid, true)
Dim sig = Sample(Signal, t_nonequid, true) // Step 3
Signal(sig, rev_equid)
Äquivalenter FPScript-Code zu RevolutionSyncResampling(Signal, Speed, 128,, REVSYNCSAMPLING_RESAMPLE_LINEAR).
Dim rev = ChangeUnit(Integral(Speed), "1") // Step 1
Dim rev_equid = (rev[-1]*128, 0, 1/128) // Step 2
Dim t_nonequid = Sample(rev.X, rev.Y, rev_equid, true)
Dim sig = Sample(Resample(Signal, 4, RESAMPLE_FFT), t_nonequid, true) // Step 3
Signal(sig, rev_equid)
Äquivalenter FPScript-Code zu RevolutionSyncResampling(Signal, Speed, 128,, REVSYNCSAMPLING_RESAMPLE_FFT, 4).
Siehe auch
HarmonicRemovalFilter-Funktion
Analyseobjekt Umdrehungssynchrone Abtastung
Analyseobjekt Umdrehungssynchrone Ordnungsanalyse
Analyseobjekt Zeit-Frequenz Spektralanalyse
Literatur
[1] K. R. Fyfe, E. D. S. Munck: Analysis of computed order tracking. In: Mechanical Systems and Signal Processing, Vol. 11, Issue 2, Pages 187-205. 1997.
[2] Jürgen Helmut Funck: Synchronous data acquisition with wireless sensor networks. In: Chichester, UK: John Wiley and Sons. 2011.
[3] Bonnardot, F. et al.: Use of the acceleration signal of a gearbox in order to perform angular resampling (with limited speed fluctuation). In: Mechanical Systems and Signal Processing, Vol. 19, Isuue 4, Pages 766–785. 2005.
[4] J. Blough: Adaptive Resampling - Transforming from the time to the Angle domain. In: 24th Conference and Exposition on Structural Dynamics, IMAC-XXIV. 2006.
[5] J. Blough: A survey of DSP methods for rotating machinery analysis, what is needed, what is available. In: Journal of Sound and Vibration, Vol. 262, Issue 3, Pages 707-720. 2003.
[6] A. Brandt: Noise and Vibration Analysis: Signal Analysis and Experimental Procedures. In: John Wiley and Sons, Ltd., Chichester. 2011.