HarmonicRemovalFilter (FPScript)
Entfernt harmonische Komponenten aus Zeitsignalen (Oberwellenentfernung). Hierzu werden die Daten vom Zeitbereich in den Umdrehungsbereich konvertiert, wo eine Zyklus-Mittelung und -Subtraktion die gewünschte Oberwellenentfernung liefert.
Syntax
HarmonicRemovalFilter(Signal, SpeedOrFundamentalFrequency, [ OrderForHarmonicRemoval = 1 ], [ NumberOfCyclesForAveraging = 15 ], [ SamplesPerRevolution = 512 ] [ , OutputOptions = HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_TIME_DOMAIN ])
Die Syntax der HarmonicRemovalFilter-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Signal |
Das über der Zeit abgetastete Signal, aus welchem harmonische Komponenten (Oberwellen) entfernt werden sollen. Die Einheit der X-Komponente muss zur Einheit Sekunden kompatibel sein (bei eingeschalteter Einheitenüberwachung). Ist keine Einheit der X-Komponente angegeben oder die Einheitenüberwachung ausgeschaltet, so wird die Einheit stets in Sekunden interpretiert. Erlaubte Datenstrukturen sind Signal. Es sind alle reellen Datentypen erlaubt außer Wahrheitswert, Kalenderzeit und Zeitspanne. Ungültige Werte sind in diesem Argument nicht zulässig. Für die X-Komponente gelten zusätzliche Beschränkungen.Die Werte müssen monoton wachsend sein. Ungültige Werte sind in diesem Argument nicht zulässig. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||
SpeedOrFundamentalFrequency |
Die für die Oberwellenentfernung zugrundeliegende rotierende Komponente als ein über der Zeit abgetastetes Drehzahlsignal (aus welchem der Umdrehungsbereich für die Oberwellenentfernung abgeleitet wird). Alternativ die zugrundeliegende feste Grundfrequenz. Die Einheit der Y-Komponente muss zur Einheit 1/min (bzw. zu RPM = Umdrehungen pro Minute) kompatibel sein (bei eingeschalteter Einheitenüberwachung). Ist keine Einheit der Y-Komponente angegeben oder die Einheitenüberwachung ausgeschaltet, so wird die Einheit stets als 1/min interpretiert. Die Einheit der X-Komponente muss zur Einheit Sekunden kompatibel sein (bei eingeschalteter Einheitenüberwachung). Ist keine Einheit der X-Komponente angegeben oder die Einheitenüberwachung ausgeschaltet, so wird die Einheit stets in Sekunden interpretiert. Die Abtastrate muss nicht notwendigerweise mit der Abtastrate von Signal übereinstimmen. Handelt es sich um einen Einzelwert, dann wird angenommen, dass das zu filternde Signal bei dieser konstanten Drehzahl aufgezeichnet wurde bzw. dass harmonische Komponenten bezogen auf Vielfachen dieser festen Grundfrequenz entnommen werden sollen. Erlaubte Datenstrukturen sind Einzelwert und Signal. Es sind alle reellen Datentypen erlaubt außer Wahrheitswert, Kalenderzeit und Zeitspanne. Das Argument wird auf die Einheit min^-1 transformiert. Ungültige Werte sind in diesem Argument nicht zulässig. Für die X-Komponente gelten zusätzliche Beschränkungen.Die Werte müssen monoton wachsend sein. Ungültige Werte sind in diesem Argument nicht zulässig. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||
OrderForHarmonicRemoval |
Definiert die Ordnung (d.h. Vielfache der Drehzahl bzw. Vielfache der Grundfrequenz), die mitsamt aller harmonischen Komponenten aus dem Zeitsignal entfernt werden soll. Die Wahl von 4 bedeutet beispielsweise, dass Ordnungen 4, 8, 12, 16, 20 usw. entfernt werden. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle numerischen Datentypen erlaubt. Der Wert muss größer 0 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 1 gesetzt. |
||||||||||
NumberOfCyclesForAveraging |
Für die Oberwellenentfernung wird das zu filternde Signal zuerst in den Umdrehungsbereich transformiert, wo eine gleitende Zyklenmittelung und -subtraktion durchgeführt wird. Dieser Wert bestimmt die Anzahl der zu mittelnden Zyklen im Umdrehungsbereich zur Berechnung der jeweiligen gemittelten harmonischen Ordnung. Je größer der Wert, desto größer die Filterselektivität. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 2 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 15 gesetzt. |
||||||||||
SamplesPerRevolution |
Für die Oberwellenentfernung wird das zu filternde Signal zuerst in den Umdrehungsbereich transformiert. Dieser Wert bestimmt die Abtastung des in den Umdrehungsbereich transformierten Signals (Anzahl Datenpunkte pro Umdrehung). Die Hälfte des Wertes bestimmt die maximale Ordnung, die nach dem Abtasttheorem durch Fourier-Analyse überhaupt berechnet werden kann. Es sollte also ein Wert eingestellt werden, so dass oberhalb der Hälfte des Werts alle weiteren Ordnungen vernachlässigbar klein sind. Ansonsten entstehen Alias-Effekte (gemäß Abtasttheorem). Kleinere Werte hingegen verringern die Berechnungszeit des Algorithmus. Der Wert muss außerdem so eingestellt werden, dass SamplesPerRevolution / OrderForHarmonicRemoval ganzzahlig ist. Falls die letztgenannte Bedingung nicht erfüllt ist, so werden automatisch approximierte Werte für die Anzahl an Datenpunkten pro Umdrehung und die zu filternde Ordnung berechnet, welche diese Bedingung erfüllen. Der vom Algorithmus berechnete, approximierte Wert für die zu filternde Ordnung stimmt dann bis auf mindestens 2 Nachkommstellen mit OrderForHarmonicRemoval überein. Der vom Algorithmus berechnete, approximierte Wert für die Anzahl an Datenpunkten pro Umdrehung ist in diesem Fall nach unten begrenzt durch den Wert von SamplesPerRevolution. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 1 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 512 gesetzt. |
||||||||||
OutputOptions |
Gibt an, welche Ergebnisse zurückgegeben werden sollen. Mehrere Ergebnisse werden als Liste ausgegeben. Wenn z. B. das im Umdrehungsbereich gefilterte Signal (ohne Oberwellen) sowie das in den Zeitbereich zurücktransformierte gefilterte Zeitsignal ausgegeben werden sollen, so muss das Argument den Wert HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_REVOLUTION_DOMAIN + HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_TIME_DOMAIN enthalten. Das Argument OutputOptions kann folgende Werte haben:
Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_TIME_DOMAIN gesetzt. |
Anmerkungen
Der Algorithmus des Transformationsverfahrens lässt sich schematisch wie folgt beschrieben (siehe z.B. [1], [2] oder [3]):
1) Transformation in den Umdrehungsbereich: Zuerst wird Signal vom Zeitbereich in den Umdrehungsbereich transformiert (analog dem Verfahren der RevolutionSyncSampling-Funktion, wobei hier eine lineare Transformation gewählt wird). Der Umdrehungsbereich wird hierbei insbesondere aus dem Argument SpeedOrFundamentalFrequency berechnet. Außerdem sind für die Transformation die für die RevolutionSyncSampling-Funktion notwendigen Argumente bzgl. Anzahl an Datenpunkten pro Umdrehung erforderlich.
2) Zyklus-Mittelung: Im Umdrehungsbereich erfolgt eine (gleitende) Mittelwertbildung über eine benutzerdefinierte Anzahl von Zyklen. Alles was sich synchron mit der Welle dreht, ist eine Harmonische, die in diesen Mittelwertzyklus einbezogen wird. Komponenten, die nicht-synchron mit der Welle erster Ordnung drehen, werden herausgemittelt. Der Mittelwertzyklus besteht daher aus Daten, die mit dem zugrundeliegenden Tachometer (d.h. mit SpeedOrFundamentalFrequency) synchron und harmonisch sind. In einem Viertaktmotor gibt es beispielsweise ein Verbrennungsereignis pro zwei Umdrehungen der Kurbelwelle. Ein Zyklus besteht also aus 2 Umdrehungen. Will man hier also das Verbrennungsereignis inklusive den harmonischen Komponenten entfernen, so muss OrderForHarmonicRemoval auf den Wert 0.5 gesetzt werden.
3) Zyklus-Subtraktion: Der (gleitende) Mittelwertzyklus wird dann von jedem einzelnen Zyklus subtrahiert, um die gewünschte Oberwellenentfernung durchzuführen. Man erhält dann das im Umdrehungsbereich gefilterte Signal (ohne Oberwellen der herausgefilterten Ordnung).
4) Rücktransformation in den Zeitbereich: Abschließend wird das im Umdrehungsbereich gefilterte Signal zurück in den Zeitbereich transformiert.
Als Beispiel betrachte man das von einem Hochlauf berechnete Ordnungsspektrum eines Zeitsignals:
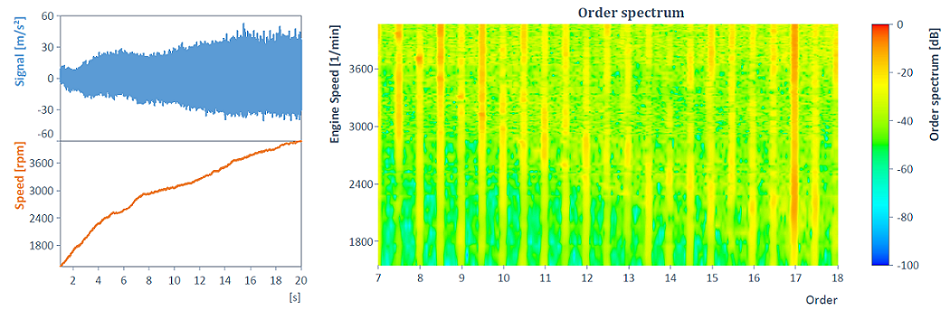
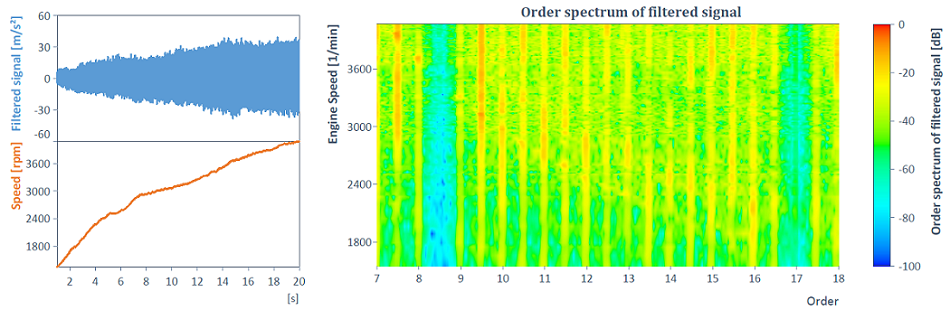
Mit Hilfe der zugrundeliegenden HarmonicRemovalFilter-Funktion lässt sich beispielsweise Ordnung 8.5 mitsamt aller harmonischen Komponenten entfernen:
Falls das Ergebnis eine Liste ist, so kann auf die Ergebnisse mit folgenden Listenelementnamen zugegriffen werden:
Konstante |
Bedeutung |
|---|---|
.["Signal_over_Time"] |
Das in den Original-Zeitbereich zurücktransformierte, gefilterte Signal (ohne Oberwellen). |
.["Signal_over_Revolutions"] |
Das in den Umdrehungsbereich transformierte, gefilterte Signal (ohne Oberwellen). |
.["Speed_over_Revolutions"] |
Das in den Umdrehungsbereich transformierte Drehzahlsignal. |
.["Time_over_Revolutions"] |
Die zu den Umdrehungsstützstellen zugehörigen (nicht-äquidistanten) Zeitpunkte. |
Sie können auch stets die Syntax Formelname.Listenelementname verwenden.
Hinweis Gemäß Abtasttheorem können theoretisch alle Ordnungen bis orderMax = 0.5*SamplingRate(Signal)/Maximum(Speed) detektiert und analysiert werden. SamplesPerRevolution sollte also auf einen Wert größer als dem Doppelten von orderMax gesetzt werden.
Verfügbarkeit
Option Ordnungsanalyse
Beispiele
HarmonicRemovalFilter(Signal, Speed, 8.5)
Entfernt die 8.5te Ordnung (bezogen auf das Drehzahlsignal) mitsamt aller harmonischen Komponenten. Als Ergebnis erhält man das im Zeitbereich gefilterte Signal (ohne die entsprechenden Oberwellen)
HarmonicRemovalFilter(Signal, 12 Hz, 1)
Entfernt in einem Signal die 12 Hz Grundfrequenz und deren harmonische Komponenten. Als Ergebnis erhält man das im Zeitbereich gefilterte Signal.
Dim SyncSampling = RevolutionSyncSampling(Signal, Speed, 512,,,,REVSYNCSAMPLING_OUTPUT_ALL) // Step 1: transform to rev. domain
Dim n = 512/4
Dim cycles = Reshape(SyncSampling.["Signal_over_Revolutions"], {NumberOfRows(SyncSampling.["Signal_over_Revolutions"])/n, n})
Dim avgeragedCycles = Mean(cycles, MEAN_ARITHMETIC + PROCESS_ROWS + CALC_MOVING, 25) // Step 2: cycle averaging
Dim harmonicRemoval = Signal(Reshape(cycles - avgeragedCycles), SyncSampling.["Time_over_Revolutions"]) // Step 3: cycle substraction
RemoveVoidValues(Sample(harmonicRemoval, Signal.X)) // step 4: transform back to time domain
Äquivalenter FPScript-Code zu HarmonicRemovalFilter(Signal, Speed, 4, 25, 512).
Siehe auch
RevolutionSyncSampling-Funktion
Analyseobjekt Oberwellenenfilter
Analyseobjekt Umdrehungssynchrone Ordnungsanalyse
Analyseobjekt Umdrehungssynchrone Abtastung
Literatur
[1] B. Peeters, B. Cornelis, K. Janssens, H. Van der Auweraer: Removing disturbing harmonics in Operational Modal Analysis. In: Proceedings of the International Operational Modal Analysis Conference IOMAC, Copenhagen, Denmark. 2007.
[2] R.B. Randall: State of the art in monitoring rotating machinery. In: Proceedings of the International Seminar on Modal Analysis ISMA, Leuven, Belgium. 2002.
[3] E. Bechhoefer, M. Kingsley: A Review of Time Synchronous Average Algorithms. In: Proceedings of the Annual Conference of the Prognostics and Health Management Society, San Diego, USA. 2009.