Mit der nicht-linearen Kurvenanpassung ist es möglich, eine Modellfunktion in Abhängigkeit von einer unabhängigen Variablen und von mehreren Parametern an einen vorgegebenen Datensatz anzunähern. Hauptanwendungsgebiet ist die Ermittlung der Modellparameter, so dass das gewählte Modell am besten an die Daten angepasst wird. Hierzu ist ein exaktes Wissen über das gewählte Modell und deren Parameter erforderlich. Die nicht-lineare Kurvenanpassung kann allerdings auch dazu verwendet werden, um einen vorgegebenen Datensatz zu interpolieren bzw. zu glätten. In diesem Fall ist es nicht entscheidend, welches Modell zur Analyse verwendet wird. Eine Prüfung der berechneten Modellparameter entfällt ebenfalls. Für dieses Anwendungsgebiet ist ein Werkzeug sinnvoll, das die zur Verfügung stehenden Modelle miteinander vergleicht (Modellbewertung).

Ein Beispiel

Ein Silberstück wird mit Wärmeneutronen bestrahlt, um die zwei kurzlebigen Silberisotope 47Ag108 und 47Ag110 zu erzeugen, die anschließend wieder durch Betaausstrahlungen zerfallen. Bei dem Experiment werden die ausgestrahlten Betateilchen in 15s-Intervallen für einen Zeitraum von 4 Minuten gezählt. Das Ergebnis ist eine abfallende Exponentialkurve, die durch die Modellfunktion Abklingende Exponentialfunktion (Variante 2) beschrieben wird. Parameter p0 entspricht der Hintergrundstrahlung und p1 und p3 entsprechen den Amplituden der beiden angeregten Zuständen mit den mittleren Lebensdauern p2 und p4. Da das Modell in den Parametern p2 und p4 nicht-linear ist, wird ein Verfahren zur nicht-linearen Kurvenanpassung benötigt.

Wählen Sie Datei > Projektdatenbank öffnen und öffnen Sie die Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Tutorials\Curve Fitting.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021>Examples>Tutorials>Curve Fitting.fpd. Öffnen Sie den Ordner Example Silver und öffnen Sie das 2D-Diagramm Ag-Diagram per Doppelklick.

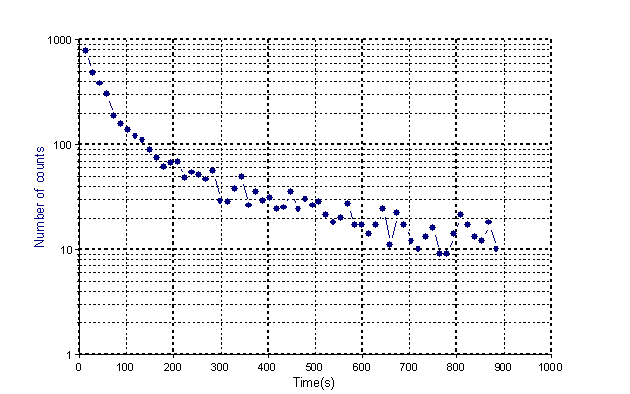
Es handelt sich um ein Diagramm für das Signal Ag mit 59 Fließkomma-Werten. (Quelle: Bevington, p.142ff)

Modellbewertung

Schließen Sie das Diagramm und markieren Sie den Datensatz Ag, das zu analysierende Signal des oben beschriebenen Experiments.

Klicken Sie auf Einfügen[Analysen] > Analyse-Assistent.

Wählen Sie die Kategorie Kurvenanpassung und darin Nicht-lineare Kurvenanpassung aus. Klicken Sie danach auf die Weiter-Schaltfläche. Klicken Sie auf Modellbewertung um das Modell, das sich am besten an den gewählten Datensatz annähern lässt, zu ermitteln.

Es öffnet sich ein Dialog, in dem Sie den Algorithmus, die maximale Anzahl Funktionsaufrufe und die Modellkategorien wählen können. Die Zuordnung der einzelnen Modellfunktionen zu den Kategorien finden Sie unter Modelle. Als Algorithmus wählen Sie Full-Newton. Stellen Sie die maximalen Funktionsaufrufe auf 300 und markieren Sie alle Kategorien. Je größer Sie den Wert Maximalanzahl Funktionsaufrufe wählen, desto mehr Modelle liefern ein Ergebnis. Allerdings verlängert sich dadurch auch die Berechnungszeit des Algorithmus. Klicken Sie auf Weiter.

Jetzt wird eine nicht-lineare Kurvenanpassung für alle gewählten Modelle durchgeführt und die Modelle anhand der absoluten Quadratsumme der Residuen SSE sortiert und aufgelistet. In der Liste können Sie das Modell, das Sie weiter verwenden möchten, auswählen. Außerdem wird das ermittelte Bestimmtheitsmaß R2 aufgelistet. R2 = 1,0 bedeutet, dass die Kurve durch jeden Datenpunkt geht. Mit einem bekannten X-Wert lässt sich der dazugehörige Y-Wert exakt bestimmen. R2 = 0,0 bedeutet, dass das Regressionsmodell die Daten nicht besser als eine horizontale Linie durch den Mittelwert der Daten beschreibt. Bekannte X-Werte helfen nicht, den dazugehörigen Y-Wert zu berechnen.

Wählen Sie das Modell mit der kleinsten absoluten Quadratsumme der Residuen, das Modell NIST-Modell Hahn1, um eine bestmögliche Annäherung zu erzielen. Schließen sie nun das Dialogfeld Modellbewertung, indem sie auf Fertigstellen klicken. Klicken zweimal auf Weiter. Aktivieren Sie die Option Diagramme und Tabellen, die das Ergebnis darstellen. Klicken Sie anschließend auf Fertigstellen.

Öffnen Sie das neu erstellte Diagramm Signal, um sich das Ergebnis der Signalglättung anzusehen. Folgendes Diagramm zeigt das Ergebnis in logarithmischer Skalierung.

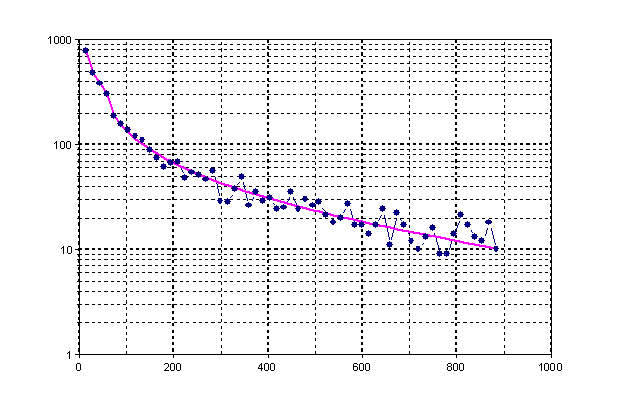
Lineare Approximation

Bevor nun die Modellparameter mit der nicht-linearen Kurvenanpassung bestimmt werden, wird das zu analysierende Signal zerlegt und so transformiert, dass eine lineare Approximation zur Bestimmung der Modellparameter verwendet werden kann. Diese Methode kann dazu verwendet werden, die Startparameter zu berechnen. In vielen Fällen ist die Wahl der Startparameter ein entscheidendes Kriterium für die erfolgreiche Berechnung der Modellparameter mit Hilfe der nicht-linearen Kurvenanpassung. Das Ergebnis der Linearisierung dient in diesem Fall zur Überprüfung des Ergebnisses der nicht-linearen Kurvenanpassung.

Die zu untersuchende Modellfunktion Abklingende Exponentialfunktion (Variante 2) hat die Form:

Zuerst die Hintergrundstrahlung (Parameter p0) ermittelt. Für eine grobe Schätzung genügt ein Blick auf die Signalkurve. Die Exponentialkurve nähert sich dem zu bestimmenden Offset. Zur groben Schätzung der Hintergrundstrahlung werden die letzten drei Signalwerte gemittelt. Dies ergibt den Wert 13,3. Zur Bestimmung der weiteren Parameter wird der Offset von jedem Punkt des Eingangsignals subtrahiert. Das berechnete Signal wird in zwei Teilbereiche A (x < 120) und B (x > 200) zerlegt. Die Parameter p3 und p4 werden nun durch eine logarithmische Transformation und eine lineare Approximation genähert.

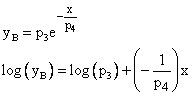
Anhand dieses Ergebnisses kann die langlebige Komponente ermittelt werden. Nun wird dieser Anteil vom Bereich A subtrahiert, um die kurzlebige Komponente ermitteln zu können. Auch hier erfolgt eine logarithmische Transformation und eine lineare Approximation.

Die ermittelten Parameter lauten:

Öffnen Sie die Formel Linearization im Ordner Example Silver, um sich die FPScript-Funktion dieser Berechnung anzusehen.

Parameter schätzen

Nach dieser groben Parameterschätzung können Sie mit der exakten Bestimmung der Modellparameter beginnen.

Dazu markieren Sie das Signal Ag.

Wählen Sie Einfügen[Analysen] > Analyse-Assistent.

Wählen Sie die Kategorie Kurvenanpassung und darin Nicht-lineare Kurvenanpassung aus. Klicken Sie danach auf Weiter. Wählen Sie das Modell Abklingende Exponentialfunktion (Variante 2). Außerdem können Sie sich ein Vorhersageband (95%, 99% bzw. 99,9%) und ein Konfidenzband (95%, 99% bzw. 99,9%) anzeigen lassen. Das Konfidenzband ist nützlich für sich wiederholende Daten, d. h. für jeden X-Wert gibt es mehrere Y-Werte bzw. es gibt einen Y-Wert, der den Mittelwert mehrerer Messpunkte repräsentiert. Ein 95% Konfidenzintervall ist der Y-Bereich für einen gegebenen X-Wert, der mit 95% Wahrscheinlichkeit den wahren Y-Wert enthält. Das Vorhersageband macht eine Aussage über die Streuung der zu analysierenden Daten. Würden Sie mehr Datenpunkte sammeln, so würden 95% der Punkte in den Bereich des Vorhersagebandes fallen.

Nachdem Sie das Modell gewählt haben, sehen Sie direkt das Ergebnis der nicht-linearen Kurvenanpassung im Vorschaufenster des Assistenten. Im ersten Diagramm wird das Eingangssignal und das geschätzte Signal dargestellt. In einem weiteren Diagramm werden die Residuen angezeigt. In den beiden Tabellen finden Sie die geschätzten Parameter und eine Reihe statistischer Werte zur Ergebnisanalyse. Die berechneten Modellparameter haben die Werte:

p1 und p2 sind in diesem Fall die Parameter der langlebigen Komponente, p3 und p4 die Parameter der kurzlebigen Komponente.

Klicken Sie danach auf Weiter. Auf dieser Seite des Assistenten kann durch diverse Einstellmöglichkeiten die Berechnung beeinflusst werden. Es lässt sich ein Algorithmus auswählen. Zudem können diverse Gewichtungsmodi und Skalierungsmodi verwendet werden.

Die wichtigste Einstellmöglichkeit dieser Seite ist die Liste Startwerte. Hier lassen sich die Startwerte der Modellparameter festlegen. Außerdem kann festgelegt werden, ob ein Parameter einen festen Wert hat oder nicht. Für den Full-Newton Algorithmus lassen sich zudem eine Unter- und eine Obergrenze angeben.

Entscheidend für das Berechnungsergebnis ist die Wahl der Startparameter. Liegt der gewählte Startpunkt weit entfernt vom globalen Minimum, so liefert der Algorithmus möglicherweise kein Ergebnis bzw. ein anderes lokales Minimum. Um die Wahrscheinlichkeit zu erhöhen, dass es bei dem angezeigten Ergebnis um ein globales Minimum handelt, sollte die Berechnung mit unterschiedlichen Startwerten durchgeführt werden. Für Modelle mit vier oder weniger Parametern steht die Option Startparameter schätzen zur Verfügung. Für jeden Parameter werden jeweils 10 zufallsverteilte Werte berechnet, die sich in dem durch die Untergrenze und Obergrenze festgelegten Bereich befinden. Nun wird für jede Kombination die absolute Quadratsumme der Residuen berechnet. Die Kombination mit der kleinsten Quadratsumme liefert die Startwerte. Die Parameterstartwerte können auch durch eine FPScript-Formel berechnet werden. Die Abbruchkriterien des Algorithmus kann durch die Einstellmöglichkeiten Maximalanzahl Funktionsaufrufe, X-Toleranz, Y-Toleranz, F-Toleranz und G-Toleranz beeinflusst werden. Die Berechnung der ersten Iteration hängt von der eingestellten Schrittgrenze ab.

Auf der letzten Seite des Assistenten wird festgelegt, welche Diagramme, Tabellen und Dokumente neben dem Analyseobjekt bei der Auswertung angelegt werden sollen. Wählen Sie die Option Diagramme und Tabellen, die das Ergebnis darstellen, um die im Vorschaufenster angezeigten Diagramme und Tabellen zu erzeugen. Wenn Sie sich die Kovarianzmatrix , die Korrelationsmatrix, den Standardfehler der Parameter und den Konfidenzbereich der Parameter in Tabellenform anzeigen lassen möchten, so wählen Sie zusätzlich die Option Zusätzliche tabellarische Auswertungen. Klicken Sie die Fertigstellen Schaltfläche, um den Assistenten zu beenden.

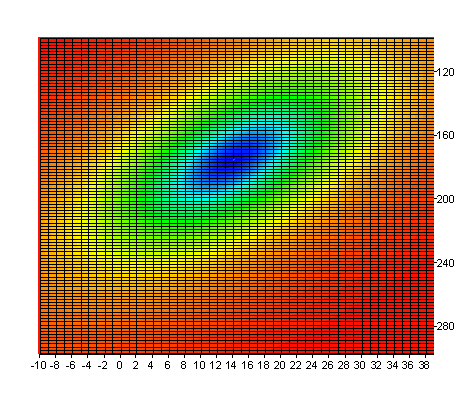
Um nun zu veranschaulichen, dass es sich bei dem Ergebnis um ein lokales Minimum handelt, wird in der Formel Surface die absolute Quadratsumme der Residuen für das Modell berechnet. Die Parameter p0 und p1 sind variabel, die Parameter p2, p3 und p4 sind fest. Das Ergebnis wird im Oberflächendiagramm Surface dargestellt. Es lässt sich gut erkennen, dass das Minimum bei p0 = 14 und p1 = 176  liegt.

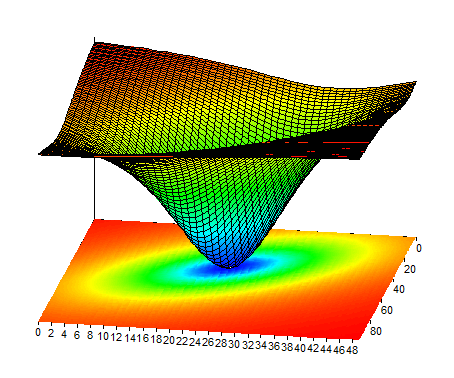
Startskript verwenden

Dieses Beispiel zeigt, wie ein Startskript dazu verwendet werden kann, um die Startwerte der Modellparameter zu berechnen.

Öffnen Sie dazu die oben beschriebene Formel Linearization, markieren Sie den Inhalt der Formel (STRG+A) und speichern ihn in die Zwischenablage (STRG+C). Markieren Sie das Signal Ag.

Öffnen Sie den Assistenten der Nicht-linearen Kurvenanpassung und gehen Sie auf die dritte Seite des Assistenten. Klicken Sie auf die Schaltfläche. Fügen Sie den Skriptcode aus der Zwischenablage in das Eingabefeld ein (STRG+V). Klicken Sie auf Berechnen, um das Skript zu überprüfen. Das Ergebnis ist eine Datenreihe mit 5 64-Bit Fließkomma-Werten. Klicken Sie auf Übernehmen, um die berechneten Werte als Startwerte zu übernehmen. Sollte die Anzahl der berechneten Werte nicht der Anzahl der Modellparameter entsprechen, so werden die berechneten Werte nicht übernommen. Statt den Skriptcode direkt einzufügen, könnten Sie auch auf eine bereits erstellte Formel verweisen, in dem Sie in das Eingabefeld den Namen der Formel eintragen. Dann ist allerdings der Code nur so lange gültig, wie das Formelobjekt existiert.

Benutzerdefiniertes Modell

Neben den vordefinierten Modellen ist es möglich, eigene Modellfunktionen zu definieren und benutzerabhängig abzuspeichern. Das folgende Beispiel zeigt, wie solch ein benutzerdefiniertes Modell angelegt wird. Wählen Sie Datei > Projektdatenbank öffnen und öffnen Sie die Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Tutorials\Curve Fitting.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021 >Examples>Tutorials>Curve Fitting.fpd. Öffnen Sie den Ordner Custom Model und öffnen Sie die Formel Data per Doppelklick. Die Formel berechnet ein Signal anhand der polynomialen Funktion y = p0 + p1x + p2x² + p3x³. Es handelt sich um ein Signal mit 1000 64-Bit Fließkomma-Werten.

Da diese Modellfunktion linear ist, lassen sich die Parameter mit der FPScript-Funktion Approximation berechnen (Formel Lineare Approximation).

Um die Parameter mit Hilfe der nicht-linearen Kurvenanpassung zu ermitteln, markieren Sie die Formel Data und wählen Einfügen[Analysen] > Analyse-Assistent. Wählen Sie die Kategorie Kurvenanpassung und darin Nicht-lineare Kurvenanpassung aus. Klicken Sie danach auf Weiter. Geben Sie im Listenfeld Modell den Namen Poly3 für ein benutzerdefiniertes Modell an. Es erscheinen zwei Eingabefelder, in denen die Formel für die Modellfunktion bzw. die Formel für die partiellen Ableitungen der Modellfunktion eingegeben werden können. Schreiben Sie p[0] + p[1] * x + p[2] * x^2 + p[3] * x^3 in das Eingabefeld der Funktion. p[0] bis p[3] bezeichnen die jeweiligen Modellparameter. Wählen Sie im Listenfeld Parameteranzahl den Wert 4 aus. Klicken Sie auf Modell Speichern, um das Modell unter dem angegebenen Namen abzuspeichern. Wird im Vorschaufenster eine Fehlermeldung statt des gewünschten Ergebnisses angezeigt, so müssen Sie auf der nächsten Seite des Assistenten die Maximalanzahl Funktionsaufrufe erhöhen. Klicken Sie danach auf Weiter. Wählen Sie 300 Funktionsaufrufe.

Klicken Sie auf die Zurück-Schaltfläche. Damit die partiellen Ableitungen nicht numerisch, sondern analytisch berechnet werden, müssen Sie die Formeln der partiellen Ableitungen im Eingabefeld Ableitungen eingeben: [ 1, x, x^2, x^3 ]. Die partiellen Ableitungen müssen als Liste übergeben werden. Das Ergebnis der geschätzten Modellparameter ist nun exakter. Außerdem verringert sich beim Algorithmus Full-Newton die benötigte Iterationsanzahl durch die analytische Berechnung der partiellen Ableitungen erheblich. Klicken Sie auf Modell Speichern, um das Modell erneut abzuspeichern.

Sie können den Parametern auch Namen zuweisen. Diese Namen werden dann in der Liste Startwerte auf der nächsten Seite des Assistenten angezeigt. Dazu müssen Sie die Formel, die die benutzerdefinierte Modellfunktion beschreibt, folgendermaßen ändern:

Dim p0 = p[0]
Dim p1 = p[1]
Dim p2 = p[2]
Dim p3 = p[3]
p0 + p1 * x + p2 * x^2 + p3 * x^3

Die Variable p0 wird der Variablen p[0] zugewiesen, die Variable p1 der Variablen p[1], usw.. Sie müssen darauf achten, dass die Zuweisungen untereinander stehen. Klicken Sie auf Weiter, um sich die Liste Startwerte mit den umbenannten Parametern anzusehen.

Klicken Sie auf Fertigstellen, um den Assistenten zu verlassen.

Literatur

•P.R. Bevington, D.K. Robinson. Data Reduction and Error Analysis for the Physical Sciences, 3rd Ed., McGraw-Hill, New York, 2003.

•G. A. F. Seber, C. J. Wild. Nonlinear Regression. Wiley, New York, 2003.

•Harvey Motulsky, Arthur Christopoulos. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. Oxford University Press, 2004.

Siehe auch

Analyseassistent

Analyseobjekt Nicht-lineare Kurvenanpassung

Statistische Ausgabeoptionen der Nicht-linearen Kurvenanpassung

Nicht-lineare Modelle