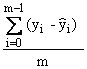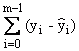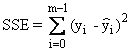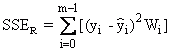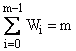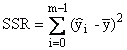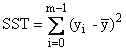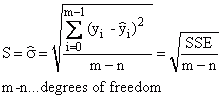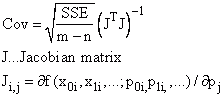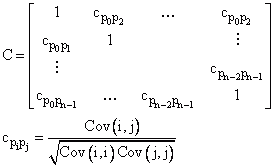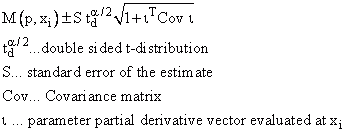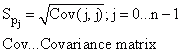Statistische Ausgabeoptionen der nicht-linearen Kurvenanpassung
Die Konvergenzkriterien allein reichen nicht aus, um das Ergebnis der nicht-linearen Kurvenanpassung beurteilen zu können. Daher steht eine Reihe statistischer Kenngrößen zur Verfügung, mit der man die Güte der Anpassung (Goodness-of-Fit) bestimmen kann.
Kenngröße |
Wird berechnet mit |
Bemerkung |
|---|---|---|
Schätzwerte / Die modellierten Daten |
|
Die Schätzwerte erhält man, indem man das ausgewählte Regressionsmodell mit den geschätzten Parametern p berechnet. |
Residuen |
|
Die Residuen sind die vertikale Differenz zwischen den eigentlichen Datenwerten und den jeweiligen Schätzwerten. Ist der Wert positiv, so liegt der jeweilige Punkt über der geschätzten Kurve. Ist der Wert 0, so liegt der Punkt auf der Kurve. |
Mittleres Residual |
|
Dies ist der Mittelwert der Residuen. |
Summe der Residuen |
|
Die Summe kann trotz vieler positiver und negativer Residuen 0 sein. |
Absolute Quadratsumme der Residuen |
|
|
Relative Quadratsumme der Residuen |
mit |
Diese Funktion wird oft auch als χ2-Funktion bezeichnet und ist ein Maß für die Güte der Anpassung. |
Regressionsquadratsumme |
|
|
Quadratsumme gesamt |
|
SST = SSE + SSR |
Fehler-Varianz |
|
|
Bestimmtheitsmaß R2 |
|
R2 = 1,0 bedeutet, dass die Kurve durch jeden Datenpunkt geht. Mit einem bekannten x-Wert lässt sich der dazugehörige y-Wert exakt bestimmen. R2 = 0,0 bedeutet, dass das Regressionsmodell die Daten nicht besser als eine horizontale Linie durch den Mittelwert der Daten beschreibt. Bekannte x-Werte helfen nicht, den dazu gehörigen y-Wert zu berechnen.
Eine alleinige Untersuchung des R2-Werts reicht nicht aus, um ein Modell zu interpretieren. Die beste Kurvenanpassung ist nutzlos, wenn die bestimmten Parameter physikalisch unsinnig sind oder das Konfidenzintervall zu breit ist.
|
Adjustiertes Bestimmtheitsmaß Ra2 |
|
Mit diesem Koeffizient kann man abwägen, ob es sich lohnt, die Anzahl der Parameter zu erhöhen, um ein größeres R2 zu erzielen. |
Kovarianzmatrix |
|
|
Korrelationsmatrix |
|
Wenn die Standardfehler groß sind und die Konfidenzintervalle breit sind, müssen weitere Nachforschungen betrieben werden. Eine Ursache kann eine Redundanz im ausgewählten Modell sein, d. h. mehrere Parameter des Modells korrelieren miteinander. Hier hilft die Korrelationsmatrix. Bei vollständig unkorrelierten Parametern kann man eine Verschlechterung der Kurvenanpassung, verursacht durch die Veränderung eines Parameters, nicht durch eine Anpassung eines anderen Parameters ausgleichen. Bei vollständig korrelierten Parametern ist dies möglich. Das bedeutet gleichzeitig, dass die Parameter nicht eindeutig bestimmt werden können. Beispiel: y = P0P1x |
Konfidenzstreifen |
|
Ausgegeben werden 95%, 99% und 99,9%. |
Prognosestreifen |
|
Ausgegeben werden 95%, 99% und 99,9%. |
Konfidenzbereich der Parameter |
ist das 100(1-alpha)% Konfidenzintervall für einen Parameter |
Es nicht richtig zu sagen, dass bei einem 90% Konfidenzintervall die Wahrscheinlichkeit, dass ein Parameter im Intervall liegt, 90% beträgt. Dies wäre nur der Fall, wenn man eine unendliche Anzahl an Datenpunkten zur Verfügung hätte. Anders ausgedrückt, wiederholt man ein Experiment unendlich mal, so enthalten 90% der Konfidenzintervalle den jeweiligen Parameter. Ausgegeben werden 95%, 99% und 99,9%. |
Standardfehler der Parameter |
|
|
Die Güte der Anpassung (Goodness-of-Fit)
•Konvergenzkriterien bei nicht-linearer Regression festlegen:
Nach jedem Iterationsschritt sollte die Funktion der kleinsten Fehlerquadrate (χ²-Funktion) geprüft werden. Die neu ermittelten Parameter werden mit dem bisher besten Ergebnis verglichen. Ist der neu berechnete Parameter besser, so wird dieser gespeichert.
•Residualstreuschaubild untersuchen:
Die Residuen sollten sich zufällig um 0 verteilen und keine erkennbaren Muster aufweisen. Vergrößern oder verkleinern sich die Residuen zum Beispiel mit der Zeit, so ist dies ein Zeichen dafür, dass ein anderes Modell besser ist bzw. eine Gewichtung erforderlich ist.
•Kurve des Regressionsmodells ansehen:
Die Datenwerte sollten zufällig über und unter der Kurve verteilt liegen.
•Prüfen Sie, wie gut das ausgewählte Modell die Daten beschreibt:
οR2 überprüfen:
R2 = 1,0 bedeutet, dass die Kurve durch jeden Datenpunkt geht.
R2 = 0,0 bedeutet, dass das Regressionsmodell die Daten nicht besser als eine horizontale Linie durch den Mittelwert der Daten beschreibt.
•Summe der Abweichungsquadrate:
Eine ideale Kurvenanpassung liefert das Ergebnis 0.
•Der Standardfehler der Schätzer ist die Standardabweichung der Differenzen zwischen den eingegebenen Daten und dem angepassten Modell. Dies gibt einen Einblick darüber, wie die Residuen um den Mittelwert verteilt sind. Eine ideale Kurvenanpassung würde den Wert 0 liefern.
•Prüfen Sie, ob die berechneten Werte überhaupt Sinn machen, d. h. z. B. keinen physikalischen Gesetzen widersprechen.
•Schauen Sie sich das Konfidenzintervall an.
Ist das Konfidenzintervall sehr breit, so ist die Kurvenanpassung nicht eindeutig. Andere Werte könnten zu einem ähnlichen Ergebnis führen.
•Es ist möglich, dass das falsche Minimum gefunden wurde. Dies ist der Fall, wenn es sich um ein lokales, aber nicht um das globale Minimum handelt. Daher ist es wichtig, gute Startwerte für das ausgewählte Modell zu finden.
Mehrere Untersuchungen mit unterschiedlichen Startwerten erhöhen die Sicherheit, dass es sich um die richtigen Ergebnisse handelt.
Literatur
•P.R. Bevington, D.K. Robinson. Data Reduction and Error Analysis for the Physical Sciences, 3nd Ed., McGraw-Hill, New York, 2003.
•J. Hartung. Statistik. Lehr- und Handbuch der angewandten Statistik. 9. Auflage. Oldenbourg Verlag, 1993.
•Harvey Motulsky, Arthur Christopoulos. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. Oxford University Press, 2004.
Siehe auch
Analyseobjekt Nicht-lineare Kurvenanpassung
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen