Dieses Tutorial behandelt sowohl den FIR-Filterentwurf als auch den IIR-Filterentwurf in FlexPro.

Beispielsignal

Wir erzeugen uns mit dem Analyseobjekt Signal ein synthetisches Signal, bei dem sich die Filtereigenschaften sehr gut demonstrieren lassen. Wählen Sie Einfügen[Daten] > Signal > Wobbelkosinus. Richten Sie die Wobbelkosinus-Funktion  mit der Frequenz 1 und der 2. Frequenz 10000 ein. Bestimmen Sie auf der Registerkarte Abtastung die X-Komponente mit einem Startwert 0, einem Endwert 0,5 und einer Werteanzahl 10000.

IIR-Filter

Markieren Sie den Datensatz Signal.

Klicken Sie auf Sie Einfügen[Analysen] > Analyse-Assistent.

Wählen Sie die Kategorie IIR Filter unter Filter aus. Dort wählen Sie IIR-Filter aus. Klicken Sie auf die Weiter-Schaltfläche.

Der Schritt 2 des Analyseassistenten enthält einen interaktiven Dialog, in dem unterschiedliche Filtertypen und Filtercharakteristika ausgewählt werden können. Im Vorschaufenster des Analyseassistenten sind drei Diagramme abgebildet. Zu sehen ist das Eingangssignal, die Filterspezifikation und das gefilterte Signal bzw. ein Diagramm mit den Filterkoeffizienten. Mit der Option Amplitudengang anzeigen haben Sie die Möglichkeit, den Amplitudengang im Diagramm mit der Filterspezifikation ein- bzw. auszublenden. Der Amplitudengang wird zusätzlich in logarithmischer Darstellung angezeigt.

Wählen Sie als Filtertyp Hochpass und als Filtercharakteristik Tschebyscheff. Mit diesem Filter lässt sich die Welligkeit im Durchlassbereich beeinflussen. Schalten Sie die Option Normierte Frequenzen verwenden ein. Als Filterspezifikation wählen Sie die Ordnung 7, die normierte Grenzfrequenz Fg1 0,25 und als Fehler im Durchlassbereich den Wert 0,2. Betrachten Sie nun die erzeugte Filterspezifikation, so zeigt sich, dass sich die Welligkeit des Filters im Durchlassbereich im Bereich von 0,8 bis 1 bewegt, also einen maximalen Fehler von 0,2 aufweist. Wenn Sie die Welligkeit reduzieren, geht dies auf Kosten der Filtersteilheit im Übergangsbereich.

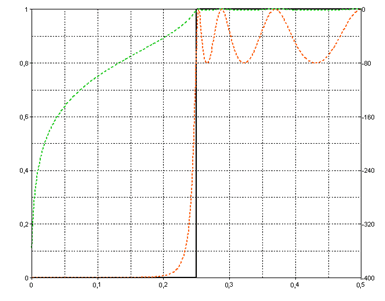
Im Gegensatz zum Tschebyscheff-Filter lässt sich für das Inverse Tschebyscheff-Filter die Welligkeit im Sperrbereich angeben. Der Filterentwurf für das Cauer-Filter ist noch flexibler, da sowohl die Welligkeit im Durchlassbereich als auch die Welligkeit im Sperrbereich definierbar ist.

Für die IIR-Filter lässt sich eine feste Filterordnung angeben. Daneben ist es auch möglich, die Filterordnung in Bezug auf die angegebene Spezifikation zu berechnen. Statt der normierten Grenzfrequenz werden für einen Übergangsbereich jeweils eine untere und obere Grenze angegeben. Außerdem wird sowohl der Fehler im Durchlassbereich als auch der Fehler im Sperrbereich angegeben. Das gefilterte Signal darf laut Spezifikation diese Fehler an den definierten Bandgrenzen nicht unter- bzw. überschreiten.

Wählen Sie als Ordnung Berechnen und als Übergang die normierten Frequenzen 0,24 und 0,26. Für die beiden Fehler geben Sie jeweils 0,1 ein. Sie können statt der Fehler auch die Welligkeit im Durchlassbereich bzw. die Dämpfung im Sperrbereich in Dezibel angeben. Wenn Sie den Modus ändern, so werden die Werte entsprechend umgerechnet.

Ausgabe-Optionen des Analyseassistenten

Um sich die Objekte, die der Analyseassistent automatisch erzeugt, anzusehen, klicken Sie auf Weiter. Machen Sie in Schritt 3 an die beiden aktiven Optionen einen Haken und klicken Sie anschließend auf Beenden.

Sieben Objekte wurden in der FlexPro-Projektdatenbank erzeugt.

IIRFilter ist das Analyseobjekt. Es führt die Filterung aus. Sie können das Objekt durch einen Doppelklick öffnen.

Spezifikation ist die Formel zur Erzeugen der Spezifikation, die bei der Darstellung benutzt wird.

Amplitudengang ist die Formel zur Erzeugen des Amplitudengang des Filters, die ebenfalls bei der Darstellung benutzt wird.

Das Diagramm Signal enthält das Eingangssignal, das Diagramm IIRFilter ist die Darstellung des gefilterten Signals bzw. der Koeffizienten des Filters und das Diagramm Spezifikation bildet die Filterspezifikation ab.

Das Dokument IIRFilter beinhaltet die drei erzeugten Diagramme.

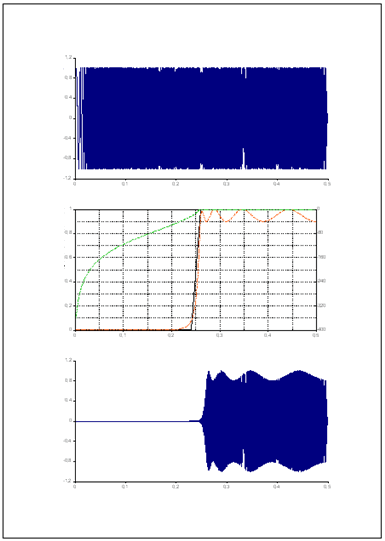
Die Ordnung der IIR-Filter ist auf 10 beschränkt, da es bei höheren Ordnungen zu Instabilitäten kommt. Lassen Sie uns daher nun den FIR-Filterentwurf betrachten, der höhere Ordnungen zulässt und zudem flexibler als der IIR-Filterentwurf ist.

FIR-Filter

Im Gegensatz zum IIR-Filterentwurf stehen für den FIR-Filterentwurf zwei unterschiedliche Rechenverfahren zur Verfügung, der Filterentwurf mittels Fensterung und der FIR-Equiripple Algorithmus (Parks-McClellan Verfahren).

FIR-Filterentwurf mittels Fensterung

Wir verwenden wiederum das synthetische Signal. Markieren Sie den Datensatz Signal.

Klicken Sie auf Sie Einfügen[Analysen] > Analyse-Assistent.

Wählen Sie die Kategorie FIR Filter unter Filter aus. Dort wählen Sie Fenster-Methode aus. Klicken Sie auf die Weiter-Schaltfläche. Wählen Sie Gefiltertes Signal als Ergebnis und Bandpass als Filtertyp. Schalten Sie die Option Normierte Frequenzen verwenden ein. Verwenden Sie das Hamming-Fenster mit den Grenzfrequenzen Fg1 gleich 0,1 und Fg2 gleich 0,4 und einer Filterlänge 71. Klicken Sie auf die Fertigstellen-Schaltfläche. Wenn Sie nun das Eingangssignal und das eben erstellte Filterobjekt markieren und ein Liniendiagramm erstellen, so werden Sie eine Phasenverschiebung zwischen den beiden Signalen erkennen. Diese Phasenverschiebung können Sie entfernen, indem Sie auf der zweiten Seite des Assistenten als Ergebnis Gefiltertes Signal mit Phasenkorrektur auswählen. Bei den FIR-Filtern handelt es sich um eine konstante Phasenverschiebung, die nur von der Filterlänge und der Abtastrate des Signals abhängig ist. Beim IIR-Filterentwurf ist ebenfalls eine Phasenkorrektur möglich. Allerdings findet dort eine Phasenkorrektur statt, indem das Signal zweimal gefiltert wird, einmal von vorne und einmal von hinten.

Markieren Sie nun nochmals das Signal und gehen Sie zurück in den Assistenten für den Filterentwurf mittels Fensterung. Die verschiedenen Fenstertypen weisen ein unterschiedliches Dämpfungsverhalten auf. Wenn die Option Amplitudengang anzeigen aktiviert ist, so wird im Diagramm mit der Spezifikation mit Ausnahme des Verallgemeinerten Hamming-Fenster die Sperrdämpfung als horizontale Linie eingezeichnet. Für die Fenster Rechteck, Bartlett, Hamming, Hanning und Blackman ist die Dämpfung fest (Fenstermethode). Für das Verallgemeinerte Hamming-Fenster lässt sich die Sperrdämpfung über den Parameter Alpha, der im Bereich zwischen 0 und 1 liegen kann, beeinflussen. Die beiden flexibelsten Fenster sind das Kaiser- und das Tschebyscheff-Fenster, da hier aus zwei der drei Parameter Filterlänge, Dämpfung und Übergang der dritte Parameter berechnet werden kann.

Wählen Sie auf der zweiten Seite des Assistenten als Ergebnis Filterkoeffizienten. Im unteren Diagramm wird nun statt dem gefilterten Signal die Impulsantwort (entspricht den Filterkoeffizienten) angezeigt. Wählen Sie zur Erzeugung eines Bandpasses das Kaiser-Fenster mit den Grenzfrequenzen Fg1 gleich 0,1 und Fg2 gleich 0,4. Unter Berechnung von wählen Sie Filterlänge. Spezifizieren Sie einen Filter mit einer Dämpfung von 20 dB und einem Übergang von 0,01. Mit dieser Methode erzielen wir eine Filterlänge von 94.

Nun wollen wir ein Filter mit der eben beschriebenen Filtercharakteristik mit Hilfe der FIR-Equiripple Methode entwerfen, um die beiden Verfahren für den FIR-Filterentwurf miteinander vergleichen zu können.

FIR-Filterentwurf mittels Equiripple Methode

Wählen Sie im Analyseassistenten die Kategorie FIR Filter unter Filtern aus. Dort wählen Sie Equiripple-Methode aus. Klicken Sie auf die Weiter-Schaltfläche.

Wählen Sie nun als Ergebnis Filterkoeffizienten, als Filtervorlage Bandpass und lassen Sie sich die Filterlänge berechnen. Schalten Sie die Option Normierte Frequenzen verwenden ein. Für einen Bandpass sind in der Liste mit den Bändern drei Bänder vordefiniert. Für jedes Band können die untere und obere Bandgrenze, die dazugehörigen Verstärkungsfaktoren und der Approximationsfehler bzw. die Gewichtung eingegeben werden. Der Übergang zwischen einem Sperrbereich und einem Durchlassbereich bildet sich aus der Differenz zwischen der oberen Bandgrenze eines Bandes und der unteren Bandgrenze des darauf folgenden Bandes. Durch Doppelklick auf die Listeneinträge können Sie die einzelnen Werte bearbeiten. Für die vordefinierten Filtervorlagen sind allerdings gewisse Einträge wie die Verstärkungsfaktoren gesperrt. Geben Sie nun folgende Werte in die Liste ein:

Für diesen Filter ist mit der FIR-Equiripple Methode eine Filterlänge von 77 notwendig. Sowohl der Durchlass- als auch der Sperrbereich besitzt eine gleichmäßige Welligkeit. Die Filter werden daher auch Equiripple-Filter genannt. Beim IIR-Filterentwurf ist eine gleichmäßige Welligkeit im Durchlass- und Sperrbereich mit Hilfe des Cauer-Filters möglich. Allerdings bewegt sich dort die Welligkeit nicht im Bereich von 1±δ, sondern zwischen 1-δ und 1.

Mit der FIR-Equiripple Methode lassen sich in Bezug auf die Spezifikation optimale Filter entwerfen. Das Ergebnis sind Filter mit niedrigerer Filterlänge als beim Filterentwurf mittels Fensterung. Die FIR-Equiripple Methode hat zudem den Vorteil, dass sich Multiband-Filter entwerfen lassen.

Entwurf eines Multiband-Filters

Für den Multiband-Filterentwurf wird ein Signal verwendet, das vier Sinuskurven mit gleicher Leistung, die sich über den Nyquist-Bereich erstrecken und drei Sinuskurven niedriger Leistung, die sich dazwischen befinden, enthält. Die Komponenten mit niedriger Leistung liegen -40 dB, -50 dB und -60 dB unter den Referenzsinuskurven. Außerdem wird weißes Rauschen so hinzugefügt, dass sich das Hintergrundrauschen bei ungefähr -75 dB befindet.

Die sieben Sinuskurven sehen folgendermaßen aus:

1.0*sin(2π*x*1005+π/2)+ (0dB)

1.0*sin(2π*x*2005+π/2)+ (0dB)

1.0*sin(2π*x*3005+π/2)+ (0dB)

1.0*sin(2π*x*4005+π/2)+ (0dB)

0.01*sin(2π*x*1505+π/2)+ (-40dB)

0.003162*sin(2π*x*2505+3π/2)+ (-50dB)

0.001*sin(2π*x*3505+π) (-60dB)

Der X-Wert (Zeit) variiert von 0 bis 0,1 bei einer Schrittweite von 0,0001. Die Nyquist-Frequenz ist somit 5000 (Hälfte der Abtastfrequenz von 10000). Die vier Referenzsinuskurven erstrecken sich über den Nyquist-Bereich. Die erste Sinuskurve mit geringer Leistung (-40dB) hat 1% der Amplitude der Referenzsinuskurven und 0,01 % Leistung von einer der Referenzsinuskurven. Die zweite Sinuskurve geringer Leistung (-50dB) hat 0,001 % der Leistung der Referenzkurven. Die letzte Testkurve (-60 dB) hat nur 0,1% der Amplitude und 0,0001 % der Leistung der Referenzkurven. Gauss-Rauschen (bei 0,15 %) wurde hinzugefügt, um ein Hintergrundrauschen bei ungefähr -75 dB zu erzeugen. Dieses Signal ist auch im Tutorial Spektralanalyse zu finden.

Wählen Sie Datei > Projektdatenbank öffnen und öffnen Sie die Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Tutorials\Filter.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021>Examples>Tutorials>Filter.fpd.  Markieren Sie den Datensatz Signal2. Klicken Sie auf Sie Einfügen[Analysen] > Analyse-Assistent. Wählen Sie die Kategorie FIR Filter unter Filtern aus. Dort wählen Sie die Equiripple-Methode aus. Klicken Sie auf die Weiter-Schaltfläche.

Wir werden nun einen Multiband-Filter entwerfen, der alle Signalanteile bis auf die Sinuskurven bei 1000 und 3000 Hz herausfiltert. Dazu wählen Sie als Ergebnis Gefiltertes Signal mit Phasenkorrektur und Multiband als Filtervorlage. Schalten Sie die Option Normierte Frequenzen verwenden ein. Lassen Sie sich die Filterlänge berechnen. Fügen Sie in der Liste insgesamt soviel Bänder hinzu, bis darin insgesamt 5 Bänder vorhanden sind. Geben Sie nun folgende Werte in die Liste ein:

Diese Einträge können Sie nun als Filtervorlage abspeichern, um sie zu einem späteren Zeitpunkt wieder verwenden zu können. Dazu tragen Sie unter Filtervorlage den Namen Multi1 ein und drücken anschließend die Speichern-Schaltfläche. Wenn Sie in der Liste anschließend noch einmal eine Änderung vornehmen, so müssen diese erneut abspeichern. Klicken Sie auf die Fertigstellen-Schaltfläche. Die Vorlagen speichert FlexPro in Ihrem Benutzerprofil.

Sie können nun mit einer einfachen FFT das Ergebnis überprüfen. Darüber hinaus haben Sie mit Option Spektralanalyse noch mehr Analysemöglichkeiten, wie z.B. die Erstellung einer Übertragungsfunktion aus dem Eingangssignal und dem gefilterten Signal.

Filterentwurf anhand eines vordefinierten Amplitudengangs

Zum Schluss des Tutorials werden wir mittels der FIR-Equiripple-Methode ein Filter entwerfen, bei dem die Verstärkungsfaktoren bzw. der Amplitudengang als Datensatz angegeben wird. Markieren Sie den Datensatz Signal. Öffnen Sie erneut den Analyseassistenten und wählen die FIR-Equiripple-Methode. Machen Sie anschließend folgende Einstellungen: Filtervorlage benutzerdefiniert, Filterlänge berechnen, Gewichtung aus Liste. Schalten Sie die Option Normierte Frequenzen verwenden ein. Definieren Sie folgende Bänder:

Wählen Sie nun als Verstärkungsfaktor den Datensatz Amplitude. Bei diesem Datensatz handelt es um den Amplitudengang, der aus einer IIR-Bandsperre (Cauer-Filter) erzeugt wurde. Wenn Sie sich nun die Spezifikation ansehen, so sehen Sie, dass die Filterspezifikation nicht mehr durch Konstanten im Sperr- und Durchlassbereich definiert ist, sondern durch den angegebenen Datensatz.

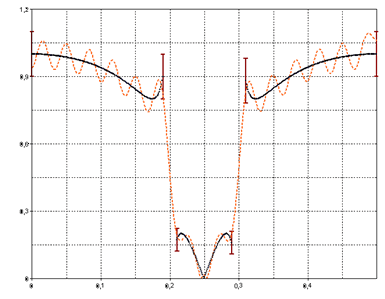
Es ist auch möglich, nur ein einziges Band über den gesamten normierten Frequenzbereich von 0 bis 0,5 zu definieren. Allerdings sollten Sie darauf achten, dass die einzelnen Bänder keine Sprungstellen aufweisen, da der Algorithmus sonst nicht konvergiert. Prinzipiell lässt sich sagen, dass der Filterentwurf anhand eines vordefinierten Amplitudengangs sehr rechenintensiv ist, wenn die Filterlänge berechnet werden soll. Außerdem konvergiert der Algorithmus je nach vorgegebener Spezifikation nicht sehr gut. In diesem Fall müssen die Approximationsfehler erhöht werden bzw. die Grenzfrequenzen der Bänder verändert werden.

Wenn die Filterlänge fest angegeben wird, so können die Gewichtungen der Bänder ebenfalls durch einen Datensatz angegeben werden.

Filterung mehrerer Eingangssignale

Sie haben auch die Möglichkeit, mehrere Signale gleichzeitig mit dem Analyseassistenten zu filtern. Dazu markieren Sie die zu filternden Signale, öffnen den Analyseassistenten und wählen als Ergebnis Gefiltertes Signal bzw. Gefiltertes Signal mit Phasenkorrektur. Der Analyseassistent erzeugt ein Analyseobjekt, das die Filterkoeffizienten berechnet. Zusätzlich wird für jedes Eingangssignal eine FPScript-Formel angelegt, die das Eingangssignal anhand der berechneten Filterkoeffizienten filtert.

Vergleich IIR- und FIR-Filter

In diesem Tutorial wurden verschiedene Entwurfsmethoden sowohl für IIR- als auch für FIR-Filter vorgestellt. Es stellt sich natürlich die Frage, ob IIR-Filter oder FIR-Filter vorzuziehen sind. Beide Filtertypen haben sowohl Vor- als auch Nachteile. Daher lässt sich diese Frage nicht eindeutig beantworten. Hier sind einige Punkte aufgelistet, die Sie bei Ihrer Entscheidung unterstützen sollen:

IIR-Filter

Vorteile:

•Einfache Berechnung, da sich viele frequenzselektive Filter mit geschlossenen Entwurfsformeln berechnen lassen

•Amplitudengang-Spezifikation mit IIR-Filtern am effizientesten

•Geringere Gruppenlaufzeit als FIR-Filter

•Geringere Filterlänge erforderlich

Nachteile:

•keine lineare Phase

•Variable Gruppenlaufzeit

•sind nur stabil, wenn alle Polstellen innerhalb des Einheitskreises liegen

FIR-Filter

Vorteile:

•Entwurf von Filtern mit linearer Phase möglich

•sind immer stabil (enthalten nur Nullstellen in der Übertragungsfunktion)

•Konstante Gruppenlaufzeit

Nachteile:

•aufwendige iterative Verfahren notwendig

•viele Koeffizienten sind für Realisierung steiler Filter erforderlich (höhere Filterordnung als bei IIR-Filtern notwendig

Die FIR-Equiripple Methode führt zu Filtern niedrigerer Ordnung als die Fenster-Methode und bietet mehr Gestaltungsmöglichkeiten (Gewichtung, Approximationsfehler) bei der Filterspezifikation. Außerdem lassen sich mit der FIR-Equiripple Methode Multiband-Filter entwerfen.

Literatur

Gute Einführungen in die digitale Filterung sind:

•Oppenheim, A. V. and Schafer, R. W. (1999). Discrete-Time Signal Processing, 2nd Edition. Prentice Hall, New Jersey.

•Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, New York.

Die in FlexPro verwendeten Filter-Algorithmen sind hier beschrieben:

•J.H. McClellan, T.W. Parks, L.R. Rabiner. A Computer Program for Designing Optimum FIR Linear Phase Digital Filters. IEEE Transactions on Audio and Electroacoustics, Vol. AU-21, No.6, December 1973

•L. R. Rabiner, J. H. McClellan and T. W. Parks. FIR Digital Filter Design Techniques Using Chebyshev Approximation. Proceedings IEEE, Vol. 63, No. 4, pp. 595 610, April 1975

•L. R. Rabiner, C. A. McGonegal and D. Paul (1979). FIR Windowed Filter Design Program - WINDOW. Section 5.2 in Programs for Digital Signal Processing, IEEE Press, pp. 5.2-1 to 5.2-19.

Siehe auch

Option Digitale Filter

Analyseassistent

Analyseobjekt FIR-Filter (Fenster-Methode)

Analyseobjekt FIR-Filter (Equiripple-Methode)

Analyseobjekt IIRFilter

Fenster-Methode

FIR-Equiripple-Methode