Mit diesem Analyseobjekt können Sie eine Kreisapproximation, d.h. eine kreisförmige Kurvenanpassung an die zugrundeliegenden Daten durchführen. Verwenden Sie die Kreisapproximation für die Auswertung von Rundheitsmessungen und die Bewertung von Wellenschwingungen (siehe [1], [2] [4]). Es stehen Ihnen die LSCI, MCCI, MICI, MZCI -Kreisapproximationsverfahren sowie ein elementares Kreisapproximationsverfahren (analog zu ISO-Norm 7919-1 aus [3]) zur Verfügung.

Zudem können Sie zirkuläre Ausreißer aus den Daten entfernen und ein Gauß-Filter zur Glättung vor Durchführung der Kreisapproximation anwenden. Die zugrundeliegenden Daten werden im Folgenden auch als Profil bezeichnet.

Beschreibung und Ausgaberesultate

Die LSCI, MCCI, MICI, MZCI -Kreisapproximationsverfahren berechnen einen oder mehrere Referenzkreise, die je nach gewähltem Verfahren unterschiedlich ermittelt werden:

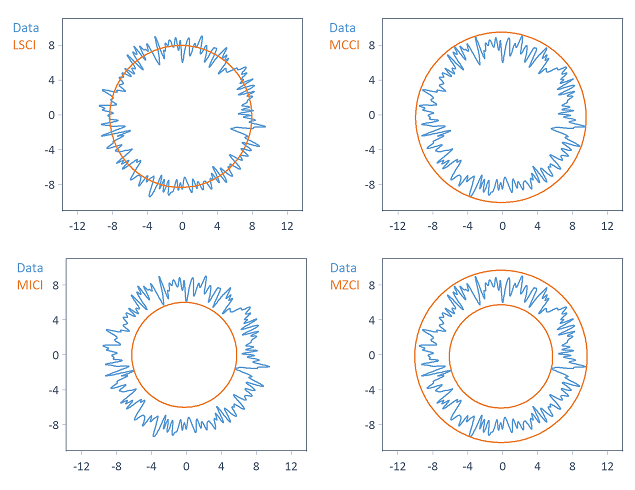
Hinweis   Je nach gewählten Kreisapproximationsverfahren können die Kreiszentrumskoordinaten der Referenzkreise mehr oder weniger stark voneinander abweichen.

Vom Referenzkreis (bzw. den Referenzkreisen) werden Innenkreis, Mittelkreis und Außenkreis abgeleitet und berechnet (jeweils mit gleichem Kreiszentrum wie der Referenzkreis). Als Ergebnisse kann das Analyseobjekt die Kreise, statistische Kennwerte (z.B. Kreisradien und Kreiszentrumskoordinaten) und die vorgefilterten Daten zurückgeben. Die Werteanzahl der Kreise können Sie als Parameter vorgeben.

Als statistischer Kennwert steht in allen Fällen die Rundheit zur Verfügung (auch Rundheitsabweichung genannt). Diese berechnet sich stets als Differenz von Außenkreisradius zu Innenkreisradius (und ergibt sich also als eine vom jeweiligen Referenzkreis abgeleitete Größe). Die Rundheitsabweichung ist ein Maß für die Rundheit des gemessenen Profils. Für das LSCI-Verfahren und das elementare Kreisapproximationsverfahren (Kreiszentrumsbestimmung durch Mittelwertberechnung der Kreisbahn) werden weitere statistische Kennwerte wie unten beschrieben berechnet und ausgegeben.

Folgendes Bild visualisiert die ausgegebenen Kreise und statistischen Kennwerte für das Beispiel des LSCI-Kreisapproximationsverfahrens:

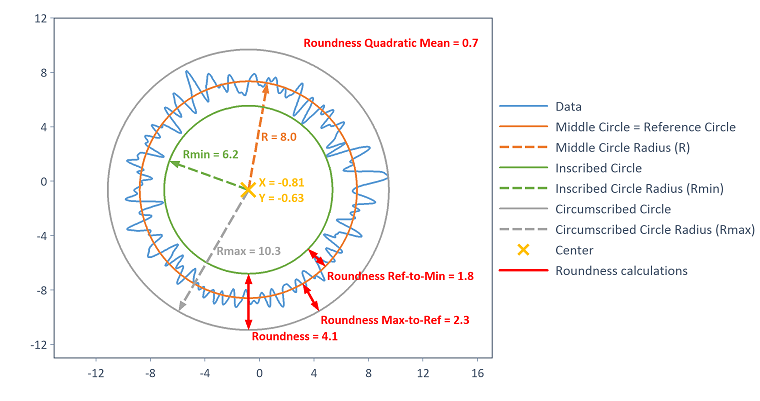
LSCI - Referenzkreis der kleinsten Abweichungsquadrate (Least Squares Circle)

Die Berechnung des LSCI-Referenzkreises basiert auf der LeastSquaresCircle-Funktion. Der LSCI-Kreis berechnet sich als der Kreis, bei dem die Summe der Quadrate der Abweichungen zu den Daten minimal wird. In der Literatur wird dieser ebenso als Gauß-Kreis bezeichnet. Der Innenkreis ergibt sich dann als der auf das Kreiszentrum des LSCI-Kreises bezogene größte innere Kreis. Der Außenkreis ergibt sich als der auf das Kreiszentrum des LSCI-Kreises bezogene kleinste äußere Kreis. Der Mittelkreis entspricht dem Referenzkreis, d.h. dem LSCI-Kreis.

Für die Berechnung des LSCI-Kreises stehen Ihnen die folgenden beiden Algorithmen zur Verfügung:

Als statistische Kennwerte werden beim LSCI-Verfahren zusätzlich zur Rundheitsabweichung ebenso die Spitze-zu-Referenz Rundheitsabweichung (Differenz von Außenkreisradius und Referenzkreisradius), die Referenz-zu-Tal Rundheitsabweichung (Differenz von Referenzkreisradius und Innenkreisradius) sowie der quadratische Mittelwert der Abweichungen der Datenpunkte zum Referenzkreis ausgegeben (gemäß [1]).

MCCI -  Kleinster umschriebener Referenzkreis (Minimum Circumscribed Circle)

Die Berechnung des MCCI-Referenzkreises basiert auf der MinimumCircumscribedCircle-Funktion. Der Referenzkreis berechnet sich bei diesem Verfahren als der Kreis mit dem kleinstmöglichen Durchmesser, der von außen an das Profil gelegt werden kann. Dieser wird auch als Hüllkreis bezeichnet. Der Außenkreis entspricht also bei diesem Verfahren dem Referenzkreis. Der Innenkreis ergibt sich als der auf das Kreiszentrum des Referenzkreises bezogene größte innere Kreis. Der Mittelkreis ist hier ebenso definiert als der arithmetisch gemittelte Kreis zwischen Referenzkreis (d.h. Außenkreis) und Innenkreis.

Für die Berechnung des MCCI-Kreises benötigt der dahinterliegende Algorithmus die Berechnung der konvexen Hülle. Die konvexe Hülle kann mit einem der beiden nachfolgend genannten Verfahren berechnet werden:

MICI - Größter einbeschriebener Referenzkreis (Maximum Inscribed Circle)

Die Berechnung des MICI-Referenzkreises basiert auf der MaximumInscribedCircle-Funktion. Der Referenzkreis berechnet sich bei diesem Verfahren als der Kreis mit dem größtmöglichen Durchmesser, der von innen in das Profil gelegt werden kann. Dieser wird auch als Pferchkreis bezeichnet. Der Innenkreis entspricht also bei diesem Verfahren dem Referenzkreis selbst. Der Außenkreis ergibt sich als der auf das Kreiszentrum des Referenzkreises bezogene kleinste äußere Kreis. Der Mittelkreis ist hier definiert als der arithmetisch gemittelte Kreis zwischen Außenkreis und Referenzkreis (d.h. Innenkreis).

MZCI - Referenzkreise der minimalen Zone

Beim MZCI-Verfahren werden zwei Referenzkreise bestimmt. Die Berechnung basiert auf der MinimumZoneCircle-Funktion. Es werden hierbei zwei konzentrische Kreise ermittelt, die das Rundheitsprofil einschließen und den kleinstmöglichen radialen Abstand voneinander haben. Die Referenzkreise bestehen also aus dem Außenkreis und Innenkreis. Der Mittelkreis ist hier definiert als der arithmetisch gemittelte Kreis zwischen den beiden Referenzkreisen, d.h. dem Außenkreis und dem Innenkreis.

Für die Berechnung des MZCI-Kreises werden die zusätzlichen Parameter Iterationen und Schrittweite verwendet. Zur Erklärung der Parameter ist das Verständnis des MZCI-Algorithmus hilfreich: Die konzentrischen Referenzkreise der minimalen Zone werden im ersten Iterationsschritt durch die durch den Least-Squares Circle (LSCI) berechneten Innen- und Außenkreise geschätzt. Anschließend wird das Ergebnis iterativ verbessert. Um den Mittelpunkt der aktuellen konzentrischen Innen- und Außenkreise wird dazu mit Hilfe einer zweidimensionalen Normalverteilung (Standardabweichung entspricht der Schrittweite) ein neuer Punkt ausgewählt. Es wird geprüft, ob die auf den neuen Punkt neu berechneten konzentrischen Innen- und Außenkreise eine geringere Radiendifferenz als zuvor aufweisen. Falls ja, wird der Punkt zum neuen Mittelpunkt. Das Verfahren wird nun iterativ gemäß dem Wert des Parameters Iterationen N-mal wiederholt und die Referenzkreise der minimalen Zone daher sukzessive verbessert.

Für die Parameter Iterationen und Schrittweite stehen Ihnen die folgenden Auswahlmöglichkeiten zur Verfügung:

Kreiszentrumsbestimmung durch Mittelwertberechnung der Kreisbahn

Bei diesem Kreisapproximationsverfahren handelt es sich um ein sehr einfaches Verfahren, bei welchem das Kreiszentrum durch Mittelwertberechnung der X- und Y-Komponenten bestimmt wird. Das Kreiszentrum ist also a priori festgelegt. Ein Referenzkreis wird bei diesem Verfahren daher nicht bestimmt. Der Außenkreis ergibt sich als der auf das berechnete Kreiszentrum bezogene kleinste äußere Kreis und der Innenkreis ergibt sich als der auf das berechnete Kreiszentrum bezogene größte innere Kreis. Der Radius des Mittelkreises entspricht dem Mittelwert der Entfernungen der Datenpunkte vom Kreiszentrum. Dies legt den Mittelkreis fest. Es sei angemerkt, dass der so berechnete Mittelkreis als (initialer) Schätzwert für den LSCI-Kreis interpretiert werden kann (und ähnliche Ergebnisse liefert). Die Anwendung dieses Verfahrens ist nur dann sinnvoll, wenn die zugrundeliegenden Daten periodisch abgetastet sind (geschlossenes Profil).

Wenn als Ergebnis Referenzkreis(e) gewählt wurde, so werden stattdessen alle Kreise ausgegeben (d.h. Innen-, Mittel- und Außenkreis), da für dieses Verfahren kein Referenzkreis explizit vorliegt.

Hinweis   Dieses elementare Kreisapproximationsverfahren folgt dem Vorgehen aus ISO-Norm 7919-1, wo ebenso das Kreiszentrum durch Mittelwertberechnung der X- und Y-Komponenten berechnet wird (siehe [3]). Es sei aber angemerkt, dass in ISO-7919-1 keinerlei Innen-, Mittel- und Außenkreise definiert sind und demzufolge die Rundheitsabweichung, wie oben spezifiziert, nicht berechnet wurde. Analog zu den oben aufgeführten Verfahren werden hier aus Symmetrie- und Vergleichsgründen aber trotzdem die Innen-, Mittel- und Außenkreise sowie die Rundheitsabweichung als Ergebnis zur Verfügung gestellt.

Zudem werden weitere statistische Kenngrößen ausgegeben, die in ISO-Norm 7919-1 als Maß zur Bewertung der Wellenbahn aufgeführt sind. Diese sind:

Vorfilterung durch Entfernung zirkulärer Ausreißer

Vor Durchführung der Kreisapproximation können zirkuläre Ausreißer aus den Daten entfernt werden. Hierbei werden alle Datenpunkte entfernt, deren Abstand vom angegebenen Kreiszentrum größer als der einstellbare minimale Radius und kleiner als der einstellbare maximale Radius sind:

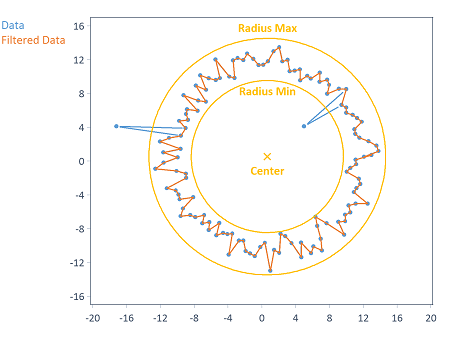
Die X- und Y-Koordinaten des Kreiszentrums können dabei entweder automatisch berechnet werden (als Mittelwert der jeweiligen X- und Y-Komponente der Eingangsdaten) oder explizit angegeben werden.

Vorfilterung mit einem Gauß-Filter

Vor Durchführung der Kreisapproximation kann das Rundheitsprofil mit einem Gauß-Filter vorgefiltert werden (siehe [2]). Es wird hierzu die GaussianFilter-Funktion verwendet. Mathematisch bedingt müssen zur Filterung die zugrundeliegenden Daten periodisch abgetastet sein (d.h. geschlossenes Profil).

Der Gauß-Filter wird hierbei gewöhnlich zur Glättung des Profils verwendet (Filtertyp-Einstellung: Tiefpass). Analog zu [2] kann der Gauß-Filter aber ebenso zur Hochpassfilterung des Profils verwendet werden. Ein Gauß-Bandpassfilter lässt sich durch Hintereinanderausführung eines Tiefpass- und Hochpassfilters realisieren.

Die für die Filterung einstellbare Grenzfrequenz geben Sie dabei in der Einheit UPR (Undulations Per Revolution) an. So entspricht 150 UPR beispielsweise der 150ten harmonischen Schwingung der Grundfrequenz. Die (normierte) Grundfrequenz muss also ebenfalls spezifiziert werden. Diese entspricht dem Kehrwert der Anzahl an Datenpunkten pro Umdrehung. Für die Angabe der Anzahl der Datenpunkte pro Umdrehung stehen Ihnen folgende Möglichkeiten zur Verfügung:

Die folgende Grafik zeigt ein mit einem Gauß-Filter geglättetes Profil (d.h. Tiefpassfilterung) mit Grenzfrequenz 50 UPR:

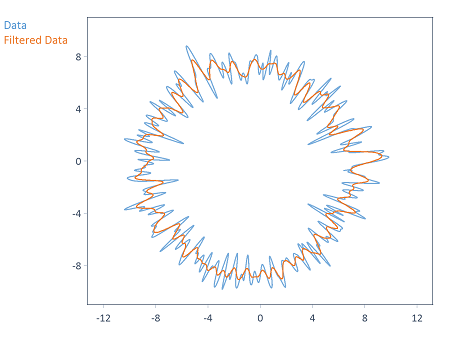
Daten als Polarkoordinaten

Die Eingangsdaten können sowohl in kartesischen Koordinaten als auch in Polarkoordinaten (Radius und Winkel) vorliegen. Dies können Sie auf der Registerkarte Daten des Analyseobjekts angeben. Die Y-Komponente entspricht dabei dem Radius und die X-Komponente dem Winkel.

Für die Winkeleinheit stehen Ihnen folgende Einstellungen zur Verfügung:

Falls eine Polarkoordinatendarstellung vorliegt, so werden die Daten vor Verrechnung in kartesische Koordinaten transformiert.

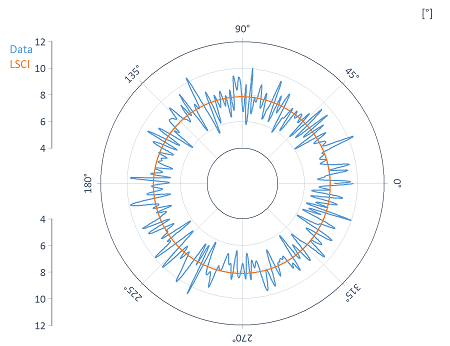
Die Resultate werden hingegen immer in kartesischen Koordinaten ausgegeben.In einem Polardiagramm können Sie diese aber polartransformiert darstellen, wie in folgendem Beispiel:

Literatur

[1] DIN Deutsches Institut für Normung e.V.Part 1: Vocabulary and parameters of roundness (DIN EN ISO 12181-1:2011), Geometrical product specifications (GPS)- Roundness, 2011.

[2] DIN Deutsches Institut für Normung e.V.Part 2: Specification operators (DIN EN ISO 12181-2:2011), Geometrical product specifications (GPS)- Roundness, 2011.

[3] DIN Deutsches Institut für Normung e.V. Measurements on rotating shafts and evaluation criteria, Part 1: General guidelines (DIN ISO 7919-1:1996), 1996.

[4] Verein Deutscher Ingenieure. Form measurement - Principles for the measurement of geometrical deviations (VDI/VDE 2631), 1999.]

Verwendete FPScript-Funktionen

LeastSquaresCircle

MaximumInscribedCircle

MinimumCircumscribedCircle

MinimumZoneCircle

GaussianFilter

Frequency

ValuesInInterval

Siehe auch

ConvexHull

* Dieses Analyseobjekt ist in FlexPro View und FlexPro Basic nicht verfügbar.