MaximumInscribedCircle (FPScript)
Berechnet den größten inneren Kreis (MICI) einer zweidimensionalen Punktemenge (Pferchkreis). Wird verwendet zur Rundheitsbestimmung.
Syntax
MaximumInscribedCircle(Points, [ OutputOptions = MICI_OUTPUT_INSCRIBED_CIRCLE ] [ , CircleSize = 5000 ])
oder
MaximumInscribedCircle(Y, X, [ OutputOptions = MICI_OUTPUT_INSCRIBED_CIRCLE ] [ , CircleSize = 5000 ])
Die Syntax der MaximumInscribedCircle-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Points |
Die Y- und X-Punktemenge, für die der größte innere Kreis (Pferchkreis) berechnet werden soll. Beide Komponenten des Signals müssen die gleiche Einheit besitzen. Erlaubte Datenstrukturen sind Signal. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. |
||||||||||||||||||||||
Y |
Die Y-Punktemenge, die zur Berechnung des größten inneren Kreises (Pferchkreis) verwendet wird. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Die Einheit muss mit der Einheit des Arguments X übereinstimmen. Erlaubte Datenstrukturen sind Datenreihe und Signal. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. |
||||||||||||||||||||||
X |
Die X-Punktemenge, die zur Berechnung des größten inneren Kreises (Pferchkreis) wird. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Die Einheit muss mit der Einheit des Arguments Y übereinstimmen. Erlaubte Datenstrukturen sind Datenreihe und Signal. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. |
||||||||||||||||||||||
OutputOptions |
Gibt an, welche Ergebnisse zurückgegeben werden sollen. Mehrere Ergebnisse werden als Liste ausgegeben. Wenn z. B. der Radius des Referenzkreises und die Rundheit ausgegeben werden sollen, so muss das Argument den Wert MICI_OUTPUT_INSCRIBED_CIRCLE_RADIUS + MICI_OUTPUT_ROUNDNESS enthalten. Das Argument OutputOptions kann folgende Werte haben:
Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert MICI_OUTPUT_INSCRIBED_CIRCLE gesetzt. |
||||||||||||||||||||||
CircleSize |
Gibt die Anzahl der Werte zur Darstellung der gefitteten Kreise an. Wenn Sie Null angeben, bleibt die ursprüngliche Werteanzahl erhalten. Das Argument wird nur berücksichtigt, wenn für OutputOptions einer der aufgelisteten Kreise gewählt wurde. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 0 sein. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 5000 gesetzt. |
Anmerkungen
Die Werte werden vor der Berechnung in 64-Bit Fließkommazahlen gewandelt.
Von der Punktemenge wird im ersten Schritt zuerst die Delaunay-Triangulation berechnet, um aus der Punktemenge ein Dreiecksnetz zu erzeugen (verwendeter Algorithmus mit Laufzeit O(n*log(n)): randomisierte inkrementelle Konstruktion aus [1]). Der größte Innenkreis entspricht dann dem Kreis mit dem größten Umfang aller in der Triangulation enthaltenen Dreiecke.
Die Ausgabeoptionen des Arguments OutputOptions sind im folgenden Diagramm visualisiert:
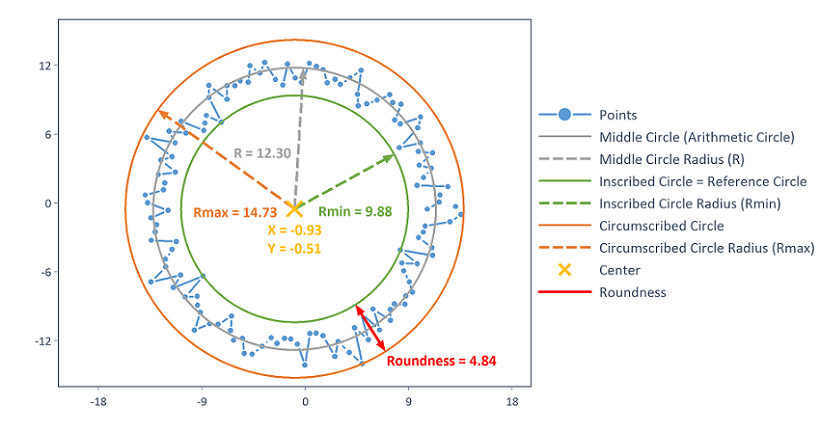
Auf die Ergebnisse kann mit folgenden Listenelementnamen zugegriffen werden:
Konstante |
Bedeutung |
|---|---|
.["Center_X"] |
X-Koordinate des Kreiszentrums des Referenzkreises. |
.["Center_Y"] |
Y-Koordinate des Kreiszentrums des Referenzkreises. |
.["Middle_Circle"] |
Arithmetisch gemittelter Mittelkreis zwischen Referenzkreis (größter innerer Kreis) und Außenkreis. |
.["Middle_Circle_Radius"] |
Radius des arithmetisch gemittelten Mittelkreises. |
.["Inscribed_Circle"] |
Referenzkreis (größter innerer Kreis). |
.["Inscribed_Circle_Radius"] |
Radius des Referenzkreises. |
.["Circumscribed_Circle"] |
Der auf den Referenzkreis bezogene kleinste Außenkreis. |
.["Circumscribed_Circle_Radius"] |
Radius des auf den Referenzkreis bezogenen kleinsten Außenkreises. |
.["Roundness"] |
Rundheitsabweichung als Differenz der Radien des Außen- und Innenkreises. |
Sie können auch stets die Syntax Formel.Listenelementname verwenden.
Hinweis Die MICI-Rundheitsberechnungen orientieren sich an der aktuell gültigen Norm zur Rundheitsbestimmung, siehe [2].
Verfügbarkeit
FlexPro Professional, Developer Suite
Beispiele
MaximumInscribedCircle(y, x)
Berechnet den größten inneren Kreis (MICI) einer Punktemenge.
MaximumInscribedCircle(y, x, MICI_OUTPUT_ROUNDNESS)
Berechnet den größten inneren Kreis (MICI) einer Punktemenge und gibt nur die Rundheit zurück.
MaximumInscribedCircle(points, MICI_OUTPUT_INSCRIBED_CIRCLE_RADIUS + MICI_OUTPUT_ROUNDNESS)
Berechnet den größten inneren Kreis (MICI) einer Punktemenge. Als Ergebnis wird der Radius des ermittelten Kreises und die Rundheit als Liste ausgegeben.
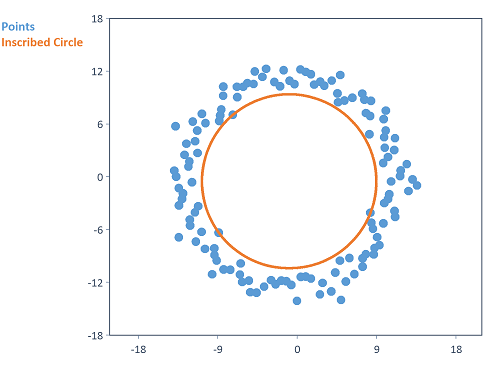
Dim alpha = Series(0, 2*PI, 0.05)
Dim r = 13.5 + Noise(1 # NumberOfRows(alpha), NOISE_NORMAL)
Dim points = Signal(Noise(1) + r*Sin(alpha), Noise(1) + r*Cos(alpha))
List("Points", points, "Inscribed Circle", MaximumInscribedCircle(points))
Berechnet den größten inneren Kreis (MICI) von zufällig verteilten Punkten in der zweidimensionalen Ebene.
Siehe auch
MinimumCircumscribedCircle-Funktion
Analyseobjekt Kreisapproximation
Literatur
[1] Leonidas J. Guibas, Donald E. Knuth, and Micha Sharir: Randomized Incremental Construction of Delaunay and Voronoi Diagrams. In: Algorithmica, Vol. 7, Pages 381-413. https://link.springer.com/article/10.1007/BF01758770,1992.
[2] DIN Deutsches Institut für Normung e.V.: Part 1: Vocabulary and parameters of roundness (ISO 12181-1:2011); English translation of DIN EN ISO 12181-1:2011. In: Geometrical product specifications (GPS)- Roundness. 2011.
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen