GaussianFilter (FPScript)
Filtert ein Signal mit einem Gauß-Filter. Wird gewöhnlich zur Glättung verwendet, sowie als Filter bei Rundheitsmessungen und Rundheitsanalysen.
Syntax
GaussianFilter(DataSet, Type, Fc1, [ Fc2 ], [ SamplingRate ] [ , Mode = GAUSSIANFILTERMODE_SYMMETRIC_EXTENSION ])
Die Syntax der GaussianFilter-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
DataSet |
Der zu filternde Datensatz. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal und Signalreihe. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Ungültige Werte sind in diesem Argument nicht zulässig. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||||
Type |
Gibt den Filtertyp an. Das Argument Type kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||
Fc1 |
Gibt die erste Eckfrequenz (Grenzfrequenz) des Gauß-Filters an. Die Frequenz muss zwischen 0 und 0,5 (die Hälfte der auf Eins normierten Abtastrate) oder zwischen 0 und 0,5 * SamplingRate liegen. Die Grenzfrequenz ist für den Gauß-Filter definiert als die Frequenz, bei der die Amplitude des Filters 50 Prozent der ursprünglichen Signalamplitude durchläuft. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Der Wert muss größer gleich 0 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||
Fc2 |
Gibt die zweite Eckfrequenz (Grenzfrequenz) des Gauß-Filters an. Die Frequenz muss zwischen 0 und 0,5 (die Hälfte der auf Eins normierten Abtastrate) oder zwischen 0 und 0,5 * SamplingRate liegen. Dieses Argument muss für einen Tiefpass oder Hochpassfilter nicht angegeben werden. Die Grenzfrequenz ist für den Gauß-Filter definiert als die Frequenz, bei der die Amplitude des Filters 50 Prozent der ursprünglichen Signalamplitude durchläuft. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Der Wert muss größer gleich 0 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||
SamplingRate |
Gibt die Abtastrate an. Das Argument ist optional. Wird das Argument nicht spezifiziert, so muss für die Eckfrequenzen Fc1 und Fc2 jeweils eine normierte Frequenz von 0 bis 0,5 angegeben werden. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Der Wert muss größer 0 sein. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||||
Mode |
Die Filterung entspricht der (schnellen) Faltung mit einer Gauß-Funktion im Zeitbereich. Das Argument spezifiziert also den Berechnungsmodus zur Durchführung der Faltung. Das Argument Mode kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert GAUSSIANFILTERMODE_SYMMETRIC_EXTENSION gesetzt. |
Anmerkungen
Der Gauß-Filter (Tiefpass) entspricht der Faltung mit folgender Gauß-Funktion (Faltungskern) im Zeitbereich:
In dieser Gleichung bezeichnet fc die Grenzfrequenz. Die Faltung wird hierbei mit Hilfe der FFT (schnellen Fouriertransformation) wie folgt berechnet: IRFFTn(FFTn(Data)*FFTn(GaussianKernel)). Da die Fourier-transformierte einer Gauß-Funktion wieder eine Gauß-Funktion ergibt, kann die Übertragungsfunktion (d.h. FFTn(GaussianKernel)) explizit berechnet werden. Im Frequenzbereich berechnet sich das Filter somit als Multiplikation mit der folgenden Übertragungsfunktion:
Für die Wahl von f = fc folgt, dass S(f) = 0.5, d.h. die Amplitude des Filters durchläuft 50 Prozent der ursprünglichen Signalamplitude.
Der Gauß-Hochpassfilter entspricht im Frequenzbereich der Multiplikation mit der Übertragungsfunktion 1-S(f). Der Bandpass- und Bandstopfilter ergibt sich entsprechend als Kombination von Tiefpass und Hochpass.
Für die folgende spezielle Wahl von fc, schreibt sich der Gauß-Kern im Zeitbereich äquivalent als Faltung mit einer Gauß-Normalverteilung (mit Erwartungswert 0 und Standardabweichung σ) als:
Die Struktur des Ergebnisses entspricht der des Arguments DataSet. Bei Datenmatrizen und Signalreihen erfolgt die Berechnung spaltenweise. Die X- bzw. Z-Komponenten werden, falls vorhanden, unverändert in das Ergebnis übernommen.
Hinweis Der Gauß-Filter kann insbesondere zur Glättung eingesetzt werden. Er wird außerdem häufig verwendet als Filter bei bei Rundheitsmessungen bzw. Rundheitsanalysen, siehe [1]. Der Modus GAUSSIANFILTERMODE_PERIODIC_BOUNDARY sollte hierbei verwendet werden, wenn es sich um einen periodischen Eingangsdatensatz bzw. ein geschlossenes Rundheitsprofil handelt. Für nicht-periodische Daten und transiente Daten ist der Modus GAUSSIANFILTERMODE_ZERO_BOUNDARY zu verwenden (entspricht Nullrandbedingung). Hierzu werden dem Eingangssignal eine geeignete Anzahl an Nullen für die Fouriertransformation angefügt (zero padding). Für nicht-periodische Daten mit unbekannter Randbedingung ist der Modus GAUSSIANFILTERMODE_SYMMETRIC_EXTENSION zu verwenden (genaue Randbedingung unbekannt, Daten werden symmetrisch verlängert). In aller Regel liefert dieser eine natürliche Glättung der Ränder.
Verfügbarkeit
Option Digitale Filter
Beispiele
GaussianFilter(Data, FILTER_LOWPASS, 0.04)
Glättet einen Datensatz mit einem Gauß-Tiefpassfilter mit Grenzfrequenz 0.04. Liefert in der Regel eine höhere Glättung als durch Glättung mit einem gleitenden Mittelwert mit der Smooth-Funktion.
GaussianFilter(Data, FILTER_HIGHPASS, 0.01)
Entfernt den DC-Anteil mit einem Gauß-Hochpassfilter mit kleiner Grenzfrequenz. Liefert ein ähnliches Ergebnis wie die DCRemovalFilter-Funktion.
Dim dirac = (0 # 100) : 1 : (0 # 100)
Dim gaussCoeff = GaussianFilter(dirac, FILTER_LOWPASS, 0.04)
AmplitudeResponse(gaussCoeff)
Berechnet den Amplitudengang des Gauß-Filters (Tiefpass mit Grenzfrequenz 0.04). Hierzu wird die GaussianFilter-Funktion auf einen Dirac-Stoß angewendet. Dies liefert die Übertragungsfunktion des Systems in Form der Filter-Koeffizienten. Mit Hilfe der Filter-Koeffizienten kann mit der AmplitudeResponse-Funktion der Amplitudengang des Filters berechnet werden. Die folgende Abbildung zeigt den Vergleich des Amplitudengangs des Gauß-Tiefpassfilters mit Grenzfrequenz 0.04 zu einem gleitenden Mittelwert mit Glättungsbreite 7 (siehe Smooth-Funktion). Hohe Frequenzen werden insbesondere wesentlich besser unterdrückt als durch den gleitenden Mittelwert:
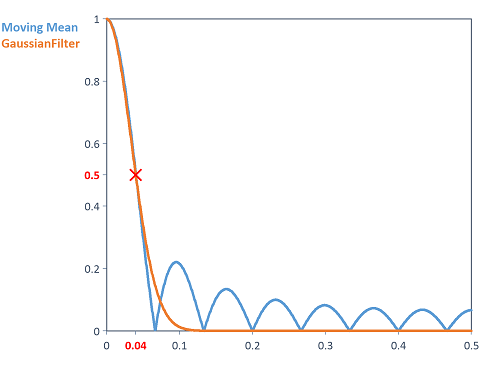
Die folgende Abbildung zeigt den Vergleich des Amplitudengangs des Gauß-Hochpassfilters mit Grenzfrequenz 0.04 zur DCRemovalFilter-Funktion mit gleicher Grenzfrequenz und Ordnung 2:
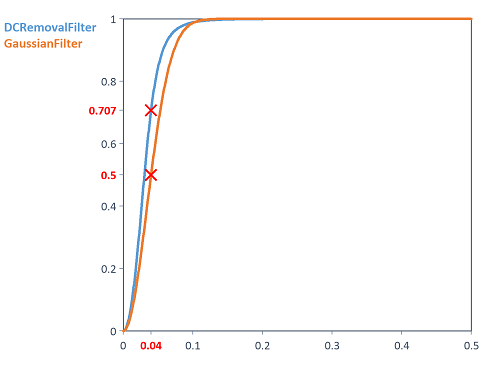
Dim sigma = 4.5
Dim fc = sqrt(log(2))/(sigma*sqrt(2)*PI)
GaussianFilter(Data, FILTER_LOWPASS, fc)
Glättet einen Datensatz durch Faltung mit einer Gauß-Normalverteilung mit einstellbarer Standardabweichung σ (Breite).
Siehe auch
MaximumInscribedCircle-Funktion
MinimumCircumscribedCircle-Funktion
Analyseobjekt Kreisapproximation
Literatur
[1] B. Muralikrishnan, J. Raja: Computational Surface and Roundness Metrology. Springer-Verlag London Limited,2009.ISBN 1-848-00296-3.
[2] DIN Deutsches Institut für Normung e.V.: Part 2: Specification operators (ISO 12181-2:2011); English translation of DIN EN ISO 12181-2:2011-07. In: Geometrical product specifications (GPS) - Roundness. 2011.
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen