Analyseobjekt Umdrehungssynchrone Abtastung (Option Ordnungsanalyse)
Das Analyseobjekt Umdrehungssynchrone Abtastung transformiert ein über der Zeit abgetastetes Signal in den Umdrehungsbereich. Das Signal liegt dann nicht mehr in zeitlich äquidistanten Schritten, sondern in äquidistanten Drehwinkelschritten (d.h. äquidistanten Umdrehungsintervallen) vor. In der Literatur wird das Verfahren auch als Synchronous Angular Sampling, Computed Order Tracking, Synchronous Sampling oder auch Adaptive Resampling bezeichnet.
Dies erlaubt auf effektive Weise die Durchführung einer Ordnungsanalyse, da das Frequenzspektrum (d.h. die Fourier-Transformation) des in den Umdrehungsbereich konvertierten Signals dann unmittelbar das sogenannte Ordnungsspektrum liefert:
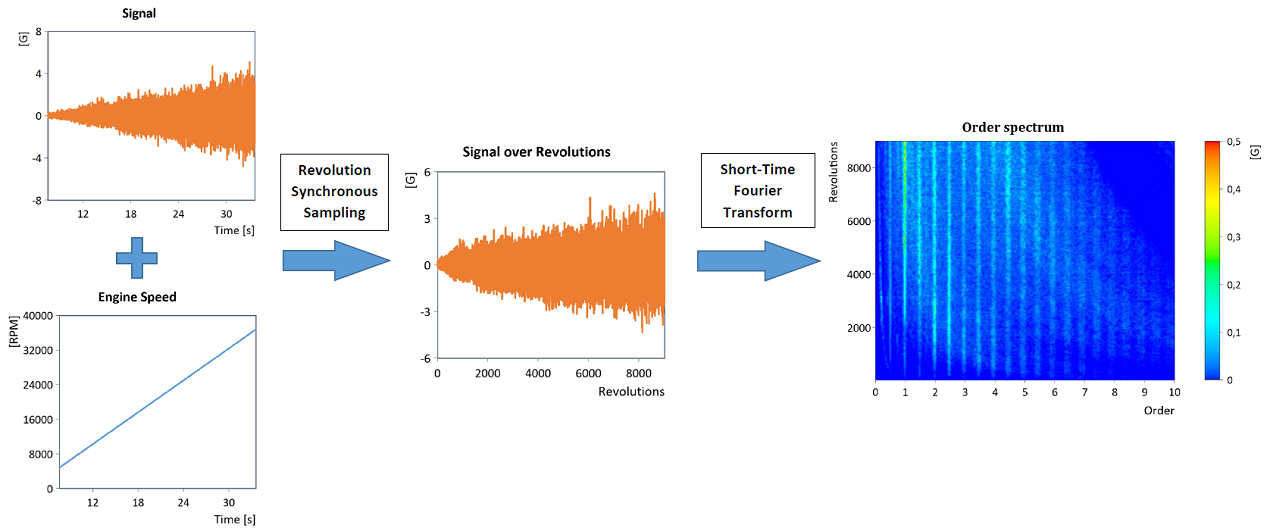
Genauso lässt sich durch gewöhnliche Bandpassfilterung (z.B. mit Hilfe eines geeigneten IIR-Bandpassfilter) im Umdrehungsbereich der Verlauf einzelner Ordnungen ermitteln (hier abgebildet der blockweise RMS-Verlauf der gefilterten Ordnungen):
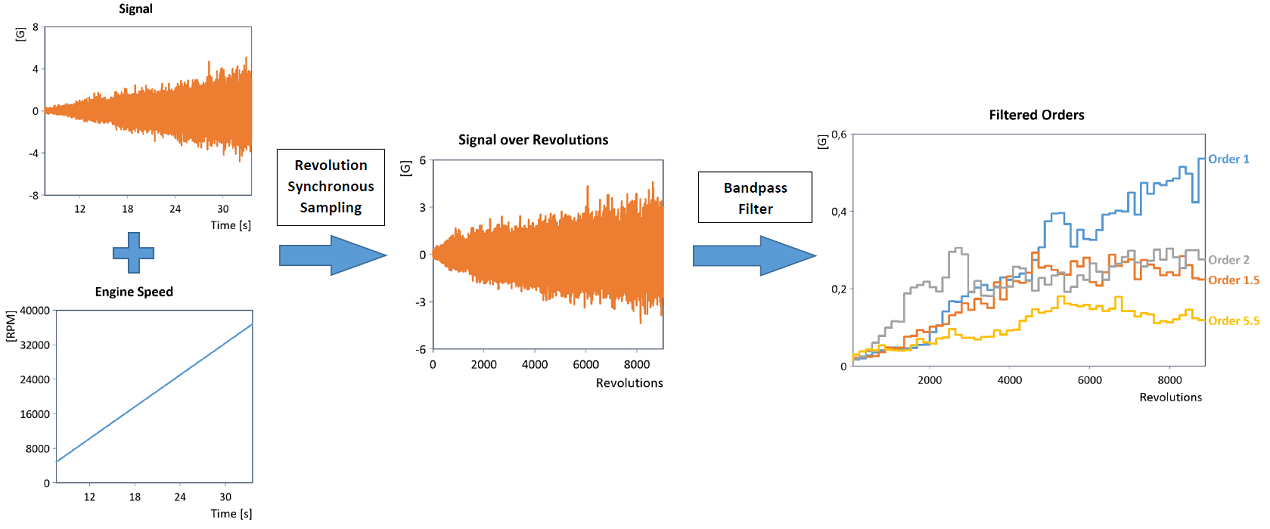
Bemerkung: die Fourier-Analyse im Umdrehungsbereich (z.B. Berechnung eines Ordnungsspektrums) sowie die Bandpassfilterung im Umdrehungsbereich können direkt in einem Schritt mit den Analyseobjekten Umdrehungssynchrone Ordnungsanalyse und Ordnungsfilter durchgeführt werden.
Registerkarte Daten
Diese Registerkarte spezifiziert die Eingangsdaten im Zeitbereich (Details siehe auch RevolutionSyncSampling):
Signale im Zeitbereich
Das für das Analyseobjekt zu transformierende Zeitsignal muss in der Datenstruktur Signal vorliegen. Die Drehzahl kann entweder in der Datenstruktur Signal (entspricht Hochlauf bzw. variabler Drehzahl) oder als Einzelwert (entspricht konstante Drehzahl oder Grundfrequenz) angegeben werden.
Bei fehlenden Einheiten oder ausgeschalteter Einheitenverwaltung, wird die Drehzahl stets in der Einheit [1/min] und die X-Komponente des Zeitsignals in der Einheit interpretiert.
Die Momentandrehzahl wird oft mit einem Impulsgeber gemessen, der eine bestimmte Anzahl von Impulsen pro Umdrehung erfasst. Sie können das hieraus resultierende Impulssignal direkt in ein Drehzahlsignal konvertieren. Markieren Sie hierzu die Option Drehzahl ist Impulssignal und geben Sie die Anzahl der Impulse pro Umdrehung an. Die Konvertierung des Impulssignals in ein Drehzahlsignal erfolgt mit der ImpulseToFrequency-Funktion.
Registerkarte Optionen
In dieser Registerkarte werden die Parameter zur Transformation vom Zeit- in den Umdrehungsbereich spezifiziert. Schematisch lässt sich der Algorithmus des Transformationsverfahrens wie folgt beschrieben (Details siehe auch RevolutionSyncSampling):

Umabtastung in den Umdrehungsbereich
Zur Umabtastung vom Zeit- in den Umdrehungsbereich stehen drei verschiedene Modi zur Verfügung. In den meisten praktischen Anwendungsfällen ist die lineare Umabtastung ausreichend:
Resample-Verfahren |
Beschreibung |
|---|---|
Lineare Interpolation |
Das Zeitsignal wird vor Überführung in den Umdrehungsbereich an den (nicht-äquidistanten) Zeitpunkten der äquidistanten Umdrehungsstützstellen mittels linearer Interpolation ausgewertet. Die Transformation ist dadurch schnell, kann aber Alias-Effekte bei anschließender FFT-Analyse des umdrehungssynchron abgetasteten Signals verursachen. |
Spline-Interpolation |
Das Zeitsignal wird vor Überführung in den Umdrehungsbereich an den (nicht-äquidistanten) Zeitpunkten der äquidistanten Umdrehungsstützstellen mittels Spline-Interpolation ausgewertet. Gegenüber dem linearen Resampling ist die Spline-Interpolation geringfügig langsamer, Alias-Effekte werden aber reduziert. |
FFT-Resampling |
Das Zeitsignal wird vor Überführung in den Umdrehungsbereich an den (nicht-äquidistanten) Zeitpunkten der äquidistanten Umdrehungsstützstellen durch FFT-Resampling ausgewertet. Hierbei wird das Zeitsignal zunächst in den Frequenzbereich transformiert, dort werden Nullen angehängt und anschließend wird wieder in den Zeitbereich zurücktransformiert. Die Umabtastung mittels Fourier-Transformation führt zu einem nahezu idealen Ergebnis, da dadurch keine hochfrequenten Signalanteile hinzugefügt werden. Alias-Effekte bei Berechnung des Ordnungsspektrums bleiben hierdurch nahezu aus, die Berechnungszeit nimmt aber deutlich zu. |
Bei Wahl des Splines- oder des FFT-Resampling-Verfahrens, muss ein Resample-Faktor spezifiziert werden, um den die Abtastrate des Signals beim Transformationsalgorithmus erhöht wird.
Unabhängig vom gewählten Resample-Verfahren, sind die Anzahl der Datenpunkte pro Umdrehung für das in den Umdrehungsbereich zu transformierenden Signals anzugeben. Dies bestimmt die Abtastung des transformierten Signals im Umdrehungsbereich. Gemäß Nyquist-Abtasttheorem bestimmt die Hälfte dieses Wertes die maximale Ordnung, die mittels Fourier-Analyse überhaupt berechnet werden kann.
Zur Bestimmung der Anzahl der Datenpunkte pro Umdrehung stehen zwei Modi zur Verfügung:
Datenpunkte pro Umdrehung |
Beschreibung |
|---|---|
Automatisch (Anpassung an max. Ordnung) |
Berechnet für die Anzahl der Datenpunkte pro Umdrehung einen automatischen Wert, so dass die theoretisch größte im Signal vorkommende Ordnung mittels Fourier-Analyse noch berechnet werden kann. Der automatisch berechnete Wert kann hierbei durch einen frei einstellbaren Begrenzungswert limitiert werden. |
Fester Wert |
Für die Anzahl der Datenpunkte pro Umdrehung kann ein beliebiger, fester Wert eingegeben werden. |
Trendkorrektur im Umdrehungsbereich
In vielen Anwendungsbeispielen führt ein vorhandener, zu großer DC-Offset zu einer visuell ungeeigneten Darstellung im Konturplot des Ordnungsspektrums, in welcher der DC-Anteil dominiert. Es ist daher vorteilhaft, den DC-Anteil herauszufiltern. Hierzu lässt sich für das in den Umdrehungsbereich transformierte Signal ein entsprechender DC-Offset-Hochpassfilter mit einstellbarer Grenzfrequenz (Abschneide-Ordnung) und Filterordnung (Filtersteilheit) einstellen (Details zum DC-Offset-Hochpassfilter siehe DCRemovalFilter-Funktion).
Ausgabe im Umdrehungsbereich
Es kann das in den Umdrehungsbereich transformierte Signal, der in den Umdrehungsbereich transformierte Drehzahldatensatz oder die in den Umdrehungsbereich transformierte Zeitkomponente zurückgegeben werden. Zulässig sind ebenso beliebige Kombinationen aus diesen Ausgabemöglichkeiten, welche dann in der Datenstruktur Liste zusammengefasst werden.
Beispiele
In der Projektdatenbank C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Order Tracking Analysis.fpd bzw. C:>Benutzer>Öffentlich>Öffentliche Dokumente>Weisang>FlexPro>2021\Examples\Order Tracking Analysis.fpd finden Sie Beispiele für die verschiedenen Anwendungsfälle und Modi, für die eine Ordnungsanalyse durchgeführt werden kann. Obige Diagramme sind dort insbesondere enthalten.
