Prony-Algorithmus
Der Prony-Algorithmus wird zur Bestimmung gedämpfter Sinuskomponenten in einem Signal verwendet.
Bei reellen Daten entspricht die Approximation komplexer Exponentialfunktionen der Approximation gedämpfter Sinusfunktionen. Eine Approximation ungedämpfter Spektralkomponenten wird dadurch erzielt, dass die Dämpfungsfaktoren auf dem Wert 0 festgehalten werden. Der implementierte Algorithmus wurde mehrfach modifiziert, um sein Verhalten bei verrauschten Signalen zu verbessern.
Die Prony-Algorithmen sind mehrstufige Verfahren:
1.Approximation eines AR (AutoRegressive) Modells
2.Ermittlung der komplexen Wurzeln des AR-Modells
3.Filterung der Wurzeln
4.Approximation der komplexen Amplituden nach der Methode der kleinsten Quadrate
5.Erzeugung des endgültigen Modells mit Signal/Rausch-Trennung (signal thresholding)
Komplex-exponentielles Modell
Ein Prony-Modell der Ordnung m besteht aus der Summe von komplexen Exponentialfunktionen z, die mit einer komplexen Amplitude h multipliziert sind.
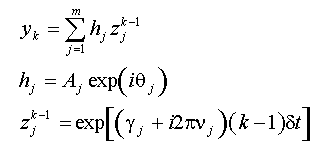
In den Gleichungen für h and z, ist A die Amplitude der Exponentialfunktion, g ist der Dämpfungsfaktor, u ist die Frequenz, und q ist die Phase. FlexPro gibt die komplexen Amplituden und Exponentialfunktionen als reelle, gedämpfte sinusförmige Funktionen aus:
A ist die ausgegebene Amplitude, k ist der Dämpfungsfaktor, u ist die Frequenz und q ist die Phase. Beachten Sie, dass das Modell mit k=0 auf ein ungedämpft sinusförmiges Modell und für u=0 und q=p/2 zu einem Exponentialmodell erster Ordnung reduziert wird.
Wurzeln des AR-Polynoms
Ein komplex-exponentielles Modell besteht aus den Parametern der komplexen Amplituden und Exponentialfunktionen. Die Frequenzen und Dämpfungskoeffizienten (Die Parameter der Exponentialfunktionen) werden zuerst geschätzt. Diese Werte werden von den komplexen Wurzeln des approximierten AR-Modells abgeleitet. Wenn das vorwärts gerichtete AR-Modell (forward prediction) für den gedämpften Fall verwendet wird, dann entsprechen die komplexen Wurzeln des AR-Polynoms den Exponentialparametern des Prony-Modells. Diese komplexen Wurzeln tragen nicht nur die Frequenzen sondern auch die exponentiellen Dämpfungsfaktoren. Ein entsprechender AR-Algorithmus wird eingesetzt.
Algorithmen zur Singulärwertzerlegung (SVD)
Die SVD-Algorithmen trennen Signal und Rauschen und erzeugen somit in der Regel genauere Frequenzen und Dämpfungswerte, da der Einfluss des Rauschens ausgeklammert wird.
Wie bei AR-Approximationen muss die Anzahl der Eigenmoden des Signal-Unterraumes dem Doppelten der Anzahl der zu erwartenden Komponenten entsprechen.
Auswahl der Wurzeln
Um den Prony-Algorithmus zu stabilisieren, führt FlexPro eine Filterung der Wurzeln in einem Zwischenschritt durch. Dieser Vorgang erfolgt automatisch. Negative Wurzeln sowie Wurzeln, die nahe an der Nyquist-Grenze liegen, werden eliminiert. Der Prony-Algorithmus kann Sinusschwingungen, gedämpfte Sinusschwingungen und reelle Exponentialfunktionen erkennen. Wenn eine AR-Wurzel bei der Frequenz 0 liegt, dann ist die Funktion eine reelle Exponentialfunktion. Liegt sie auf dem Einheitskreis, dann bezeichnet sie eine ungedämpfte Sinusschwingung. In anderen Fällen handelt es sich um gedämpfte Sinusschwingungen. Dies ergibt sich direkt aus den Wurzeln des AR-Polynoms und kann nicht beeinflusst werden.
Bitte beachten Sie, dass reelle Exponentialfunktionen herausgefiltert werden und daher im endgültigen Prony-Modell nicht mehr erscheinen.
Approximation der komplexen Amplituden
Nachdem die Wurzeln identifiziert wurden, werden die initialen Schätzungen für die komplexen Amplituden im Modell durch lineare Regression ermittelt. Aus diesen werden dann die Amplituden und Phasen abgeleitet.
Trennung von Signal und Rauschen
Da es sich bei der Prony-Methode um ein deterministisches Modell zur Approximation der komplexen Exponentialfunktionen handelt, kann das Signal jederzeit dadurch reduziert werden, dass man weniger signifikante Komponenten heraus nimmt und anschließend das Modell mit geringerer Anzahl von Komponenten neu berechnet. Das endgültige Prony-Modell enthält daher nur die Komponenten mit der höchsten Signifikanz, deren Anzahl durch ein vorgegebenes Maximum beschränkt ist.
Nachdem die Signalkomponenten paarweise zugeordnet wurden, wird die Approximation für die komplexen Amplituden erneut mit den Komponenten höchster Signifikanz durchgeführt. Die Approximation mit der reduzierten Komponentenanzahl ist stabiler und die Wahrscheinlichkeit, dass die darin enthaltenen Komponenten durch Rauschen verursacht wurden, ist geringer.
Literatur
Eine exzellente Beschreibung des Prony-Algorithmus finden Sie in:
•S. Lawrence Marple, Jr., "Digital Spectral Analysis with Applications", Prentice-Hall, 1987, p.303-349.