L'objet d'analyse Filtre d'ordres calcule l'analyse d'ordre pour les vibrations dépendant de la vitesse en filtrant par bande passante les ordres individuels. Les vibrations mesurées sur les machines tournantes présentent un spectre dans lequel les maxima se produisent à des fréquences correspondant à un multiple de la vitesse de la machine. L'apparition de ces maxima a deux causes différentes. D'une part, la machine peut être considérée comme un système de transmission non linéaire, qui est excité par une vibration harmonique correspondant à la vitesse de rotation. La non-linéarité génère des harmoniques de cette vibration de base, qui conduisent aux maxima correspondants. Par contre, une telle machine peut contenir des composants dont la vitesse n'est pas égale à la vitesse de base, mais correspond toujours à un multiple fixe de cette vitesse. Par exemple, les différents arbres d'une boîte de vitesses ont des vitesses différentes. Mais les dents d'un engrenage ou les billes d'un roulement à billes génèrent également des vibrations qui sont en relation fixe avec la vitesse. Si ce rapport entre la fréquence fondamentale d'un composant et la fréquence fondamentale de la machine est connu sous le nom d'ordre, alors les maxima individuels du spectre peuvent être spécifiquement attribués à un seul ou à quelques composants de la machine. Cela peut être utilisé, par exemple, pour isoler la cause des résonances.

Dans le procédé utilisé ici, une conversion de la fréquence d'échantillonnage du signal temporel est d'abord effectuée(rééchantillonnage synchrone en révolution) de sorte que le signal ne se présente plus en étapes temporellement équidistantes, mais en étapes d'angle de rotation équidistantes (c'est-à-dire en intervalles de rotation équidistants). Il s'agit d'une méthode efficace pour effectuer le suivi des ordres, car le filtrage passe-bande ordinaire du signal converti dans le domaine de révolution (c'est-à-dire en utilisant un filtre passe-bande IIR approprié autour de l'ordre respectif) fournit alors directement les courbes d'ordre individuelles (pour plus de détails, voir RevolutionSyncSampling:

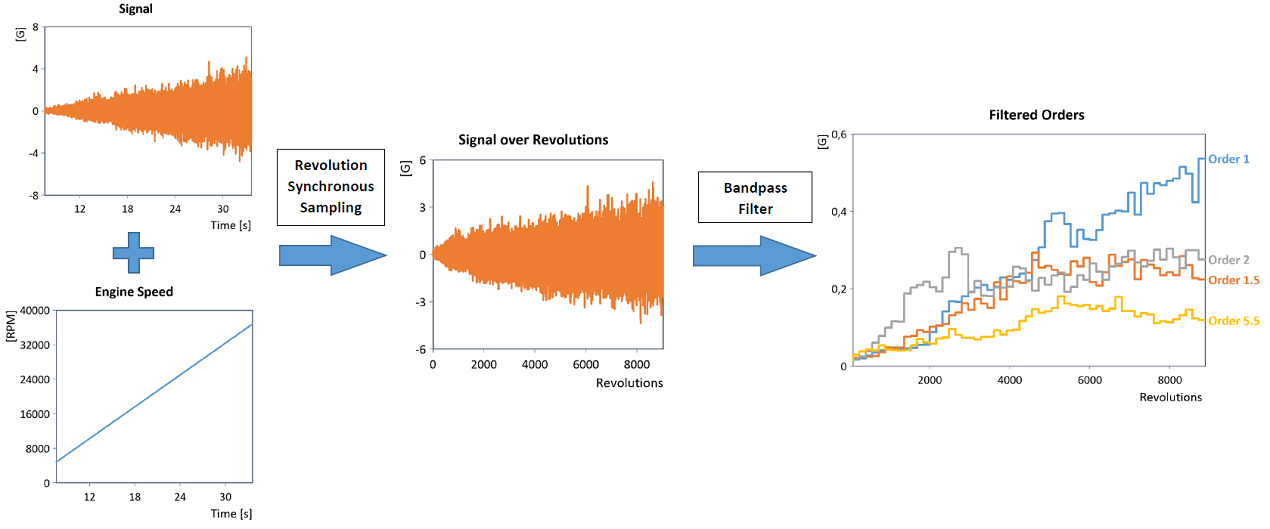
L'objet d'analyse Filtre d'ordres (contrairement à l'objet d'analyse Analyse d'ordre synchrone en révolution) permet le calcul et le retour des ordres filtrés dans le domaine temporel original. L'objet d'analyse peut donc également être utilisé pour des analyses acoustiques des ordres filtrés.

Deux méthodes de mesure sont principalement utilisées pour l'analyse d'ordre. Lors d'une montée en puissance, la vibration et la vitesse instantanée sont mesurées de manière synchrone, alors que la machine est généralement montée en puissance lentement de sa vitesse minimale à sa vitesse maximale(analyse de montée en puissance). Dans une deuxième méthode, la machine est d'abord amenée à une certaine vitesse, puis une mesure des vibrations est effectuée pour cette vitesse (analyse d'ordre avec vitesse constante). L'objet d'analyse Filtre d'ordres prend en charge les deux variantes. Le suivi d'ordre utilisant le rééchantillonnage synchrone de la révolution est également très flexible et peut même être effectué pour des ensembles de données de vitesse bruyants ou non monotones.Analyse d'ordre avec vitesse variable).

Onglet Données

Il s'agit de l'onglet où sont spécifiés les données d'entrée et les paramètres pour la transformation du domaine temporel au domaine révolutionnaire (pour plus de détails, voir également RevolutionSyncSampling) :.

Signaux dans le domaine temporel

Le signal temporel à analyser pour l'objet d'analyse doit se trouver dans la structure de données Signal. La vitesse peut être spécifiée soit dans la structure de données Signal (correspond à une analyse d'exécution avec une vitesse variable) soit comme une valeur scalaire (correspond à un suivi d'ordre avec une vitesse constante ou à une fréquence fondamentale fixe).

S'il n'y a pas d'unités ou si la gestion des unités est désactivée, la vitesse est toujours interprétée dans l'unité [1/min] (rpm) et la composante X du signal temporel est interprétée dans l'unité .

La vitesse instantanée est souvent mesurée à l'aide d'un codeur d'impulsions, qui enregistre un certain nombre d'impulsions par tour. Vous pouvez convertir le signal d'impulsion résultant directement en un signal de vitesse. Pour ce faire, sélectionnez l'option La vitesse est un signal d'impulsion et spécifiez le Nombre d'impulsions par tour. La conversion du signal d'impulsion en un signal de vitesse se fait avec la fonction ImpulseToFrequency.

Rééchantillonnage dans le domaine de révolution

Trois modes différents sont disponibles pour le rééchantillonnage du domaine temporel au domaine de révolution. Dans la plupart des applications pratiques, un rééchantillonnage linéaire est suffisant :

Si la méthode de rééchantillonnage par splines ou FFT est sélectionnée, il faut spécifier un facteur de rééchantillonnage par lequel le taux d'échantillonnage du signal est augmenté pendant l'algorithme de transformation.

Quelle que soit la méthode de rééchantillonnage choisie, le nombre de points de données par révolution pour le signal transformé dans le domaine de révolution doit être spécifié. Cela détermine l'échantillonnage du signal transformé dans le domaine de révolution. Selon le théorème d'échantillonnage de Nyquist, la moitié de la valeur détermine l'ordre maximal qui peut même être calculé.

Pour déterminer le nombre de points de données par révolution, deux modes sont disponibles :

Onglet Options

Dans cet onglet, le filtre d'ordres est spécifié pour le filtrage passe-bande d'ordres simples ou multiples. Ici, un filtrage passe-bande IIR ordinaire est effectué autour de l'ordre respectif du signal transformé dans le domaine de révolution (pour plus de détails, voir également RevolutionSyncSampling).

Résultats

Les quatre modes de résultat suivants sont disponibles pour l'objet d'analyse Filtre d'ordres :

Filtre passe-bande

Pour calculer les courbes d'ordre, un filtrage passe-bande IIR ordinaire est effectué autour de l'ordre respectif du signal transformé dans le domaine de révolution. Les filtres passe-bande suivants sont disponibles :

Ordres à filtrer

Les ordres à filtrer peuvent être explicitement définis dans un tableau ou extraits d'un ensemble de données. Les ordres sélectionnés forment la fréquence de la bande médiane du filtre passe-bande réglé. Les largeurs de bande d'ordre peuvent être exprimées symétriquement autour de l'ordre comme des largeurs de bande de filtre de 3dB. La largeur de bande du filtre 3dB définit la plage d'ordre, en dehors de laquelle les fréquences sont bloquées (définie par le point -3 dB, c'est-à-dire le point auquel 70,7 % de l'amplitude du signal original est atteint).

Calcul de la valeur RMS

Les deux modes RMS suivants sont disponibles pour calculer les courbes RMS des ordres filtrés (sous forme de liste ou de série de signaux) ou pour le calcul RMS de la somme des ordres filtrés :

Exemple d'un filtre d'ordres avec calcul de la valeur efficace par bloc pour une montée (avec Y = amplitude, X = vitesse) :

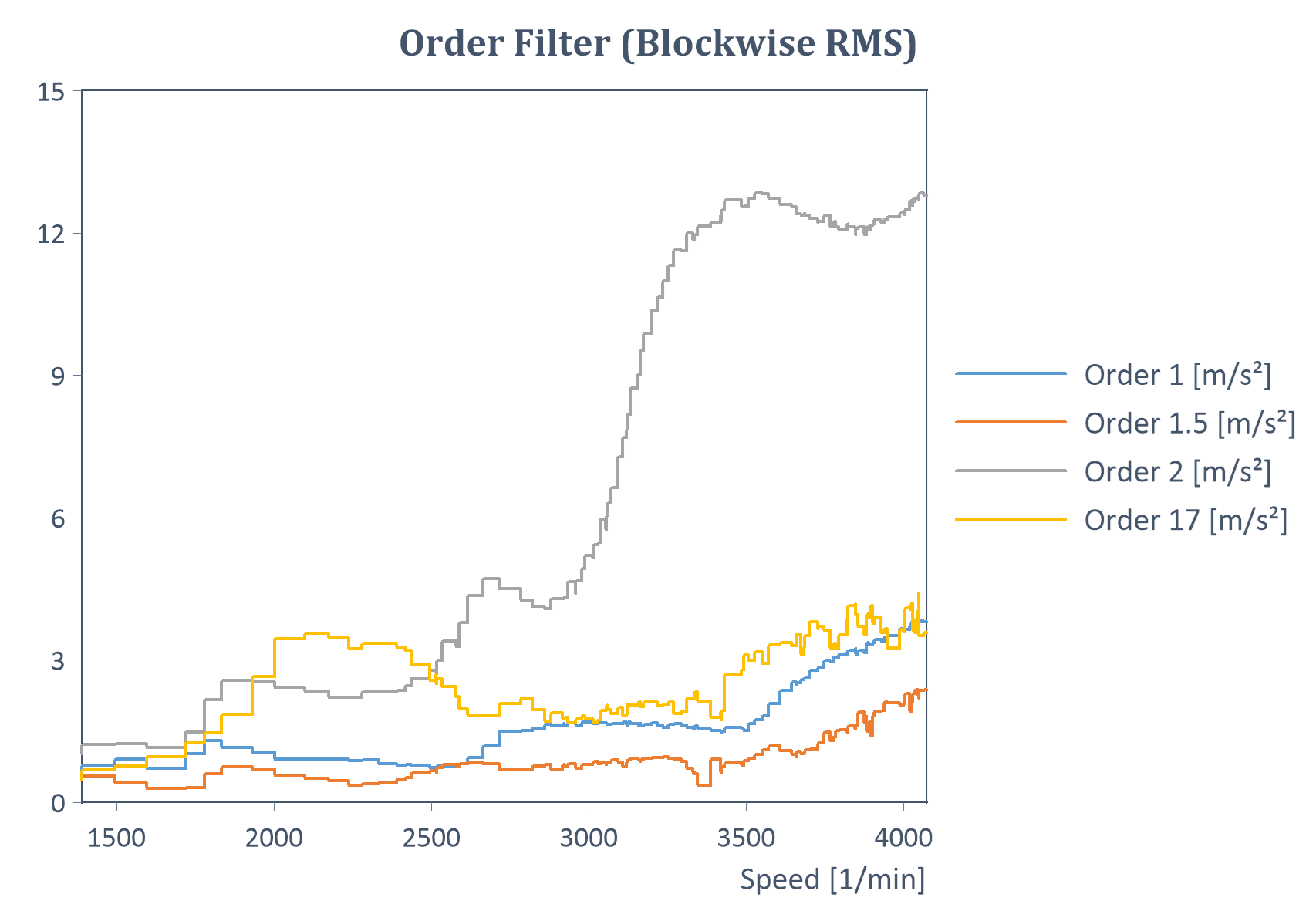
Résultat

Pour tous les modes de résultat (à l'exception de l'analyse d'ordre RMS moyennés), les types de résultats suivants sont disponibles :

Pour le résultat Y = amplitude, X = vitesse le résultat contient des points d'échantillonnage de vitesse non équidistants (ceux-ci correspondent exactement aux points d'échantillonnage de révolution équidistants après filtrage dans le domaine de révolution). Le résultat peut donc également être évalué sur une plage de vitesse équidistante, la Vitesse initiale, la Vitesse finale et l'Incrément de vitesse devant être définis. Ici, une interpolation linéaire est effectuée sur la plage de vitesse équidistante spécifiée. Pour que le rééchantillonnage linéaire donne des résultats significatifs, la résolution de vitesse calculée par l'algorithme doit être suffisamment élevée (par exemple, calcul de la valeur efficace glissante ou calcul de la valeur efficace par bloc avec une taille de bloc suffisamment petite).

Remarque : Le calcul des courbes RMS (par blocs) des ordres à filtrer fournit des courbes similaires à l'objet d'analyse Suivi des ordres synchrones de la révolution. À cette fin, dans ce dernier objet d'analyse, le mode de résultat Coupes d'ordres y compris Extraction du niveau RMS dans la bande d'ordre doit être défini. L'analyse de la moyenne des ordres RMS des deux objets d'analyse donne les mêmes résultats.

Exemple d'un filtre d'ordres à travers le temps pour une hausse (Y = amplitude, X = temps) :

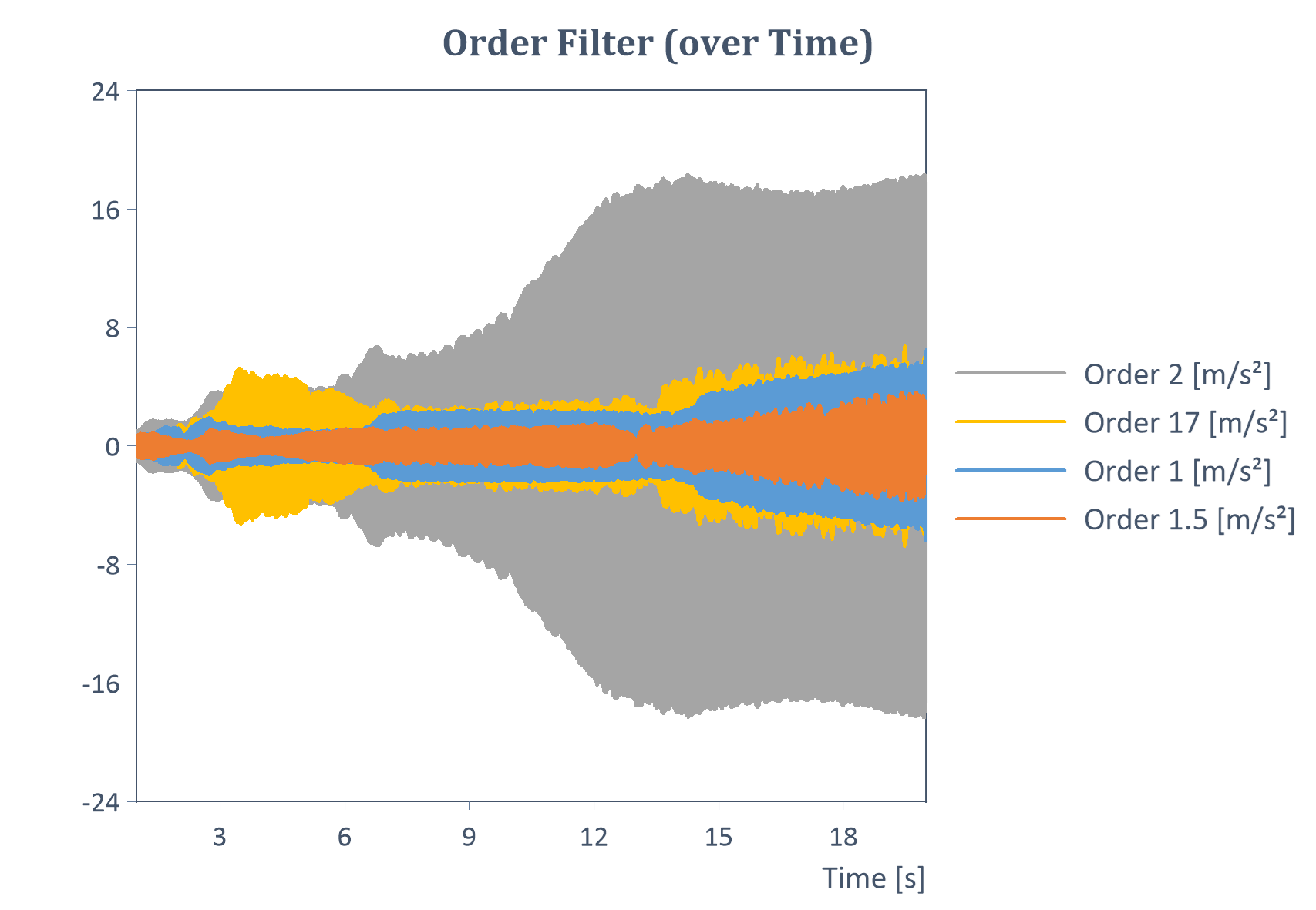
Exemple d'analyse de la moyenne des ordres RMS pour un signal à vitesse constante (RMS de chaque ordre filtré) :

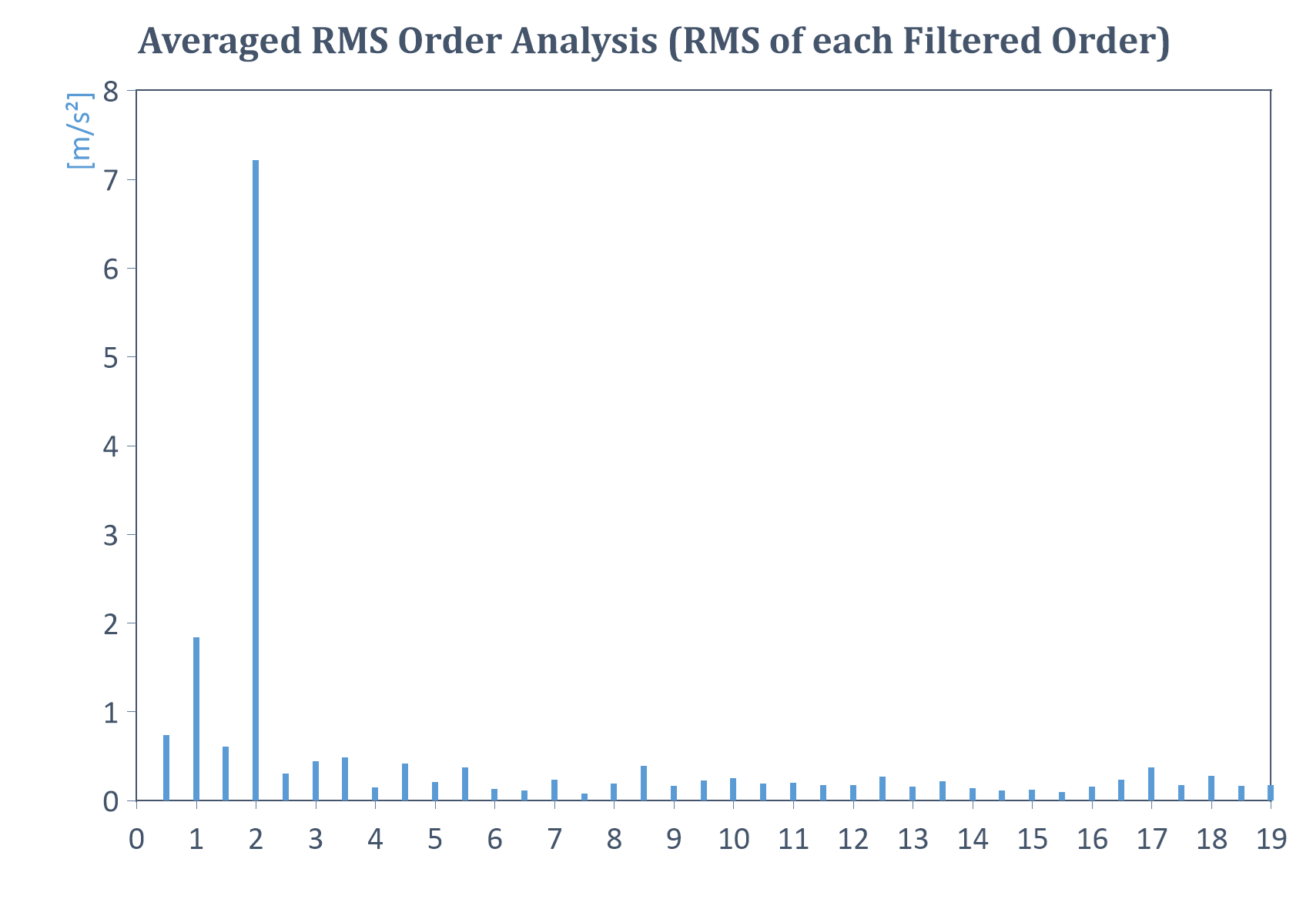
Exemples

Dans la base de données projet C:\Users\Public\Documents\Weisang\FlexPro\2021\Exemples\Analyse d'ordre.fpd ou C:>Utilisateurs>Public>Documents publics>Weisang>FlexPro>2021\Exemples\Analyse d'ordre.fpd vous trouverez des exemples des différents cas d'utilisation et modes pour lesquels une analyse d'ordre peut être effectuée. En particulier, les graphiques ci-dessus y sont inclus.

Fonctions FPScript utilisées

RevolutionSyncSampling

IIRFilter

IIRPeakFilter

ImpulseToFrequency

Voir aussi

Objets d'analyse

Option Analyse d'ordre

Objet d'analyse Analyse d'ordre synchrone en révolution

Objet d'analyse Échantillonnage synchrone en révolution

Filtre IIR

Filtre harmonique