Objet d’analyse Grandeur instantanée (Option Analyse spectrale)
Utilisez cet objet d'analyse pour déterminer les grandeurs instantanées(amplitude instantanée, phase instantanée et fréquence instantanée) des signaux. L'amplitude instantanée donne la réponse en amplitude, la phase instantanée donne la réponse en phase et la fréquence instantanée donne la réponse en fréquence du signal à analyser. Si le signal de base ne présente pas de tendance, l'amplitude instantanée correspondra également à l'enveloppe supérieure du signal.
Le calcul de la grandeur instantanée ne convient que pour les signaux à un seul composant.
Dans l'exemple suivant, l'amplitude instantanée et la fréquence instantanée d'un cosinus de fréquence balayée modulé en amplitude sont déterminées à l'aide de l' objet d'analyse Grandeur instantanée:
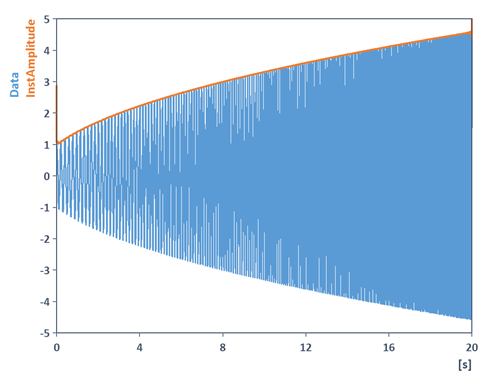
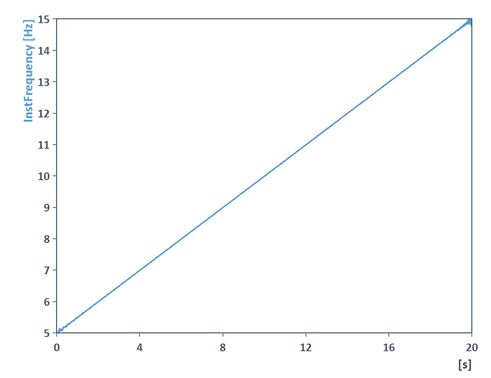
Les grandeurs instantanées peuvent donc également être utilisées pour la démodulation des signaux (démodulation d'amplitude, démodulation de phase, démodulation de fréquence). De plus amples informations sur la fonction AnalyticSignal sont disponibles dans l'aide en ligne.
Algorithme
Dans les références anglaises, ces grandeurs instantanées sont généralement décrites comme l'amplitude instantanée (ou enveloppe instantanée), la phase instantanée et la fréquence instantanée et sont calculées à l'aide de la transformée de Hilbert. De plus amples informations sur la fonction Hilbert ou la fonction AnalyticSignal sont disponibles dans l'aide en ligne.
Paramètre : Longueur FFT
La transformée de Hilbert effectue en interne une transformée de Fourier (FFT) de l'ensemble des données. En utilisant un rajout de zéro (zero padding), c'est-à-dire en sélectionnant la longueur de la FFT comme étant supérieure à la longueur des données, la résolution de la FFT requise pour l'algorithme est augmentée. Le résultat du calcul peut ainsi être amélioré. Les paramètres suivants peuvent être sélectionnés pour la longueur de la FFT dans l'objet d'analyse :
Option |
Description Longueur données |
Défini la longueur de la FFT pour qu'elle soit égale à la longueur des données. |
|---|---|---|
Puissance de 2 suivante |
Règle la longueur de la FFT pour qu'elle soit égale à la prochaine puissance de deux la plus élevée. |
|
Paramètre : Supprimer tendance
Pour les signaux présentant une tendance ou un décalage, il faut d'abord supprimer la tendance avant de trouver les grandeurs instantanées. Les options suivantes sont disponibles dans l'objet d'analyse. Les trois premières options correspondent aux options permettant de supprimer la tendance de l'objet d'analyse pour l'analyse du signal. Vous avez également la possibilité de corriger la tendance en calculant les valeurs moyennes glissantes :
Option |
Description |
|---|---|
Constante |
Soustrait la valeur moyenne de l'ensemble des données. |
Linéaire |
Soustrait la meilleure ligne droite, c'est-à-dire la ligne droite pour laquelle la somme des écarts au carré est minimale par rapport à l'ensemble des données. |
Adaptif |
Soustrait la valeur moyenne de l'enveloppe supérieure et inférieure. Ce paramètre peut être utilisé si la tendance existante n'est ni constante ni linéaire, mais dépend du temps. |
Valeur moyenne glissante |
Soustrait la valeur moyenne glissante. La valeur moyenne glissante requise pour former la largeur de l'intervalle peut être saisie. Ce paramètre peut être utilisé si la tendance existante n'est ni constante ni linéaire, mais dépend du temps. |
Filtre composante continue |
Filtre passe-haut pour éliminer l'offset DC (IIR Butterworth passe-haut). La fréquence de coupure et l'ordre (c'est-à-dire la pente) du filtre passe-haut peuvent être réglés. Le filtre peut être utilisé si la tendance actuelle n'est ni constante ni linéaire, mais dépendante du temps. |
Pour déterminer la tendance constante ou linéaire, on calcule d'abord la valeur moyenne du signal, puis on recherche le premier et le dernier franchissement de niveau à l'aide de cette valeur. Si deux passages à niveau ont été trouvés, alors la valeur moyenne ou la meilleure ligne droite est calculée uniquement pour l'intervalle entre ces deux passages à niveau. Cela permet d'éviter les erreurs qui se produisent en raison du segment de phase des signaux périodiques aux extrémités de l'ensemble de données. Si aucun passage de niveau n'a été trouvé, alors toutes les valeurs sont incluses dans le calcul. Les paramètres appropriés pour supprimer une tendance dépendant du temps sont généralement la soustraction de la moyenne glissante et le filtre de décalage DC.
Exemple et détails
Vous trouverez plus d'informations et de détails sur l'exemple ci-dessus dans l'aide en ligne traitant de la fonction AnalyticSignal.
