weisang.com > Dokumentation > Objet d’analyse Enveloppe *

Documentation FlexPro

Objet d’analyse Enveloppe *

23.08.2021

Vous pouvez utiliser cet objet d'analyse pour calculer l'enveloppe d'un ensemble de données (enveloppe supérieure et inférieure).

L'objet d'analyse peut traiter des séries de données, des matrices de données, des signaux, des séries de signaux et des listes.

Trois algorithmes sont disponibles pour calculer l'enveloppe : Pente maximale, Enveloppe Peak et Transformée de Hilbert :

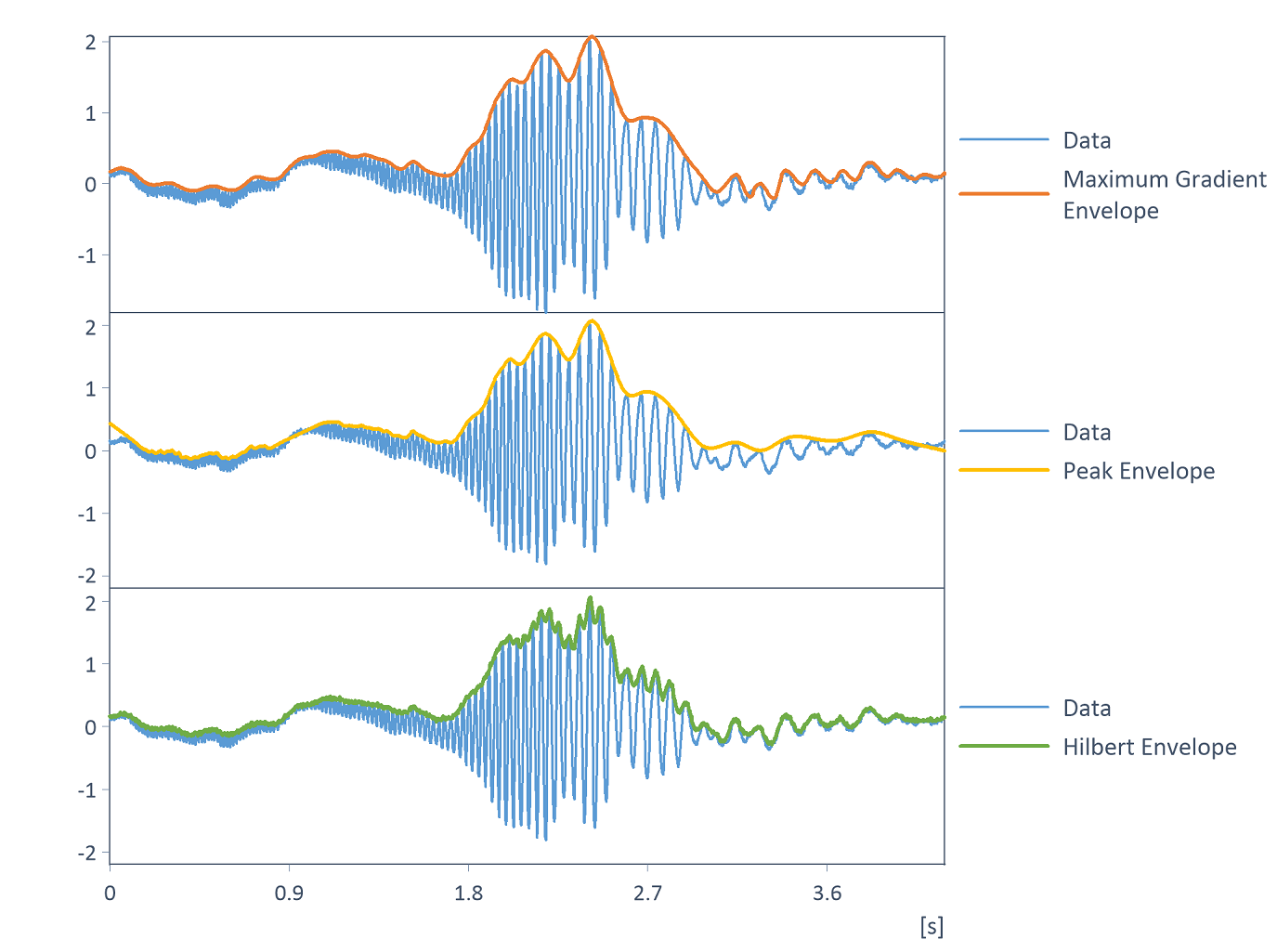
L'algorithme de la pente maximale est basé sur la fonction UpperEnvelope ou LowerEnvelope. En commençant par le premier point de données, des connexions en ligne droite sont calculées pour tous les voisins d'un intervalle et leurs pentes sont déterminées. Le voisin présentant la pente la plus élevée devient le prochain point d'échantillonnage de l'enveloppe et l'algorithme se poursuit avec cette valeur. La largeur de l'intervalle peut être calculée automatiquement ou saisie manuellement. L'enveloppe comporte donc moins de points de données que l'ensemble de données d'entrée. En utilisant l'interpolation linéaire, l'échantillonnage du résultat peut être augmenté jusqu'à l'échantillonnage de l'ensemble des données d'entrée. On peut aussi lisser les points de l'enveloppe en utilisant l'interpolation spline.

L'enveloppe Peak calcule les points de l'enveloppe comme des extrema locaux (maxima ou minima) à l'aide de la fonction Extrema. L'hystérésis peut être spécifiée pour déterminer l'extrema. L'hystérésis est la quantité minimale dont le signal doit monter ou descendre avant et après un extrême pour que le point soit accepté comme une valeur extrême. Vous pouvez spécifier l'hystérésis comme une valeur absolue ou comme un pourcentage de l'étendue de l'ensemble de données. Un autre paramètre qui peut être défini consiste à déterminer si les points limites de l'enveloppe correspondent aux points limites de l'ensemble de données d'entrée ou s'ils doivent être extrapolés. Comme pour l'algorithme de la pente maximale, l'échantillonnage du résultat peut être augmenté jusqu'à l'échantillonnage de l'ensemble des données d'entrée en utilisant une interpolation linéaire ou l'enveloppe peut être lissée en utilisant une interpolation spline.

L'algorithme de la transformée de Hilbert calcule l'enveloppe à l'aide de la transformée de Hilbert. On obtient ainsi une définition mathématiquement exacte des enveloppes comme étant la valeur absolue du signal analytique calculé par la transformée de Hilbert (voir aussi Calcul du signal analytique). La transformation de Hilbert effectue en interne une transformation de Fourier (FFT) de l'ensemble des données. En utilisant un rajout de zéro (zero padding), c'est-à-dire en sélectionnant la longueur de la FFT comme étant supérieure à la longueur des données, la résolution de la FFT requise pour l'algorithme est augmentée. Le résultat du calcul peut ainsi être amélioré. Dans l'objet d'analyse, la longueur de la FFT peut donc être augmentée jusqu'à la puissance de deux suivante si nécessaire. Pour les signaux qui ont une tendance ou un décalage, la tendance doit également être supprimée au préalable afin de déterminer les enveloppes à l'aide de la transformée de Hilbert. Les options fournies ci-dessous correspondent aux options disponibles pour Analyse du signal - Objet d'analyse suppression de la tendance :

Sélection	Signification
Constante	Soustrait la valeur moyenne de l'ensemble des données.
Linéaire	Soustrait la meilleure ligne droite, c'est-à-dire la ligne droite pour laquelle la somme des carrés des écarts à l'ensemble des données est minimale.
Adaptif	Soustrait la valeur moyenne de l'enveloppe supérieure et inférieure. Ce paramètre peut être utilisé si la tendance actuelle n'est ni constante ni linéaire, mais dépend du temps.
Moyenne glissante	Soustrait la moyenne glissante. La largeur de l'intervalle nécessaire à la formation de la moyenne glissante peut être saisie. Ce paramètre peut être utilisé si la tendance actuelle n'est ni constante ni linéaire, mais dépend du temps. Le filtre à moyenne glissante est un filtre passe-haut.
Filtre composante continue	Filtre passe-haut pour éliminer l'offset DC (IIR Butterworth passe-haut). La fréquence de coupure et l'ordre (c'est-à-dire la pente) du filtre passe-haut peuvent être configurés. Le filtre peut être utilisé si la tendance actuelle n'est ni constante ni linéaire, mais dépendante du temps.

Les options de paramétrage appropriées pour supprimer une tendance dépendant du temps sont généralement la soustraction de la moyenne glissante et le filtre composante continue.