Vous pouvez utiliser cet objet d'analyse pour effectuer une interpolation spline de vos données, c'est-à-dire pour calculer une courbe lisse qui relie les points de votre ensemble de données. L'interpolation Spline est directement intégrée dans le tracé de ligne de FlexPro, de sorte que vous n'utilisez cet objet d'analyse que lorsque vous souhaitez traiter mathématiquement des données lissées.

Avec l'interpolation par spline, tous les points voisins de la courbe sont reliés par des polynômes du troisième degré, c'est-à-dire des fonctions de la forme :

Deux polynômes se rencontrent à chaque point de la courbe. Le premier et le dernier point de la courbe constituent l'exception. Les coefficients ai, bi, ci et di des polynômes sont choisis de telle sorte que les polynômes voisins concordent en termes de lieu, de gradient et de courbure aux endroits où ils se rencontrent. Pour le premier et le dernier point où aucun polynôme ne se rencontre, vous pouvez modifier l'apparence de la courbe spline en utilisant ce que l'on appelle des conditions aux limites, c'est-à-dire que vous spécifiez le gradient ou la courbure de la courbe spline aux bords gauche et droit. Selon le type de conditions aux limites, vous obtenez une apparence différente de la courbe spline, comme le montre l'illustration suivante :

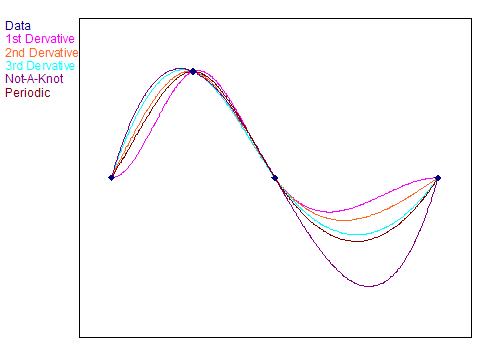
Cela met en évidence :

•Splines naturelles. Vous les obtenez lorsque vous sélectionnez Courbures comme spécifié comme condition aux limites et que vous saisissez la valeur zéro pour les valeurs des courbures aux deux bords. L'aspect correspond à la courbe que vous obtiendriez si vous reliiez les points de la courbe à l'aide d'une règle en caoutchouc.

•Spline compensatrice. La courbe calculée de cette manière ne passe pas nécessairement par les points d'échantillonnage spécifiés. L'ondulation de la courbe peut être contrôlée à l'aide d'un facteur de pondération. Si le facteur de pondération est proche de zéro, la courbe spline donne la meilleure ligne droite par rapport à l'erreur quadratique. Pour un très grand facteur de pondération, on obtient une courbe spline naturelle, qui correspond aux conditions limites spécifiées ci-dessus. Dans ce cas le tracé de la courbe spline suit les points de la courbe.

•Les splines périodiques proviennent de l'exigence selon laquelle la courbe de la spline doit correspondre en termes de gradient et de courbure aux bords gauche et droit. Vous pouvez ensuite superposer les courbes splines résultantes plusieurs fois de suite, sans que des plis ne se forment au niveau des joints. Pour calculer une interpolation par spline périodique, les valeurs Y du premier et du dernier point doivent être les mêmes. Si ce n'est pas le cas, FlexPro utilise l'une des deux méthodes suivantes pour forcer la périodicité. Si vous sélectionnez Périodique, périodicité par remplacement, la dernière valeur Y de l'ensemble de données est ignorée et une copie de la première valeur Y est utilisée à la place. Toutefois, si vous sélectionnez Périodique, périodicité par ajout, une copie de la première valeur Y est ajoutée à l'ensemble de données si la dernière valeur Y de l'ensemble de données n'est pas identique à la première. La valeur X du dernier point original plus la différence entre la dernière et l'avant-dernière valeur X est utilisée comme valeur X pour ce point supplémentaire.

•Splines avec une condition limite "Not-A-Knot". Ceux-ci utilisent deux polynômes identiques, l'un sur le bord gauche et l'autre sur le bord droit, ce qui correspond à la condition que la troisième dérivée des fonctions Spline dans le deuxième et l'avant-dernier point de données soit continue. Cela signifie que ces points ne sont pas de véritables points nodaux sur la courbe spline.

La condition préalable à l'interpolation par spline est que les valeurs X des points soient strictement croissantes. Si ce n'est pas le cas (par exemple, avec une courbe de locus), vous devez alors utiliser l'interpolation spline paramétrique. Les valeurs X, cependant, ne doivent pas être équidistantes. Après le calcul des coefficients de la courbe spline, FlexPro peut évaluer la fonction spline calculée en tout point pour obtenir de nouveaux points d'échantillonnage.

L'illustration suivante montre des splines de compensation avec différents facteurs de pondération :

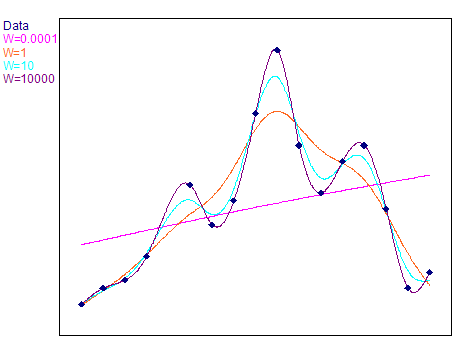
Le résultat de l'interpolation par spline est d'abord un modèle mathématique de l'ensemble des données à interpoler. Lemode d'évaluation spécifie les points sur lesquels la courbe spline calculée doit être évaluée pour obtenir l'ensemble de données de résultat. Les modes d'évaluation suivants sont possibles :

•N-valeurs équidistantes: Dans ce cas, la courbe spline est évaluée à N points d'échantillonnage équidistants, quelle que soit la façon dont les valeurs X ont été précédemment distribuées.

•N-valeurs par intervalle X: Dans ce cas, chaque intervalle X précédent est divisé en N intervalles de taille égale, aux limites desquels la fonction spline est évaluée.

L'illustration suivante montre le fonctionnement des deux modes d'évaluation :

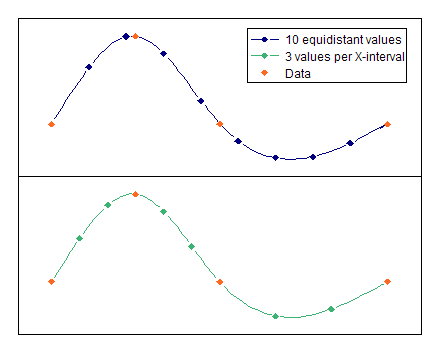
Fonctions FPScript utilisées

Spline

CompensatingSpline

PeriodicSpline

Voir aussi

Objet d'analyse Interpolation paramétrique Spline

Objet d'analyse Interpolation linéaire

* Cet objet d'analyse n'est pas disponible dans FlexPro View.