weisang.com > Dokumentation > Objet d’analyse Échantillonnage synchrone en révolution (Option Analyse d’ordre)

Documentation FlexPro

Objet d’analyse Échantillonnage synchrone en révolution (Option Analyse d’ordre)

23.04.2021

L'objet d'analyse Échantillonnage synchrone en révolution transforme un signal échantillonné dans le temps dans le domaine de révolution. Le signal n'est alors plus disponible par pas temporels équidistants, mais par pas d'angles de rotation équidistants (c'est-à-dire par intervalles de rotation équidistants). Dans la littérature de référence, on parle d'échantillonnage angulaire synchrone, de suivi d'ordre calculé, d'échantillonnage synchrone ou même de rééchantillonnage adaptatif.

Il s'agit d'une méthode efficace pour effectuer l'analyse d'ordre, puisque le spectre de fréquence (c'est-à-dire la transformée de Fourier) du signal converti dans le domaine de révolution fournit directement le spectre d'ordre :

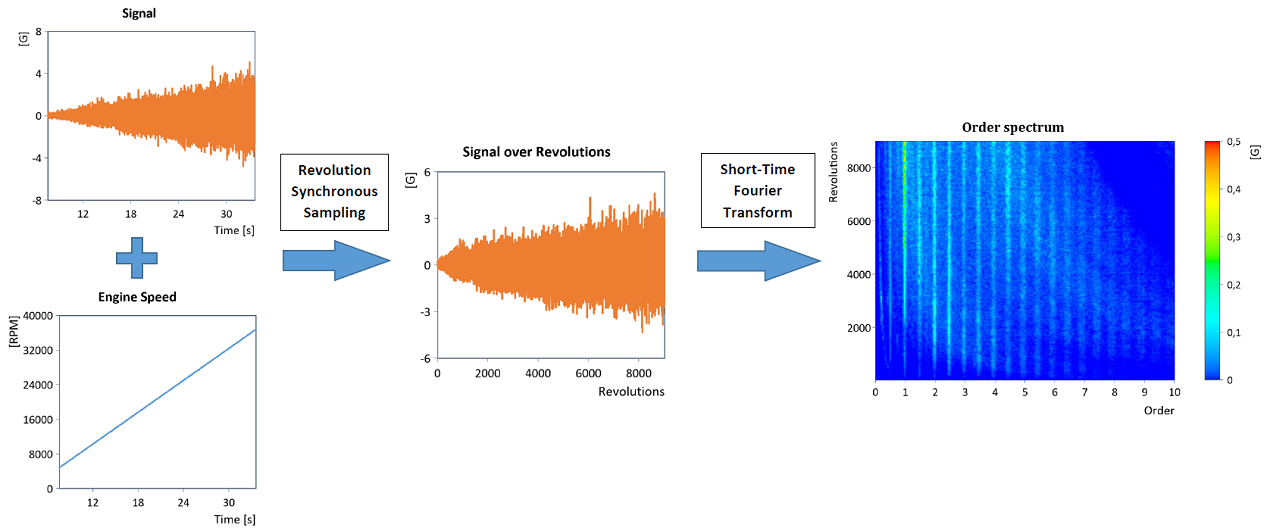
De la même manière, un filtrage passe-bande ordinaire (par exemple, en utilisant un filtre passe-bande IIR approprié) peut être utilisé pour déterminer la courbe des ordres individuels dans le domaine de révolution (on voit ici la courbe RMS par blocs des ordres filtrés) :

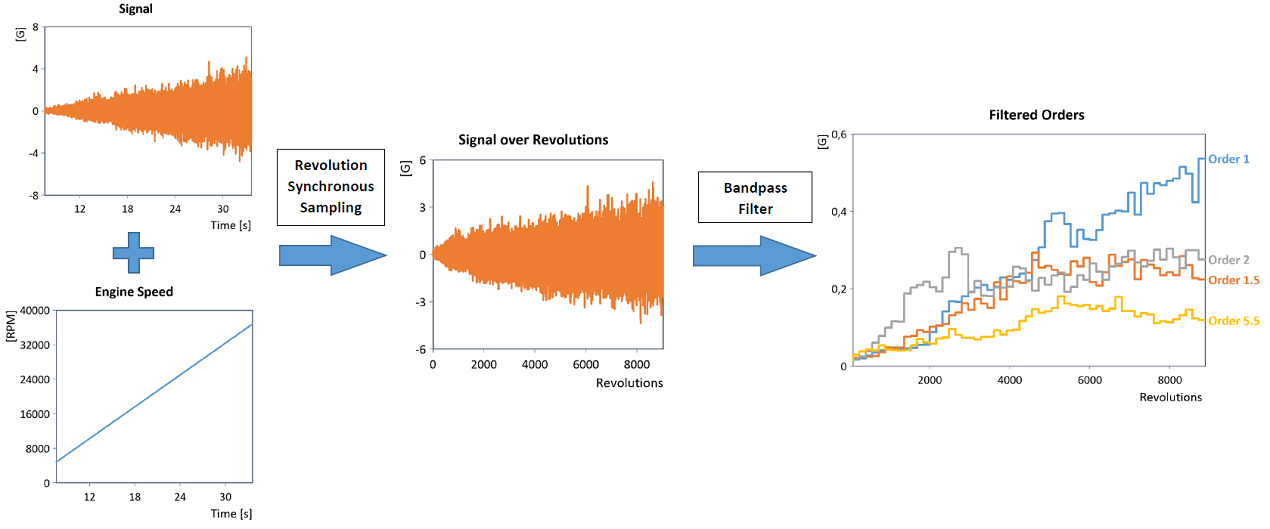
Remarque : l'analyse de Fourier dans le domaine de révolution (par exemple, le calcul d'un spectre d'ordre) ainsi que le filtrage passe-bande dans le domaine de révolution peuvent être effectués directement en une seule étape avec les objets d'analyse Analyse d'ordre synchrone en révolution et Filtre d'ordres.

Onglet Données

Cet onglet spécifie les données d'entrée dans le domaine temporel (pour plus d'informations, voir également RevolutionSyncSampling) :

Signaux dans le domaine temporel

Le signal temporel à analyser pour l'objet d'analyse doit se trouver dans la structure de données Signal. La vitesse peut être stockée dans la structure de données Signal (correspond à la vitesse de démarrage ou variable) ou comme une valeur scalaire (correspond à la vitesse constante ou à la fréquence fondamentale).

S'il n'y a pas d'unités ou si la gestion des unités est désactivée, la vitesse est toujours interprétée dans l'unité [1/min] et la composante X du signal temporel est interprétée dans l'unité .

La vitesse instantanée est souvent mesurée à l'aide d'un codeur d'impulsions, qui enregistre un certain nombre d'impulsions par tour. Vous pouvez convertir le signal d'impulsion résultant directement en un signal de vitesse. Pour ce faire, sélectionnez l'option La vitesse est un signal impulsionnel et spécifiez le Nombre d'impulsions par tour. La conversion du signal d'impulsion en un signal de vitesse se fait avec la fonction ImpulseToFrequency.

Onglet Options

C'est dans cet onglet que sont spécifiés les paramètres de transformation du domaine temporel au domaine de révolution. Schématiquement, l'algorithme du processus de transformation peut être décrit comme suit (pour plus d'informations, voir également RevolutionSyncSampling) :

Rééchantillonnage dans le domaine de révolution

Trois modes différents sont disponibles pour le rééchantillonnage du domaine temporel au domaine de révolution. Dans la plupart des applications pratiques, le rééchantillonnage linéaire est suffisant :

Méthode de rééchantillonnage	Description
Interpolation linéaire	Le signal temporel est évalué aux points temporels (non équidistants) des points d'échantillonnage de révolution équidistants au moyen d'une interpolation linéaire avant d'être transformé dans le domaine de révolution. Cela rend la transformation rapide, mais peut provoquer un aliasing dans l'analyse FFT ultérieure du signal échantillonné synchrone basé sur la révolution.
Interpolation spline	Le signal temporel est évalué aux points temporels (non équidistants) des points d'échantillonnage de révolution équidistants au moyen d'une interpolation spline avant d'être transformé dans le domaine de révolution. Par rapport au rééchantillonnage linéaire, l'interpolation spline est légèrement plus lente, mais l'aliasing est réduit.
Rééchantillonnage FFT	Le signal temporel est évalué par rééchantillonnage FFT aux points temporels (non équidistants) des points d'échantillonnage de révolution équidistants avant d'être transformé dans le domaine de révolution. Ici, le signal temporel est d'abord transformé dans le domaine fréquentiel, où des zéros sont ajoutés, puis retransformé dans le domaine temporel. Le rééchantillonnage au moyen de la transformée de Fourier conduit à un résultat presque idéal, car il n'ajoute aucune composante de signal à haute fréquence. Les effets d'alias dans le calcul du spectre d'ordre sont presque absents, mais le temps de calcul augmente significativement.

Si la méthode de rééchantillonnage par splines ou FFT est sélectionnée, il faut spécifier un facteur de rééchantillonnage par lequel le taux d'échantillonnage du signal est augmenté pendant l'algorithme de transformation.

Quelle que soit la méthode de rééchantillonnage choisie, le nombre de points de données par révolution pour le signal transformé dans le domaine de révolution doit être spécifié. Cela détermine l'échantillonnage du signal transformé dans le domaine de révolution. Selon le théorème d'échantillonnage de Nyquist, la moitié de la valeur détermine l'ordre maximal qui peut même être calculé à l'aide de l'analyse de Fourier.

Pour déterminer le nombre de points de données par révolution, deux modes sont disponibles :

Points de données par révolution	Description
Automatique (adaptation à l'ordre max.)	Calcule une valeur automatique pour le nombre de points de données par tour afin que l'ordre théoriquement le plus grand apparaissant dans le signal puisse encore être calculé à l'aide de l'analyse de Fourier. La valeur calculée automatiquement peut être limitée par une valeur limite librement ajustable.
Valeur fixe	Pour le nombre de points de données par tour, toute valeur fixe peut être spécifiée.

Détermination de la tendance dans le domaine de révolution

Dans de nombreux exemples d'application, un décalage en courant continu existant et excessivement important conduit à une représentation visuellement inadaptée dans le tracé des contours du spectre d'ordre, dans lequel la composante en courant continu domine. Il est donc avantageux de filtrer la composante continue. À cette fin, pour le signal transformé dans le domaine de révolution, un filtre passe-haut à décalage DC correspondant avec une fréquence de coupure (ordre de coupure) et un ordre de filtre (pente du filtre ) réglables est défini (pour plus de détails sur le filtre passe-haut à décalage DC, voir la fonction DCRemovalFilter ).

Résultat dans le domaine de révolution

Le signal transformé dans le domaine de révolution, l'ensemble des données de vitesse transformé dans le domaine de révolution ou la composante temporelle transformée dans le domaine de révolution peuvent être renvoyés. Toutes les combinaisons de ces options de résultat sont également autorisées, qui sont ensuite combinées dans la structure de données liste.

Exemples

Dans la base de données projet C:\Users\Public\Documents\Weisang\FlexPro\2021\Exemples\Analyse d'ordre.fpd ou C:>Utilisateurs>Public>Documents publics>Weisang>FlexPro>2021\Exemples\Analyse d'ordre.fpd vous trouverez des exemples des différents cas d'utilisation et modes pour lesquels une analyse d'ordre peut être effectuée. En particulier, les graphiques ci-dessus y sont inclus.