HarmonicRemovalFilter (FPScript)
Supprime les composantes harmoniques des signaux temporels (suppression des harmoniques). Pour ce faire, les données sont converties du domaine temporel au domaine des révolutions, où le calcul de la moyenne et la soustraction des cycles assurent la suppression des harmoniques souhaitée.
Syntaxe
HarmonicRemovalFilter(Signal, SpeedOrFundamentalFrequency, [ OrderForHarmonicRemoval = 1 ], [ NumberOfCyclesForAveraging = 15 ], [ SamplesPerRevolution = 512 ] [ , OutputOptions = HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_TIME_DOMAIN ])
La syntaxe de la fonction HarmonicRemovalFilter se compose des éléments suivants :
Section |
Description |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Signal |
Le signal échantillonné dans le temps dont les composantes harmoniques (harmoniques) doivent être retirées. L'unité de la composante X doit être compatible avec l'unité des secondes (avec le contrôle des unités activé). Si aucune unité de la composante X n'est spécifiée ou si le contrôle des unités est désactivé, l'unité est toujours interprétée en secondes. Les structures de données autorisées sont Signal. Tous les types de données réels sont autorisés, sauf Valeur booléenne, Temps calendaire et Période de temps. Les valeurs invalides ne sont pas autorisées dans cet argument. Des restrictions supplémentaires s'appliquent à la composante X.Les valeurs doivent être monotonement croissantes. Les valeurs invalides ne sont pas autorisées dans cet argument. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||||||
SpeedOrFundamentalFrequency |
La composante rotative sous-jacente pour l'élimination des harmoniques en tant que signal de vitesse échantillonné dans le temps (à partir duquel le domaine de révolution pour l'élimination des harmoniques est dérivé). Alternativement, il s'agit de la fréquence fondamentale fixe sous-jacente. L'unité de la composante Y doit être compatible avec l'unité 1/min (ou avec RPM = tours par minute) (lorsque la gestion des unités est activée). Si aucune unité de la composante Y n'est spécifiée ou si la gestion des unités est désactivée, l'unité est toujours interprétée comme 1/min. L'unité de la composante X doit être compatible avec l'unité des secondes (avec la gestion des unités activée). Si aucune unité de la composante X n'est spécifiée ou si la gestion des unités est désactivée, l'unité est toujours interprétée en secondes. La fréquence d'échantillonnage ne doit pas nécessairement correspondre à la fréquence d'échantillonnage de Signal. S'il s'agit d'une valeur scalaire, on suppose que le signal à filtrer a été enregistré à cette vitesse constante ou que les composantes harmoniques liées à des multiples de cette fréquence fondamentale fixe doivent être extraites. Les structures de données autorisées sont Scalaire et Signal. Tous les types de données réels sont autorisés, sauf Valeur booléenne, Temps calendaire et Période de temps. L'argument est transformé dans l'unité min^-1. Les valeurs invalides ne sont pas autorisées dans cet argument. Des restrictions supplémentaires s'appliquent à la composante X.Les valeurs doivent être monotonement croissantes. Les valeurs invalides ne sont pas autorisées dans cet argument. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||||||
OrderForHarmonicRemoval |
Définit l'ordre (c'est-à-dire les multiples de la vitesse ou les multiples de la fréquence fondamentale) à supprimer du signal temporel avec toutes les composantes harmoniques. Par exemple, choisir 4 signifie que les ordres 4, 8, 12, 16, 20, etc. sont supprimés. Les structures de données autorisées sont Scalaire. Tous les types de données numériques sont autorisés. La valeur doit être supérieure à 0. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut 1 . |
||||||||||
NumberOfCyclesForAveraging |
Pour l'élimination des harmoniques, le signal à filtrer est d'abord transformé dans le domaine de révolution, où l'on effectue la moyenne et la soustraction des cycles glissants. Cette valeur détermine le nombre de cycles à moyenner dans le domaine des révolutions afin de calculer l'ordre respectif des harmoniques moyennées. Plus la valeur est grande, plus la sélectivité du filtre est importante. Les structures de données autorisées sont Scalaire. Tous les types de données entiers sont autorisés. La valeur doit être supérieure ou égale à 2. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut 15 . |
||||||||||
SamplesPerRevolution |
Pour l'élimination des harmoniques, le signal à filtrer est d'abord transformé dans le domaine de révolution. Cette valeur détermine l'échantillonnage du signal transformé dans le domaine de révolution (nombre de points de données par révolution). La moitié de la valeur détermine l'ordre maximal qui peut même être calculé à l'aide de l'analyse de Fourier selon le théorème d'échantillonnage. Il convient donc de choisir une valeur telle que tous les ordres supérieurs à la moitié de cette valeur soient négligeables. Sinon, il y a aliasing (selon le théorème d'échantillonnage). Les valeurs plus petites, en revanche, réduisent le temps de calcul de l'algorithme. La valeur doit également être définie de manière à ce que SamplesPerRevolution / OrderForHarmonicRemoval soit un nombre entier. Si cette dernière condition n'est pas remplie, des valeurs approximatives pour le nombre de points de données par tour et l'ordre à filtrer sont automatiquement calculées, qui remplissent cette condition. La valeur approximative calculée par l'algorithme pour l'ordre à filtrer correspond alors à OrderForHarmonicRemoval sauf à au moins 2 décimales près. La valeur approximative calculée par l'algorithme pour le nombre de points de données par tour dans ce cas est limitée à la baisse par la valeur de SamplesPerRevolution. Les structures de données autorisées sont Scalaire. Tous les types de données entiers sont autorisés. La valeur doit être supérieure ou égale à 1. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut 512 . |
||||||||||
OutputOptions |
Précise les résultats qui doivent être renvoyés. Les résultats multiples sont renvoyés sous forme de liste. Si, par exemple, le signal filtré dans le domaine de la révolution (sans harmoniques) ainsi que le signal temporel filtré retransformé dans le domaine temporel doivent être sortis, alors l'argument doit contenir la valeur HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_REVOLUTION_DOMAIN + HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_TIME_DOMAIN. L'argument OutputOptions peut avoir les valeurs suivantes :
Si l'argument n'est pas spécifié, il est défini à la valeur par défaut HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_TIME_DOMAIN . |
Remarques
L'algorithme de la procédure de transformation peut être décrit schématiquement comme suit (par exemple, voir [1], [2], ou [3]) :
1) Transformation dans le domaine de révolution: D'abord Signal est transformé du domaine temporel au domaine de révolution (de manière analogue à la procédure de la fonction RevolutionSyncSampling où l'on choisit ici une transformation linéaire). Le domaine de révolution est calculé ici notamment à partir de l'argument SpeedOrFundamentalFrequency. De plus, la transformation nécessite des arguments nécessaires à la fonction RevolutionSyncSampling en ce qui concerne le nombre de points de données par révolution.
2) Moyenne du cycle: Dans le domaine de la révolution, une moyenne (glissante) est calculée sur un nombre de cycles défini par l'utilisateur. Tout ce qui tourne en synchronisation avec l'onde est une harmonique qui est incluse dans ce cycle de moyennes. Les composantes qui tournent de manière non synchrone avec l'onde de premier ordre sont éliminées. Par conséquent, le cycle moyen est constitué de données synchrones et harmoniques avec le tachymètre sous-jacent (c'est-à-dire avec SpeedOrFundamentalFrequency). Dans un moteur à quatre temps, par exemple, il y a un événement de combustion pour deux révolutions du vilebrequin. Un cycle est donc constitué de 2 révolutions. Si l'événement de combustion, y compris les composantes harmoniques, doit être supprimé ici, alors OrderForHarmonicRemoval doit être définit à la valeur 0,5.
3) Soustraction de cycle: Le cycle moyen (glissant) est ensuite soustrait de chaque cycle afin d'effectuer l'élimination des harmoniques souhaitée. Le résultat est alors le signal filtré dans le domaine de la révolution (sans les harmoniques de l'ordre filtré).
4) Transformation dans le domaine temporel: Le signal filtré dans le domaine de révolution est ensuite retransformé dans le domaine du temps.
A titre d'exemple, considérons le spectre d'ordre d'un signal temporel calculé à partir d'un run-up :
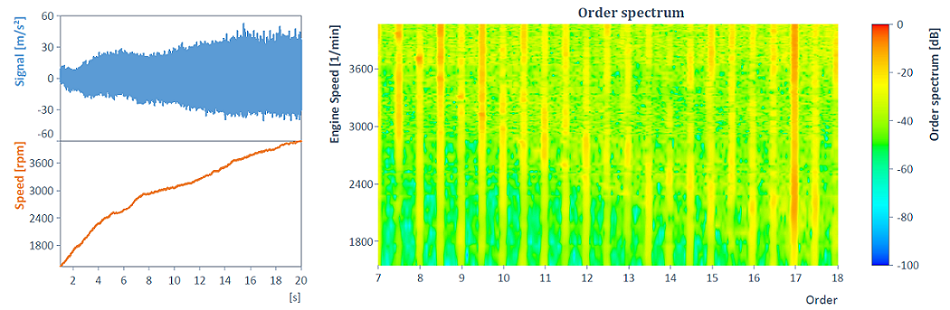
Par exemple, avec l'aide de la fonction HarmonicRemovalFilter, l'ordre 8,5 peut être supprimé avec tous les composants harmoniques :
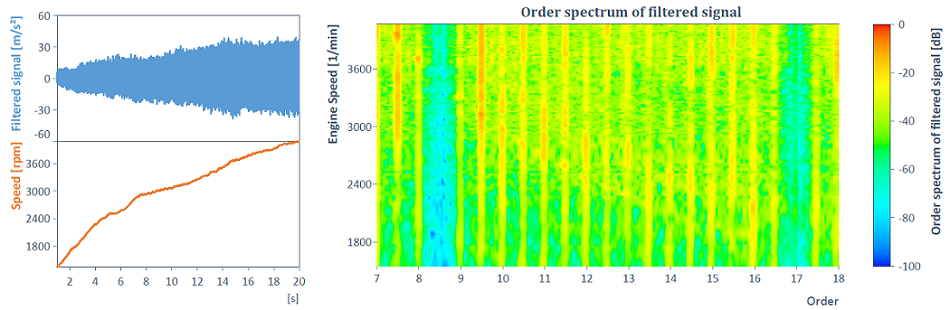
Si le résultat est une liste, il est possible d'accéder aux résultats avec les noms d'éléments de liste suivants :
Constante |
Description |
|---|---|
.["Signal_over_Time"] |
Le signal filtré (sans harmoniques) retransformé dans le domaine temporel d'origine. |
.["Signal_over_Revolutions"] |
Le signal filtré (sans harmoniques) transformé dans le domaine de révolution. |
.["Speed_over_Revolutions"] |
Le signal de vitesse transformé dans le domaine de révolution. |
.["Time_over_Revolutions"] |
Les points temporels (non équidistants) associés aux points d'échantillonnage de la révolution. |
Vous pouvez aussi toujours utiliser la syntaxe Formulaname.Listelementname.
Remarque Selon le théorème de l'échantillonnage, théoriquement tous les ordres jusqu'à orderMax = 0.5*SamplingRate(Signal)/Maximum(Speed) peuvent être détectés et analysés. SamplesPerRevolution doit être fixée à une valeur supérieure au double de la valeur de orderMax.
Disponible dans
Option Analyse d'ordre
Exemples
HarmonicRemovalFilter(Signal, Speed, 8.5)
Supprime le 8.5ème ordre (lié au signal de vitesse) ainsi que toutes les composantes harmoniques. Le résultat est le signal filtré dans le domaine temporel (sans les harmoniques correspondants)
HarmonicRemovalFilter(Signal, 12 Hz, 1)
Supprime la fréquence fondamentale de 12 Hz et ses composantes harmoniques dans un signal. Le résultat est le signal filtré dans le domaine temporel.
Dim SyncSampling = RevolutionSyncSampling(Signal, Speed, 512,,,,REVSYNCSAMPLING_OUTPUT_ALL) // Step 1: transform to rev. domain
Dim n = 512/4
Dim cycles = Reshape(SyncSampling.["Signal_over_Revolutions"], {NumberOfRows(SyncSampling.["Signal_over_Revolutions"])/n, n})
Dim avgeragedCycles = Mean(cycles, MEAN_ARITHMETIC + PROCESS_ROWS + CALC_MOVING, 25) // Step 2: cycle averaging
Dim harmonicRemoval = Signal(Reshape(cycles - avgeragedCycles), SyncSampling.["Time_over_Revolutions"]) // Step 3: cycle substraction
RemoveVoidValues(Sample(harmonicRemoval, Signal.X)) // step 4: transform back to time domain
Code FPScript équivalent à HarmonicRemovalFilter(Signal, Speed, 4, 25, 512).
Voir aussi
Fonction RevolutionSyncSampling
Objet d'analyse Filtre harmoniques
Objet d'analyse Analyse d'ordre révolution synchrone
Objet d'analyse Échantillonnage Révolution Synchrone
Littérature
[1] B. Peeters, B. Cornelis, K. Janssens, H. Van der Auweraer: Removing disturbing harmonics in Operational Modal Analysis. Dans: Proceedings of the International Operational Modal Analysis Conference IOMAC, Copenhagen, Denmark. 2007.
[2] R.B. Randall: State of the art in monitoring rotating machinery. Dans: Proceedings of the International Seminar on Modal Analysis ISMA, Leuven, Belgium. 2002.
[3] E. Bechhoefer, M. Kingsley: A Review of Time Synchronous Average Algorithms. Dans: Proceedings of the Annual Conference of the Prognostics and Health Management Society, San Diego, USA. 2009.
Vous serez probablement intéressé par les articles suivants :
Vous êtes actuellement en train de consulter le contenu d'un espace réservé de Facebook. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous devez charger le contenu de reCAPTCHA pour soumettre le formulaire. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de Instagram. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de X. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informations