Produces a two-dimensional grid. Helpful for three-dimensional visualization of functions with two variables or functions with complex-valued arguments.

Syntax

MeshGrid(X, Z)

The syntax of the MeshGrid function consists of the following parts:

Remarks

The result always has the data structure list.

From two data series, X with length N and Z with length M, the function produces a list with two entries bearing the same names: X and Z. However, the resulting entries in the list are now matrices consisting of N rows and M columns, which are formed by replicating the function arguments X or Z. The units of the result matrices match the units of the individual arguments.

The result can be interpreted as a two-dimensional rectangular grid with N x M grid points as follows: For example, specified are the data series X as {1, 2, 3, 4} in the horizontal direction and the data series Z as {7, 8, 9} in the vertical direction. The grid spanning from X and Znow comprises the coordinates (1, 7), (2, 7), (3, 7), (4, 7), ..., (1, 9), (2, 9), (3, 9), (4, 9):

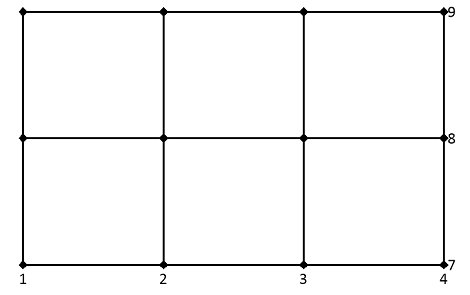
The coordinates of the individual grid points are obtained on a per-element basis from the two matrices bearing the same names:

The function MeshGrid applied to the two data series, now results in the list consisting of the matrices bearing the same name X (first list element) and Z (second list element).

The function is usually used for the three-dimensional display of the functions y = f(x, z) of two variables over a two-dimensional rectangular grid. In particular, functions y = f(z) = f(z1, z2) with complex-valued arguments z = z1 + i * z2 can be calculated and displayed over the complex plane.

Available in

FlexPro Basic, Professional, Developer Suite

Examples

Dim x = {1, 2, 3, 4}
Dim z = {7, 8, 9}
Dim grid = MeshGrid(x, z)
Dim y = grid.["X"]^2 - grid.["Z"] // = grid.[0]^2 - grid.[1]
Signal(y, x, z)

Example 1: Procedure for calculating functions with two variables

Calculates the function y = x^2 - z spanning the grid using the data series {1, 2, 3, 4} (in the X direction) and {7, 8, 9} (in the Z direction):

Dim x = Series(-4, 4, 0.01)
Dim z = x
Dim grid = MeshGrid(x, z)
Dim y = ArcTan2(grid.["Z"], grid.["X"])
Signal(y, x, z)

Example 2: Visualization of the ArcTan2 function with 2 variables

Calculates the ArcTan2 function y = f(x, z) = ArcTan2(z, x) across the two-dimensional (x, z) range [-4, 4] x [-4, 4]. The visualization in a 3D contour diagram results in the following:

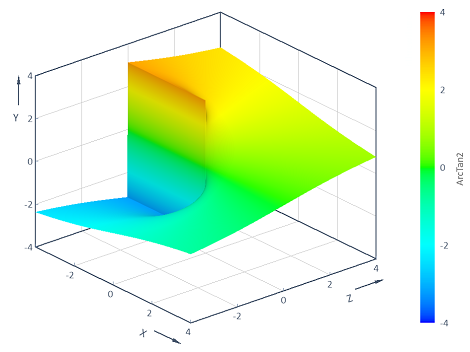
Dim x = Series(-16, 16, 0.04)
Dim z = x
Dim grid = MeshGrid(x, z)
Dim y = Sinc(Sqrt(grid.["X"]^2 + grid.["Z"]^2))
Signal(y, x, z)

Example 3: Visualization of the Sinc function in 2D

Calculates the two-dimensional Sinc function y = f(x, z) = Sinc(Sqrt(x^2 + z^2)) across the two-dimensional (x, z) range [-16, 16] x [-16, 16]. The visualization in a 3D contour diagram results in the following:

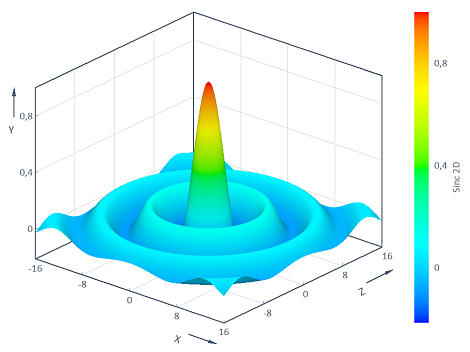
Dim z1 = Series(-6, 6, 0.02)
Dim z2 = z1
Dim grid = MeshGrid(z1, z2)
Dim y = Real(Log(grid.[0] + 1i * grid.[1]))
Signal(y, z1, z2)

Example 4: Visualization of functions with complex arguments

Calculates the real part of the complex logarithm y = f(z1, z2) = Real(Log(z1 + i* z2)) across the complex (z1, z2) plane [-6, 6] x [-6, 6]. The visualization in a 3D contour diagram results in the following:

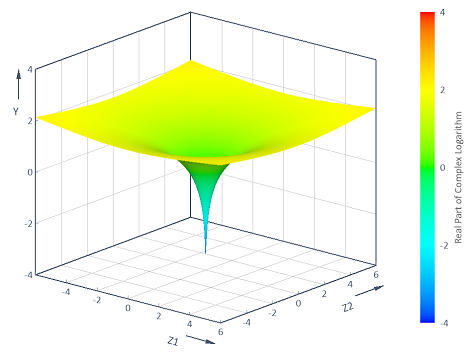
Arguments x, z
Dim xMatrix = x # NumberOfRows(z)
Dim zMatrix = TransposeMatrix(z # NumberOfRows(x))
List("X", xMatrix, "Z", zMatrix)

Example 5: Equivalent FPScript code

The following FPScript code produces the same result as the MeshGrid function.

See Also

ArcTan2 Function

List Function

NumberOfColumns Function

NumberOfRows Function

Reshape Function

Shape Function

TransposeMatrix Function

List Operator

List Element Operator