weisang.com > Dokumentation > Analyseobjekt und -vorlage Nicht-lineare Kurvenanpassung *

FlexPro-Dokumentation

Analyseobjekt und -vorlage Nicht-lineare Kurvenanpassung *

09.03.2021

Mit dem Analyseobjekt Nicht-lineare Kurvenanpassung ist es möglich, eine Modellfunktion in Abhängigkeit von einer unabhängigen Variablen und von mehreren Parametern an einen vorgegebenen Datensatz anzunähern. Dazu stehen eine Reihe vordefinierter Modellfunktionen zur Verfügung. Alternativ lassen sich eigene Modelle definieren.

Iterative und nicht-iterative Verfahren

Bei den Verfahren zur nicht-linearen Kurvenanpassung unterscheidet man zwischen iterativen und nicht-iterativen Verfahren.

Die nicht-iterativen Verfahren sind in der Praxis ungeeignet, da sie sehr zeitintensiv sind. Dies belegt die "Grid-Search"-Methode. Dabei wird der zu durchsuchende Bereich, in dem das Minimum liegt, in ein n-dimensionales (n … Anzahl der Parameter der Funktion) Gitter aufgeteilt. Für jeden Punkt des Gitters werden die Residuen der Funktion berechnet. Der Punkt, bei dem die Residuen-Quadratsumme am geringsten ist, liefert das Ergebnis. Wird nun das Gitter halbiert, so steigt die Anzahl der Funktionsaufrufe um das 2n-fache. Bei der "Random-Search"-Methode sind die zu berechnenden Punkte nicht als Gitter angeordnet, sondern zufallsverteilt. Der Nachteil dieser Methoden liegt darin, dass im Gegensatz zu den iterativen Verfahren die Suche nach den besten Parametern nicht durch vorherige Berechnungen eingegrenzt wird. Somit wird eine Vielzahl "unnötiger" kostspieliger Funktionsaufrufe ausgeführt.

Da bei Verwendung der iterativen Verfahren nicht sichergestellt ist, dass das berechnete Ergebnis ein "globales Minimum" ist, werden mehrfache Berechnungen mit unterschiedlichen Startparametern vorgeschlagen. Dabei sind die nicht-iterativen Algorithmen hilfreich.

In FlexPro steht deshalb die FPScript-Funktion ParameterEstimation zur Verfügung, die sowohl die "Grid-Search"-Methode als auch die "Random-Search"-Methode anbietet. Aufgrund der bereits beschriebenen schlechten Laufzeit eignet sich die Funktion in erster Linie für einfache Modelle mit wenigen Parametern.

Zu den iterativen Verfahren gehören die in der FPScript-Funktion NonLinCurveFit angebotenen Algorithmen, die schrittweise zu einem lokalen Minimum konvergieren.

Dazu werden folgende Schritte durchgeführt:

•Die Startparameter werden für jeden Parameter des ausgewählten Regressionsmodells festgelegt (z. B. mit Hilfe der nicht-iterativen Verfahren)

•Die Kurve wird berechnet, indem die Parameterwerte in die Modellfunktion eingesetzt wird.

•Die Quadratsumme der vertikalen Distanzen zwischen Datenpunkten und Kurve wird berechnet.

•Die Parameter werden so verändert, dass die Kurve sich den Datenpunkten besser annähert. Dazu werden verschiedene Algorithmen benutzt.

•Die Schritte 1 bis 4 werden so lange wiederholt, bis ein "gutes" Ergebnis erzielt wird. Hierfür gibt es diverse Konvergenzkriterien, die festgelegt werden können.

Gesucht werden also die Parameter eines Modells, die die gewichtete Residuen-Quadratsumme möglichst minimieren und somit eine gute Annäherung an einen vorgegebenen Datensatz liefern.

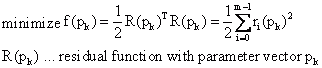
Von einem vorgegebenen Startpunkt aus werden Vektoren mit Parameterwerten berechnet, die gegen ein lokales Minimum konvergieren. Die verschiedenen Methoden unterscheiden sich in der Berechnung der Schrittweite, der Schrittrichtung und den Konvergenzkriterien.

Die angewandten Algorithmen bauen auf folgenden Verfahren auf:

Gauss-Newton-Verfahren

Beim Gauss-Newton-Verfahren wird das Modell mittels Taylorentwicklung linearisiert. Das linearisierte Modell wird dann verwendet, um die Quadratsumme der Residuen zu minimieren.

Methode des steilsten Abstieg (Steepest Descent method)

Bei der Suche nach dem Minimum wird die Richtung des Abstiegs durch den (negativen) Gradienten der Funktion angegeben.

Das Verfahren wird daher auch Gradientenmethode (gradient method) genannt. Sie findet das Optimum in der Regel eher langsam, d. h. sie konvergiert schlecht.

Levenberg-Marquardt-Verfahren

Das Levenberg-Marquardt-Verfahren kombiniert das Gauss-Newton-Verfahren mit der Methode des steilsten Abstiegs. Der in diesem Verfahren verwendete "Trust-Region"-Radius beeinflusst die Schrittweite und Schrittrichtung. Er gibt eine Obergrenze für die euklidische Norm der Suchrichtung vor und beeinflusst somit das verwendete Verfahren (Gauss-Newton oder steilster Abstieg).

Newton-Verfahren

Im Gegensatz zum Gauss-Newton-Verfahren wird der quadratische Teil der Taylorentwicklung betrachtet. Daher wird für die Berechnung die Hesse-Matrix (2. partielle Ableitungen) benötigt. Da die Hesse-Matrix selten analytisch angegeben werden kann, muss sie approximiert werden. Dies geschieht z. B. durch das Sekantenverfahren. Gute Algorithmen zerlegen die Hesse-Matrix, so dass bereits vorhandene Informationen verwendet werden können und somit eine bessere Approximation erzielt wird. Es wird statt H(x) nur S(x) approximiert:

Hessematrix:

Berechnung der nächsten Iteration p+ von einen Punkt pk:

Verfahren	Wird berechnet mit
Gauss-Newton
Levenberg-Marquardt
Newton
NL2SOL

Algorithmen

Bei der nicht-linearen Kurvenanpassung verwendeten Algorithmen handelt es sich um ein Verfahren von Moré im MINPACK Paket (Levenberg-Marquardt-Algorithmus) und eine Variante des NL2SOL-Algorithmus (Full-Newton-Algorithmus). In der Literatur werden beide Algorithmen für etwa gleich gut befunden. Bei Problemen mit kleinen Residuen gibt es keinen großen Unterschied. Der komplexere NL2SOL-Algorithmus ist jedoch bei Problemen mit größeren Residuen bzw. bei stark nicht-linearen Problemen vorzuziehen, da er weniger Iterationen benötigt. Zudem lassen sich in der implementierten Variante des NL2SOL-Algorithmus Grenzen für die zu suchenden Parameter setzen und somit der zu durchsuchende Bereich einschränken. Beide Algorithmen wurden bereits ausführlich auf Anwendbarkeit und Robustheit getestet.

Für beide Algorithmen können die partiellen Ableitungen, die für die Berechnung benötigt werden, sowohl analytisch berechnet werden als auch durch "vorwärts genommene Differenzenquotienten" (forward-difference approximation) approximiert werden. Bei der analytischen Berechnung werden die partiellen Ableitungen als Formeln angegeben. Dies ist bei fast allen vorgegebenen Modellen der Fall. Wird bei einem benutzerdefinierten Modell die Ableitungen nicht angegeben, so werden sie genähert.

Bei dem Algorithmus LMDER bzw. LMDIF in MINPACK handelt es sich um einen modifizierten Levenberg-Marquardt-Algorithmus. Moré verwendet ein skaliertes "Trust-Region" Verfahren.

Der NL2SOL-Algorithmus basiert auf dem Newton-Verfahren für "Least-Squares"-Probleme (Methode der kleinsten Quadrate). Er enthält ein Sekantenverfahren zur Berechnung der Hessematrix. Zudem wird eine "Trust-Region" Strategie verwendet. Für Probleme mit kleinen Residuen vereinfacht sich der Algorithmus zu einem Levenberg-Marquardt- oder einem Gauss-Newton-Verfahren. Beide Algorithmen findet man im Internet unter www.netlib.org.

Modell

FlexPro bietet eine Vielzahl vordefinierter Modell-Funktionen, an die die zu analysierenden Daten angepasst werden können. Nachdem man ein Modell ausgewählt hat, kann man sich die Formel und eine dazugehörige Modellskizze in einem Vorschaufenster ansehen. Über die Schaltfläche Hilfe über Modelle gelangt man direkt zur FlexPro Online-Hilfe der Modellfunktionen. So kann z. B. beim Anpassen der Startwerte der Parameter die aktuelle Modellfunktion betrachtet werden, ohne dass ein Hin- und Herschalten zwischen den Registerkarten erforderlich ist.

Peak-Modelle

Es stehen eine Reihe vordefinierter Peak-Modelle zur Verfügung, die durch die Peak-Anzahl und die Angabe einer Grundlinien-Funktion modifiziert werden können. Bei Modellen mit mehreren Peaks können bestimmte Modellparameter gemeinsam verwendet werden. Dies lässt sich in der Parameter-Liste einstellen. Anhand dieser Angaben wird dynamisch ein "spezielles" Peak-Modell erzeugt und bei der Nicht-linearen Kurvenanpassung verwendet. Das Peak-Fitting bietet FlexPro im Analyseassistenten als separate Analysevorlage an.

Benutzerdefiniertes Modell

Befindet sich das zu analysierende Modell nicht in der Liste der vordefinierten Modellfunktionen, so kann ein benutzerdefiniertes Modell definiert und im Benutzerprofil gespeichert werden. Dazu wählt man im ersten Schritt das Modell (Benutzerdefiniertes Modell) aus. Es erscheint das Eingabefeld Funktion, in das das benutzerdefinierte Modell eingetragen wird. Die Parameter eines benutzerdefinierten Modells mit der Parameteranzahl n haben die Bezeichnungen p[0], p[1], ..., p[n-1]. Die unabhängige Variable ist x.

Beispiel einer Sinus-Funktion: p[0] * sin(2 * PI * p[1] * x + p[2])

Sie können den Parametern auch Namen zuweisen. Diese Namen werden dann in der Liste Startwerte angezeigt. Dazu müssen Sie in der Formel, die die benutzerdefinierte Modellfunktion beschreibt, den Parametervariablen p[0] … p[n-1] Namen zuweisen.

Dim Amplitude = p[0]
Dim Frequenz = p[1]
Dim Phase = p[2]

Die Variable Amplitude wird der Variablen p[0] zugewiesen, die Variable Frequenz der Variablen p[1] und die Variable Phase der Variablen p[2]. Sie müssen darauf achten, dass die Zuweisungen untereinander stehen. In der Modell-Funktion können Sie jetzt die Variablen p[0] bis p[n-1] ersetzen:

Amplitude * sin(2 * PI * Frequenz * x + Phase)

Wichtig bei der Definition eines benutzerdefinierten Modells ist die richtige Eingabe der Parameteranzahl. Ist dieser Wert falsch, so kann die Nicht-lineare Kurvenanpassung nicht berechnet werden oder liefert ein falsches Ergebnis.

•Partielle Ableitungen analytisch berechnen

Die Algorithmen der Nicht-linearen Kurvenanpassung benötigen für die Berechnung die partiellen Ableitungen der Modellparameter. Die Ableitungen können sowohl analytisch berechnet werden als auch durch "vorwärts genommene Differenzenquotienten" (forward-difference approximation) approximiert werden. Bei der analytischen Berechnung werden die partiellen Ableitungen als Formeln angegeben. Die Formel, die die Ableitungen beschreibt, muss als Liste mit n (Anzahl der Parameter) Ableitungsfunktionen angegeben werden.

Beispiel:

Dim Amplitude = p[0]

Dim Frequency = p[1]

Dim Phase = p[2]

[ sin(2 * PI * Frequency * x + Phase), 2 * PI * x * Amplitude * cos(2 * PI * Frequency * x + Phase), Amplitude * cos(2 * PI * Frequency * x + Phase) ]

•Modell speichern

Es gibt die Möglichkeit, ein benutzerdefiniertes Modell im Benutzerprofil zu speichern. Dazu ist es erforderlich, im Listenfeld Modell einen Namen einzutragen und die Schaltfläche Modell speichern zu drücken. Alle gespeicherten Modelle erscheinen im Modell-Listenfeld. Wählt man ein benutzerdefiniertes Modell im Listenfeld aus, so kann es durch Drücken der Schaltfläche Modell löschen aus dem Benutzerprofil gelöscht werden.

•Benutzerdefiniertes Modell aus Formel

Es gibt auch die Möglichkeit, benutzerdefinierte Modelle datenbankabhängig zu speichern, in dem man Formeln mit den Modellfunktionen anlegt. Dazu muss man das Modell (Benutzerdefiniertes Modell aus Formel) wählen und die erzeugte Modell-Formel als Funktion angeben. Die Syntax der Modell-Formeln wird unter Benutzerdefiniertes Modell beschrieben. Allerdings muss der Formelinhalt in Anführungszeichen gesetzt werden, da die Modell-Formeln den Datentyp Zeichenkette haben müssen.

Die Formel für das obige Modell muss z. B. folgendermaßen aussehen:

"Dim Amplitude = p[0]\r\n_
Dim Frequency = p[1]\r\n_
Dim Phase = p[2]\r\n_
Amplitude * sin(2 * PI * Frequency * x + Phase)"

Die Formel für die partiellen Ableitungen muss folgenden Code enthalten:

"Dim Amplitude = p[0]\r\n_
Dim Frequency = p[1]\r\n_
Dim Phase = p[2]\r\n_
[ sin(2 * PI * Frequency * x + Phase),_
2 * PI * x * Amplitude * cos(2 * PI * Frequency * x + Phase),_
Amplitude * cos(2 * PI * Frequency * x + Phase) ]"

Die "\r\n"-Zeichen erzeugen Zeilenwechsel in der Zeichenkette und müssen immer verwendet werden, wenn Ihr Code mehrere Anweisungen enthält. Die "_" wurden hier an den Zeilenenden verwendet, damit die Zeichenkette selbst in mehrere Zeilen umgebrochen werden kann.

Modellbewertung (Nur im Analyseassistent)

Mit diesem Werkzeug können Sie die Berechnung mehrerer Modellfunktionen miteinander vergleichen. Die Bewertung der ausgewählten Modelle erfolgt über die absoluten Quadratsumme der Residuen SSE. Sehen Sie hierzu das Tutorial Nicht-lineare Kurvenanpassung.

Parameter

Entscheidend für das Berechnungsergebnis ist die Wahl der Startwerte der Modellparameter. Liegt der gewählte Startpunkt weit entfernt vom globalen Minimum, so liefert der Algorithmus möglicherweise kein Ergebnis bzw. ein anderes lokales Minimum. Beim Full-Newton-Algorithmus kann für jeden Parameter eine Bereichsgrenze (Ober- und Untergrenze) angegeben werden und somit der Suchbereich eingeschränkt werden.

Es können bestimmte Parameter des ausgewählten Modells als fest deklariert werden. Beim Full-Newton-Algorithmus werden hierzu die Ober- und die Untergrenze auf den angegebenen Startwert gesetzt. Beim Levenberg-Marquardt-Algorithmus wird die Parametervariable in der Modellfunktion durch den konstanten Startwert ersetzt.

Startwerte schätzen (Nur im Analyseassistent)

Um die Wahrscheinlichkeit zu erhöhen, dass es bei dem angezeigten Ergebnis um ein globales Minimum handelt, sollte die Berechnung mit unterschiedlichen Startwerten durchgeführt werden. Für Modelle mit vier oder weniger Parametern steht die Option Startparameter schätzen zur Verfügung. Für jeden Parameter werden jeweils 10 zufallsverteilte Werte berechnet, die sich in dem durch die Untergrenze und Obergrenze festgelegten Bereich befinden. Nun wird für jede Kombination die absolute Quadratsumme der Residuen berechnet. Die Kombination mit der kleinsten Quadratsumme liefert die Startwerte.

Startskript

Die Parameterstartwerte können auch durch eine FPScript-Formel berechnet werden. Dabei muss darauf geachtet werden, dass das Ergebnis der Formel eine Datenreihe mit n (Anzahl der Modellparameter) Werten liefert. Ansonsten wird das Startskript ignoriert. Zur Bearbeitung der Formel klicken Sie auf das Symbol Startskript. In dem Dialogfeld, das dann erscheint, können Sie den Code verändern. Verwenden Sie die Variable data, um auf die Daten zuzugreifen. Mit der Schaltfläche Berechnen zeigen Sie das Ergebnis an. Mit Übernehmen übernehmen Sie die berechneten Parameter. Im Analyseassistenten können Sie zusätzlich die Option Startskript verwenden markieren. Das Startskript wird dann automatisch bei jedem Modellwechsel oder beim erneuten Aufruf der nicht-linearen Kurvenanpassung berechnet.

Gewichtung

Die Ermittlung der besten Parameter mit Hilfe der Minimierung der Quadratsumme der Residuen basiert auf der Annahme, dass die Streuung der Werte um die ermittelte Kurve einer Gauß-Verteilung entspricht. Das Verfahren der kleinsten Fehlerquadrate ist eine Maximum-Likelihood-Schätzung, wenn die Messfehler unabhängig und Normal-verteilt (Gauß-verteilt) sind und eine konstante Standardabweichung haben. Messwerte, die weiter von der angenommenen Kurve entfernt sind, beeinflussen die Quadratsumme der Residuen stärker als nähere Punkte.

Wenn die Streuung bei allen Datenpunkten gleich ist, so ist keine Gewichtung notwendig. Der Gewichtungsvektor W ist für jeden Parameter 1.

Es gibt auch experimentelle Situationen, bei denen der Residuenabstand mit steigendem Y wächst. Falls der absolute Abstand der Punkte zur Kurve mit steigendem Y wächst, der relative Abstand (Abstand geteilt durch Y) aber konstant bleibt, macht eine relative Gewichtung W = 1/Y2 Sinn. Die Quadratsumme der Abstände ist somit:

Die Poisson-Gewichtung W = 1/Y stellt einen Kompromiss zwischen der Minimierung des relativen u. absoluten Abstands dar. Sie ist insbesondere bei einer Poisson-Verteilung sinnvoll:

Darüber hinaus kann die Residuenquadratsumme mit der Varianz gewichtet werden. Werden die zu untersuchenden Daten als Datenmatrix oder Datenreihe angegeben, so wird die Varianz s2 bei der Einstellung "Gewichtung mit 1/s2, 1/s2 wird aus Datenmatrix ermittelt" über die Daten ermittelt und als Gewichtung verwendet:

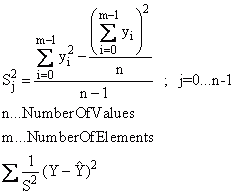
Schließlich lässt sich die Varianz s2 über einen Datensatz anzugeben. Die Datenlänge der Varianz muss der Datenlänge des zu untersuchenden Datensatzes entsprechen.

Skalierung

Ein Problem bei der nicht-linearen Kurvenanpassung kann die schlechte Skalierung der einzelnen Parameter eines Modells sein. Beispielsweise könnte sich eine Variable in einem Bereich [102, 103] Meter und eine andere in einem Intervall [10-7, 10-6] Sekunden bewegen. Ignoriert man diesen Punkt, so kann dies die Berechnungsergebnisse negativ beeinflussen.

Aus diesem Grund stehen für die jeweiligen Algorithmen verschiedene Skalierungsmöglichkeiten (Keine Skalierung, Adaptive Skalierung, Skalierung aus initialer Jakobimatrix, Skalierung anhand der Grenzen, benutzerdefinierte Skalierung) zur Verfügung. Im genannten Beispiel könnte man eine benutzerdefinierte Skalierung wählen und den ersten Parameter in Kilometer und den zweiten Parameter in Millisekunden umrechnen. Beide Parameter liegen dann im Intervall [10-1,1]. Neben dem Einfluss auf den Algorithmus spielt die Skalierung bei der Berechnung diverser Konvergenzkriterien eine wichtige Rolle. Bei der Berechnung ohne Skalierung werden die Parameter mit einem sehr kleinen Wertebereich bei der Prüfung der Konvergenzkriterien vernachlässigt.

Abbruchkriterien und Einstellparameter

Ein wichtiger Punkt bei der Berechnung der Parameter ist das Beenden des Algorithmus. Es stellt sich die Frage, wann eine Berechnung erfolgreich beendet werden kann bzw. wann es Zeit ist, die Berechnung mit einer Fehlermeldung abzubrechen.

Es existieren unterschiedliche Konvergenzkriterien, die beurteilen, ob die aktuell berechneten Parameter der gewünschten Lösung so nahe kommen, dass die Berechnung beendet werden kann. Die Konvergenztoleranzen lassen sich über die Parameter X-Toleranz, Y-Toleranz, F-Toleranz bzw. G-Toleranz einstellen. Die Berechnung der Konvergenzkriterien unterscheidet sich bei den Algorithmen.

•Der Algorithmus NL2SOL enthält 5 Konvergenztests:

- X-Konvergenz (relatives Parameter-Konvergenz-Kriterium) (X-Convergence)

- Relative Funktions-Konvergenz (Relative Function Convergence)

- Absolute Funktions-Konvergenz (Absolute Function Convergence)

- Singuläre Konvergenz (Singular Convergence)

- Falsche Konvergenz (False Convergence)

Die ersten drei Konvergenzkriterien lassen sich über die Einstellmöglichkeiten X-Toleranz, Y-Toleranz und F-Toleranz beeinflussen. Die Absolute Funktions-Konvergenz tritt ein, wenn eine Iteration pk gefunden wird, bei der für eine vorgegebene Toleranz F-Toleranz (FTolerance) gilt:

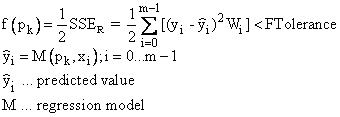
Die anderen Konvergenzkriterien werden nur dann ausgeführt, wenn der aktuelle Schritt Δpk zu nicht mehr als zweimal der vorhergesagten Funktionsreduzierung führt:

Die Konvergenztests beruhen stark auf dem aktuellen quadratischen Modell qk, welches ziemlich unzuverlässig ist, wenn die angegebene Ungleichung nicht erfüllt ist. Diese Prüfung bietet somit einen zusätzlichen Schutz in Bezug auf die Zuverlässigkeit der anderen Konvergenzkriterien.

Die X-Konvergenz (XTolerance) prüft die relative skalierte Änderung der Parameter pro Iterationsschritt:

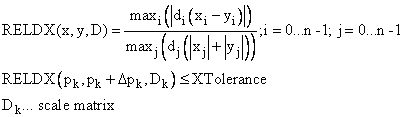
Die Relative Funktionskonvergenz (YTolerance) wird erreicht, wenn die Funktion mit den aktuell berechneten Parametern nahe an einer geschätzten Funktion f(p*) mit einem starken lokalen Minimierer p*. liegt Die geschätzte Funktion wird durch ein quadratisches Modell genähert:

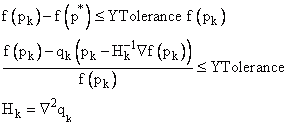
•Minpack:

Die relative Parameterkonvergenz (X-Konvergenz) basiert auf dem Verhältnis zwischen der absoluten Änderung der Parameter zu der relativen Änderung der euklidischen Norm der Parameter. Dieses Konvergenzkriterium lässt sich durch den X-Toleranz-Parameter beeinflussen.

Zur Prüfung der relativen Funktionskonvergenz berechnet der MINPACK-Algorithmus LMDER bzw. LMDIF die aktuelle relative Änderung bei der Summe der Quadrate während einer Iteration und die geschätzte relative Änderung basierend auf einem linearen Modell. Das Konvergenzkriterium ist erfüllt, wenn beide relativen Änderungen kleiner als die vorgegebene Toleranz Y-Toleranz sind.

Mit dem Parameter G-Toleranz legt man fest, wie groß der Kosinus des Winkels zwischen den Spalten der aktuellen Jakobimatrix und dem entsprechenden Residuenvektor sein darf. Es lässt sich somit die Orthogonalität festlegen. Es lässt sich ein mathematischer Zusammenhang zwischen diesem Test und dem Test zur Prüfung der relativen Parameterkonvergenz im Algorithmus NL2SOL herstellen (vgl. Dennis: An Adaptive Non-Linear Least Square Algorithm).

Zusätzlich lässt sich angeben, wie oft die Funktion zur Berechnung der Residuen maximal aufgerufen werden darf, bevor die Berechnung abgebrochen wird. Es kann vorkommen, dass pro Iterationsschritt mehrmals die Residuenfunktion aufgerufen wird. Daher lässt sich nicht die maximale Iterationsanzahl sondern die maximale Anzahl der Funktionsaufrufe angeben.

Mit der Schrittgrenze lässt sich die Anfangsschrittweite verändern. Diese muss unter Umständen verändert werden, um einen zu großen ersten Schritt zu verhindern, der zum Beispiel zu einem Überlauf des Exponenten führt. Es wird der Durchmesser der "Trust-Region", in dem nach den besten Parametern bei der ersten Iteration gesucht werden darf, festgelegt.

Ergebnis / Ausgabe (Nur im Analyseobjekt)

Die Statusausgabe beschreibt den Grund für den Abbruch einer Berechnung. Es wird zwischen zwei Gruppen unterschieden. Der Algorithmus wird erfolgreich beendet, wenn bestimmte Konvergenzkriterien erfüllt sind. Ist dies nicht der Fall, so bricht der Algorithmus aufgrund von Abbruchkriterien die Berechnung ab. Die Konvergenzkriterien allein reichen jedoch nicht aus, um das Ergebnis der Nicht-linearen Kurvenanpassung zu beurteilen. Daher stehen verschiedene statistische Ausgabeoptionen zur Verfügung, mit deren Hilfe die Güte der Anpassung beurteilt werden kann.

Die Nicht-lineare Kurvenanpassung bietet Ihnen zwei Ausgabealternativen. Sie können die Parameter einmalig berechnen und statisch in die gewählte Modellfunktion eintragen. Dazu existiert die Funktion NonLinModel für die vordefinierten Modelle. Um ein statisches Modell zu erzeugen, müssen Sie die Schaltfläche Kurvenanpassung berechnen drücken. Die berechneten Werte werden in der Parameter-Liste angezeigt. Alternativ können Sie in der Registerkarte Ausgabe festlegen, welche statistischen Kenngrößen ausgegeben werden sollen. Wenn mehrere Ausgabeoptionen ausgewählt werden, so liefert das Analyseobjekt als Ergebnis eine Liste. (Siehe NonLinCurveFit)

Literatur

•P.R. Bevington, D.K. Robinson. Data Reduction and Error Analysis for the Physical Sciences, 3nd Ed., McGraw-Hill, New York, 2003.

•W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery. Numerical Recipes in C. 2nd ed. Cambridge, U.K., Cambridge Univ. Press, 1992.

•G. A. F. Seber, C. J. Wild. Nonlinear Regression. Wiley, New York, 2003.

•K. Madsen, H.B. Nielsen, O. Tingleff, Methods for non-linear least squares problems, 2nd Edition, IMM, DTU, April 2004, Internet: http://www.imm.dtu.dk/courses/02611/nllsq.pdf

•P.E. Frandsen, K. Jonasson, H. B.Nielsen. Unconstrained Optimization, 3nd Edition, IMM, DTU, March 2004, Internet: http://www.imm.dtu.dk/courses/02611/uncon.pdf

•Harvey Motulsky, Arthur Christopoulos. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. Oxford University Press, 2004.

Informationen über die Algorithmen finden Sie in:

•J. E. Dennis Jr., Robert B. Schnabel. Numerical Methods for Unconstrained Optimization and Nonlinear Equations. Classics in Applied Mathematics 16, SIAM Society for Industrial and Applied Mathematics, 1996.

•J. E. Dennis, Jr., D. M. Gay, and R. E. Welsch. An Adaptive Nonlinear Least Square Algorithm, ACM Trans. Math. Software 7, 1981, pp. 348-368 and 369-383

•J. E. Dennis, Jr., D. M. Gay, and R. E. Welsch. Algorithm 573. NL2SOL -- An adaptive nonlinear least-squares algorithm, ACM Trans. Math. Software 7, 1981, pp. 369-383.

•D.W. Marquardt. An Algorithm for Least-Squares Estimation of Nonlinear Parameters, Journal of the Society for Industrial and Applied Mathematics, vol. 11, 1963, pp 431-441.

•Jorge J. Moré. The Levenberg-Marquardt Algorithm: Implementation and Theory, Numerical Analysis, Lecture Notes in Mathematics, vol. 630, G.A. Watson, ed. (Berlin: Springer Verlag), 1977, pp. 105- 116.

•J. J. Moré, B. S. Garbow, and K. E. Hillstrom. User Guide for MINPACK-1, Argonne National Laboratory Report ANL-80-74, Argonne, Ill., 1980. Internet: http://www.netlib.org/minpack/ex/file06

•P. A. Fox, A. D. Hall, and N. L. Schryer. The PORT mathematical subroutine library, ACM Trans. Math. Software 4, 1978, pp. 104-126.

•D. M. Gay. Usage summary for selected optimization routines, Computing Science Technical Report No. 153, AT\&T Bell Laboratories, Murray Hill, NJ, 1990.

•K.L. Hierbert. An Evaluation of Mathematical Software that Solves Nonlinear Least Squares Problems. ACM Trans. Math. Software, Vol 7, No. 1, 1981, pp. 1-16.