Analyseobjekt Rosettentransformation *
Mit diesem Analyseobjekt können Sie aus zwei bzw. drei mit Hilfe einer DMS-Rosette gemessenen Dehnungssignalen verschiedene Größen wie z.B. die Hauptspannungen oder Hauptdehnungen berechnen.
Eine DMS-Rosette ist eine Anordnung von zwei oder mehr nahe beieinanderliegender DMS-Gitter unterschiedlicher Ausrichtung zur Messung der Normaldehnungen auf der sich darunter befindlichen Oberfläche eines Messobjekts. Für den Fall eines zweiachsigen Spannungszustands, dessen Hauptrichtungen unbekannt sind, genügen drei voneinander unabhängige Dehnungsmessungen in verschiedenen Richtungen, um die Hauptdehnungen und Hauptspannungen zu bestimmen.
Rosetteneigenschaften
Die Berechnung ist für folgende Rosettentypen möglich:
Bezeichnung |
Beschreibung |
|---|---|
T-Rosette |
Zwei senkrecht zueinanderstehende Gitter; Position a und b |
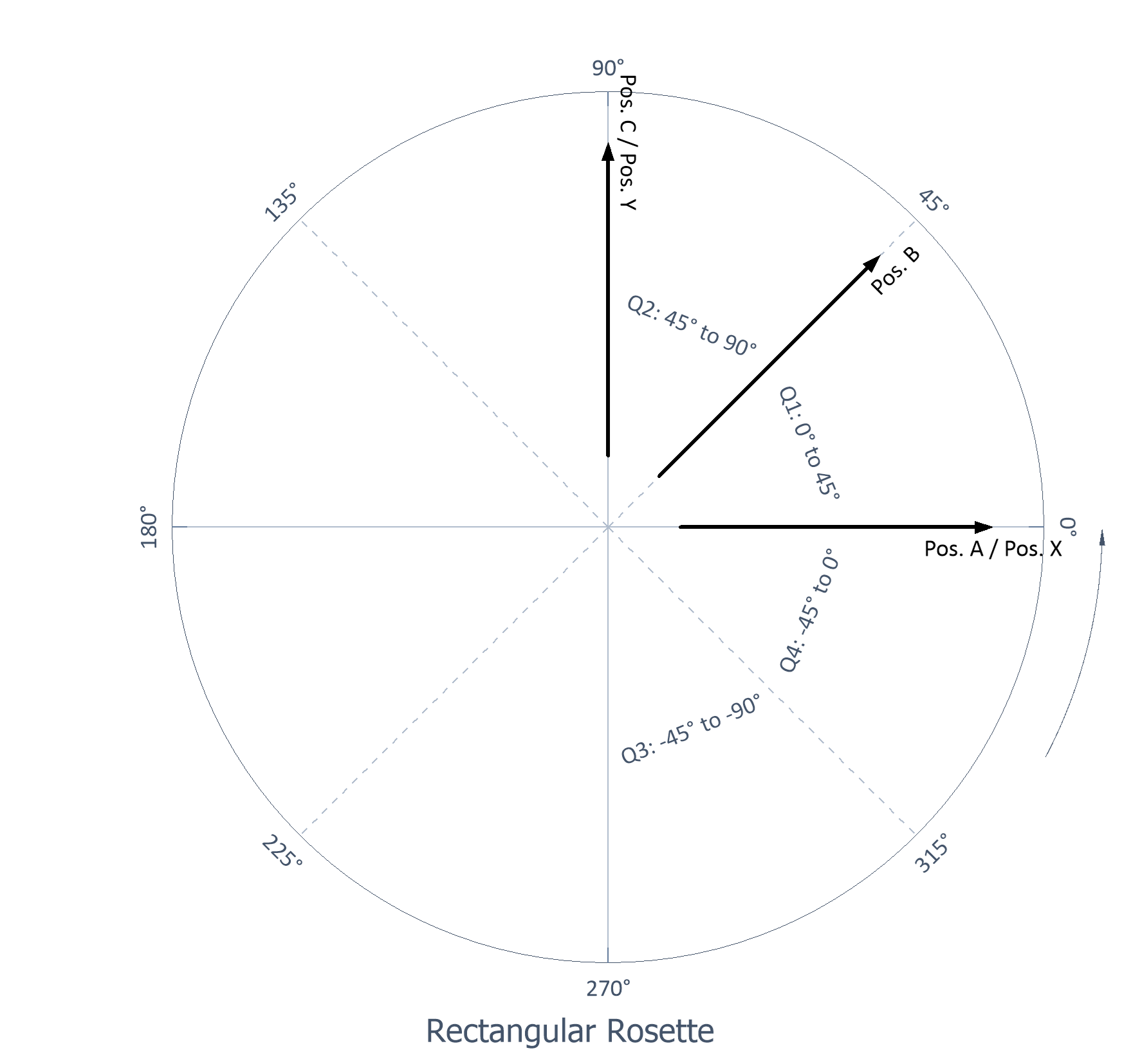
Rechtwinkel-Rosette |
Drei Gitter mit 45° Abstand |
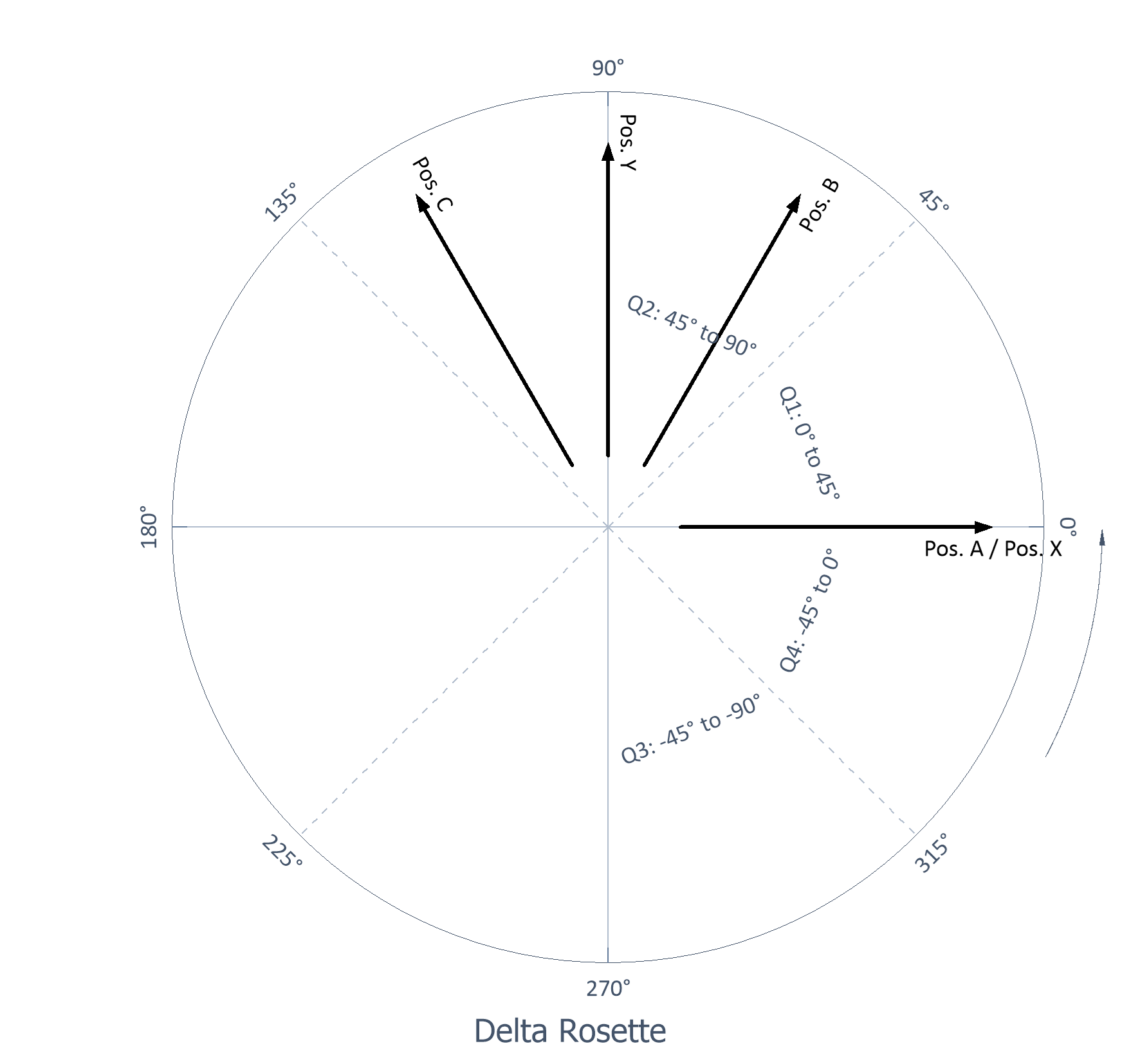
Delta-Rosette |
Drei Gitter mit 60° bzw. 120° Abstand |
Ist der Werkstoff des Messobjekts in seiner Zusammensetzung homogen, verhält er sich isotrop und zeigt er ein lineares Spannungs-/Dehnungsverhältnis, dann kann das Hook'sche Gesetz für den zweiachsigen Spannungszustand angewandt werden, um aus den Hauptdehnungen die Hauptspannungen zu berechnen. Hierfür ist die Kenntnis des Elastizitätsmoduls E (Youngscher Modul) und der Querkontraktionszahl des zu messenden Werkstoffs erforderlich [1, 2].
Querempfindlichkeit
Der Begriff Querempfindlichkeit oder Querdehnungsempfindlichkeit bezieht sich auf die Reaktion von Dehnungsmessstreifen (DMS), wenn Dehnungen quer zur Gitterlängsachse auf sie einwirken. Idealerweise ist es wünschenswert, dass DMS gegen solche Querdehnungen total unempfindlich sind. In der Praxis sind jedoch die meisten DMS zu einem gewissen Grade querdehnungsempfindlich. Glücklicherweise ist die Querempfindlichkeit moderner Folien-DMS sehr klein und bewegt sich in der Größenordnung von einigen Prozent der Dehnungsempfindlichkeit in Gitterrichtung. Die Größe der Querdehnungsempfindlichkeit ist abhängig von der Gitterlegierung und der Gittergeometrie.
Durch Angabe der Querempfindlichkeit kann eine mathematische Korrektur vorgenommen werden [3]. Mit dem Analyseobjekt können die korrigierten Dehnungssignale ausgegeben werden und so mit den gemessenen Dehnungssignalen verglichen werden.
Temperaturkompensation
Optional kann eine Temperaturkompensation für die gemessenen Dehnungssignale durchgeführt werden. Hier wird vorausgesetzt, dass es sich um selbst kompensierende Dehnungsmessstreifen handelt, d.h. der Einfluss des Kabelwiderstands ist bereits eliminiert. Der Temperatureinfluss der DMS-Anschlussbändchens wird ebenfalls nicht berücksichtigt. Die Ermittlung des Restfehlers erfolgt durch eine im Datenblatt des Dehnungsmessstreifens angegebene Polynomialfunktion. Neben der Polynomialfunktion enthält die verwendete Formel Terme für die Temperaturabhängigkeit des k-Faktors und die Abweichung zwischen dem thermischen Ausdehnungskoeffizienten des Werkstoffmaterials, an dem die Messung durchgeführt wurde, und dem thermischen Ausdehnungskoeffizienten des DMS-Gitterwerkstoffs [4, 5].
Die Polynomialkoeffizienten werden als Datenreihe angegeben. Der erste Wert entspricht dem Koeffizienten a0, der zweite Wert dem Koeffizienten a1, usw..
Für die Temperaturkompensation wird folgende Formel verwendet:
Bezeichnung |
Symbol |
|
|---|---|---|
Dehnungsdatensatz |
εu(T) |
|
Temperaturdatensatz |
T |
|
Polynomialkoeffizienten |
a0, a1, a2, ... |
|
Referenztemperatur |
TRef |
|
k-Faktor |
kD |
|
Material-Ausdehnungskoeffizient |
αM |
|
Temperaturkoeffizient des k-Faktors |
αk |
|
DMS-Ausdehnungskoeffizient |
αSG |
Ausgabeoptionen
Folgende Ausgabeoptionen sind verfügbar:
Bezeichnung |
Beschreibung |
|
|---|---|---|
Hauptdehnung 1 |
Hauptdehnung 1 |
|
Hauptdehnung 2 |
Hauptdehnung 2 |
|
Hauptspannung 1 |
Spannung in Richtung der Hauptdehnung 1 |
|
Hauptspannung 2 |
Spannung in Richtung der Hauptdehnung 2 |
|
Winkel |
Winkel |
|
Schubdehnung |
Schubdehnung |
|
Schubspannung |
Spannung in Richtung der Schubdehnung |
|
Vergleichsspannung nach von Mises |
Vergleichsspannung nach von Mises |
|
Dehnung X |
Entspricht der korrigierten Dehnung an Position a |
|
Dehnung Y |
Entspricht der um 90° gegen den Uhrzeigersinn verschobenen Dehnung von Position a |
|
Spannung X |
Spannung in Richtung der Dehnung X |
|
Spannung Y |
Spannung in Richtung der Dehnung Y |
|
Korrigierte Dehnung an Position a |
Mit Hilfe der Querempfindlichkeit korrigierte Dehnung an Position a |
|
Korrigierte Dehnung an Position b |
Mit Hilfe der Querempfindlichkeit korrigierte Dehnung an Position b |
|
Korrigierte Dehnung an Position c |
Mit Hilfe der Querempfindlichkeit korrigierte Dehnung an Position c |
Berechnungsformeln
T-Rosette:
Bezeichnung |
Formel |
|
|---|---|---|
Hauptdehnung 1 |
||
Hauptdehnung 2 |
||
Hauptspannung 1 |
||
Hauptspannung 2 |
||
Winkel |
90° |
|
Schubdehnung |
0 |
|
Schubspannung |
||
Vergleichsspannung nach von Mises |
||
Dehnung X |
entspricht Hauptdehnung 1 |
|
Dehnung Y |
entspricht Hauptdehnung 2 |
|
Spannung X |
entspricht Hauptspannung 1 |
|
Spannung Y |
entspricht Hauptspannung 2 |
|
Korrigierte Dehnung an Position a, Position b |
Rechtwinkel-Rosette:
Bezeichnung |
Formel |
|
|---|---|---|
Hauptdehnung 1 |
||
Hauptdehnung 2 |
||
Hauptspannung 1 |
||
Hauptspannung 2 |
||
Winkel |
||
Schubdehnung |
||
Schubspannung |
||
Vergleichsspannung nach von Mises |
||
Dehnung X |
||
Dehnung Y |
||
Spannung X |
||
Spannung Y |
||
Korrigierte Dehnung an Position a, Position b |
Delta-Rosette:
Bezeichnung |
Formel |
|
|---|---|---|
Hauptdehnung 1 |
||
Hauptdehnung 2 |
||
Hauptspannung 1 |
||
Hauptspannung 2 |
||
Winkel |
||
Schubdehnung |
||
Schubspannung |
||
Vergleichsspannung nach von Mises |
||
Dehnung X |
||
Dehnung Y |
||
Spannung X |
||
Spannung Y |
||
Korrigierte Dehnung an Position a, Position b |
mit
Literatur
[1] Micro-Measurements. Tech Note TN-515: Strain Gage Rosettes: Selection, Application and Data Reduction. Document Number: 11065, Revision 14-Aug-2014.
[2] Karl Hoffmann. An Introduction to Stress Analysis using Strain Gauges. www.hbm.com
[3] Micro-Measurements. Tech Note TN-509: Errors Due to Transverse Sensitivity in Strain Gages. Document Number: 11059, Revision 28-Jun-2011.
[4] Hottinger Baldwin Messtechnik GmbH. Technical Information T05414_01_E00_01: Temperature compensation of strain gauge ¼-bridges – Clear, brief and understandable
[5] Micro-Measurements. Tech Note TN-504-1: Strain Gage Thermal Output and Gage Factor Variation with Temperature. Document Number: 11054, Revision 14-Aug-2014.
Verwendete FPScript-Funktionen
StrainGaugeTemperatureCompensation
* Dieses Analyseobjekt ist in FlexPro View und FlexPro Basic nicht verfügbar.
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen