ACF (FPScript)
Berechnet die Autokorrelationsfunktion eines Signals. Beschreibt die Ähnlichkeit eines Signals mit sich selbst.
Syntax
ACF(Signal [ , Mode = CORRELATIONPRODUCT_NONCIRCULAR ])
Die Syntax der ACF-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Signal |
Der Datensatz, dessen Autokorrelationsfunktion berechnet wird. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal und Signalreihe. Es sind alle numerischen Datentypen erlaubt. Ungültige Werte sind in diesem Argument nicht zulässig. Für die X-Komponente gelten zusätzliche Beschränkungen.Die Werte müssen einen konstanten positiven Abstand haben. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||||||||
Mode |
Gibt den Berechnungsmodus an. Das Argument Mode kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert CORRELATIONPRODUCT_NONCIRCULAR gesetzt. |
Anmerkungen
Der Datentyp des Ergebnisses ist immer 64-Bit Fließkomma.
Die Struktur des Ergebnisses entspricht der des Arguments Signal.
Die Einheit des Ergebnisses ist gleich dem Quadrat der Einheit von Signal. Die Autokorrelation für eine Datenreihe s ist definiert als:
![]()
mit dem Korrelationsprodukt:
![]()
und N, der Anzahl der Werte in s.
Die Werte der normierten Autokorrelation liegen zwischen -1 und +1. Die normierte Autokorrelation berechnet sich hierbei als Quotient zwischen Autokorrelation und dem Produkt der RMS-Werte der Eingangsdatensätze.
Die Berechnung erfolgt in allen Fällen im Frequenzbereich nach folgender Formel:
IRFFTn(*FFTn(Signal) * FFTn(Signal))
Bei zweidimensionalen Argumenten erfolgt die Berechnung spaltenweise und das Ergebnis ist ebenfalls zweidimensional. Hat der Eingangsdatensatz eine X-Komponente, so gilt dies auch für das Ergebnis.
Bei der zirkulären Autokorrelation erfolgt die Berechnung unter der Annahme, dass im Datensatz eine oder mehrere vollständige Perioden des Signals abgelegt sind. Falls das Ergebnis eine X-Komponente hat, dann enthält diese den Zeitversatz τ der Autokorrelationsfunktion. Der Wert τ = 0 befindet sich immer am Anfang der X-Datenreihe. Es werden also keine negativen τ berechnet. Wegen der Periodizität der Autokorrelation können in diesem Fall die Werte in der zweiten Hälfte des Ergebnisses jedoch auch als negative τ aufgefasst werden.
Die nicht-zirkuläre Autokorrelation basiert auf der Annahme, dass das Signal außerhalb des durch den Datensatz Signal abgedeckten Ausschnittes den Betrag Null hat. Vor dem Übergang in den Frequenzbereich wird deshalb eine ausreichende Anzahl von Nullen an den Datensatz angehängt. Die Autokorrelationsfunktion wird für alle τ berechnet, für die diese einen Wert ungleich 0 haben kann, d. h. für die noch eine Überlappung des Signals mit seiner verschobenen Kopie vorliegt. Falls das Ergebnis eine X-Komponente hat, dann enthält diese den Zeitversatz τ der Autokorrelationsfunktion. Der Wert τ = 0 befindet sich immer genau in der Mitte der X-Datenreihe.
Folgende Grafik zeigt die verschiedenen Varianten für ein Sinussignal mit Frequenz 1, Amplitude 10 und einem X-Bereich von 0 bis 10:
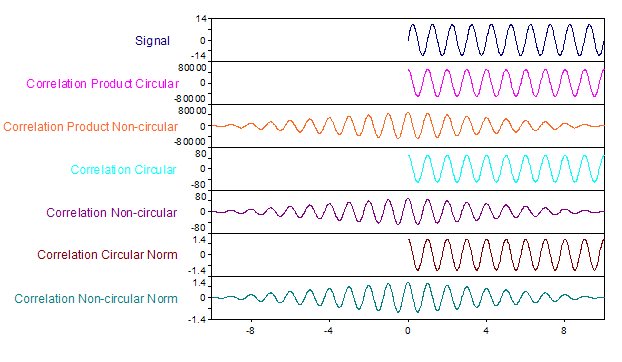
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
ACF(Signal(2. * Sin(2. * PI * 200. * (1000, 0., 1.e-005)) + Noise((1000, 0., 1.e-005), NOISE_NORMAL), (1000, 0., 1.e-005)), CORRELATION_CIRCULAR)
Es liegt ein Sinussignal mit einer Frequenz f = 200 Hz, einer Amplitude = 2 V, Phase = 0° und einem Gleichanteil = 0 V über zwei Perioden vor. Das Signal ist mit einem Gauß-Rauschen (Mittelwert μ = 0 V, Standardabweichung σ = 1 V) überlagert.
Mithilfe der Autokorrelationsfunktion ACF wird nun die Amplitude und die Frequenz des gestörten periodischen Signals zurückgewonnen.
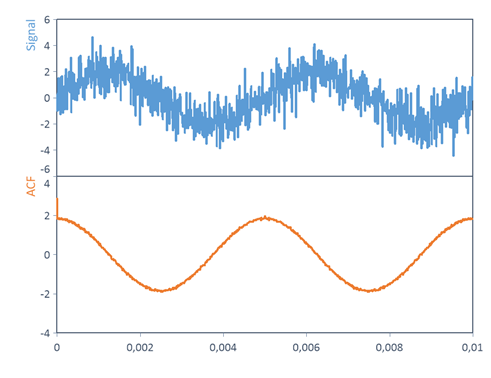
Siehe auch
Literatur
[1] "Oppenheim, A. V. and Schafer, R. W.": "Discrete-Time Signal Processing, 2nd Edition", Seite 743 - 48. "Prentice Hall, New Jersey",1999.ISBN 0-13-754920-2.
[2] "H.D. Lüke": "Signalübertragung", Seite 79 - 81. "Springer-Verlag Berlin, Heidelberg, New York",1985.ISBN 3-540-15526-0.
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen