Correlation (FPScript)
Ermittelt die Korrelationsmatrix einer Datenmatrix bzw. die Korrelation zweier Datensätze.
Syntax
Correlation(DataSet)
oder
Correlation(DataSet1, DataSet2 [ , Mode = PROCESS_COLUMNS ])
Die Syntax der Correlation-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||
|---|---|---|---|---|---|---|---|
DataSet |
Eine Datenmatrix oder Signalreihe, deren Korrelationsmatrix berechnet werden soll. Erlaubte Datenstrukturen sind Datenmatrix, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||
DataSet1 |
Der erste auszuwertende Datensatz. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||
DataSet2 |
Der zweite auszuwertende Datensatz. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||
Mode |
Gibt an, wie zwei Datenmatrizen bzw. Signalreihen verarbeitet werden sollen. Das Argument Mode kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert PROCESS_COLUMNS gesetzt. |
Anmerkungen
Das Ergebnis ist immer vom Datentyp 64-Bit Fließkomma.
Die Korrelation zweier Stichproben ist definiert als:
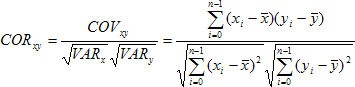
mit den Mittelwerten
![]()
und
![]()
Der Wertebereich der Funktion ist das Intervall [-1, 1].
Wird die Funktion mit einem Argument verwendet, dann muss dies eine Datenmatrix oder eine Signalreihe sein. Die Funktion berechnet dann die Korrelationsmatrix für die Spalten in DataSet.
Wenn Sie DataSet1 und DataSet2 angeben, dann sind beliebige Kombinationen der Datenstrukturen Datenreihe, Datenmatrix, Signal und Signalreihe erlaubt. Bei zusammengesetzten Datenstrukturen wird nur die Y-Komponente verrechnet und die X- oder Z-Komponente wird, sofern möglich, in das Ergebnis übernommen. Diese wird bevorzugt aus DataSet1 entnommen.
Ist die Y-Komponente beider Datensätze eindimensional, dann ist das Ergebnis ein Einzelwert mit der Korrelation beider Datensätze. Ist die Y-Komponente eines Datensatzes eindimensional und die des anderen zweidimensional, dann wird für jede Spalte des zweidimensionalen Datensatzes die Korrelation mit dem jeweils anderen Datensatz berechnet. Das Ergebnis ist eine Datenreihe bzw. ein Signal mit einer Korrelation pro Spalte.
Sind die Y-Komponenten beider Datensätze zweidimensional, dann wird, je nach Einstellung von Mode, für jede Spalte oder Zeile in DataSet1 die Korrelation mit der entsprechenden Spalte bzw. Zeile in DataSet2 berechnet. Das Ergebnis ist eine Datenreihe bzw. ein Signal mit einer Korrelation pro Spalte oder Zeile.
Weisen die Datensätze unterschiedliche Zeilen- oder Spaltenanzahlen auf, dann werden die jeweils überschüssigen Zeilen oder Spalten ignoriert.
Verfügbarkeit
Option Erweiterte Statistik
Beispiele
Correlation({5, 3, 4}, {3, 2, 1}) |
Ergibt 0.5. |
Correlation({{1, 3, 5, 2, 4}, {2, 6, 10, 4, 8}}) |
Ergibt {{2.5, 1}, {1, 10}}. |
Correlation({{1, 3, 5}, {3, 2, 4}}, {{2, 3, 7}, {3, 4, 6}}, PROCESS_ROWS) |
Ergibt {1, -1, 1}. |
Siehe auch
Literatur
[1] "Hartung, Joachim": "Statistik, 9. Auflage", Seite 119 - 20. "Oldenbourg Verlag GmbH, München",1993.ISBN 3-486-22055-1.
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen