L'ajustement de courbe non linéaire permet de faire converger une fonction modèle dépendant d'une variable indépendante et de plusieurs paramètres vers un ensemble de données donné. Cet objet d'analyse est principalement utilisé pour déterminer les paramètres du modèle afin que le modèle sélectionné soit adapté aux données de la meilleure façon possible. Il est ici essentiel d'avoir une connaissance précise du modèle sélectionné et de ses paramètres. L'ajustement non linéaire de la courbe peut toutefois être utilisé pour interpoler ou lisser un ensemble de données donné. Dans ce cas, il n'est pas essentiel de savoir quel modèle doit être utilisé pour l'analyse. De même, le test du paramètre calculé du modèle a lieu. Pour ce domaine d'application, un outil permettant de comparer les modèles disponibles entre eux (évaluation des modèles) est utile.

Exemple :

Un morceau d'argent est irradié pour générer deux isotopes d'argent à courte durée de vie, 47Ag108 et 47Ag110, qui subissent ensuite un nouveau rayonnement bêta. Pour l'expérience, les particules bêta rayonnées sont comptées à intervalles de 15s pendant une période de 4 minutes. Le résultat est une courbe exponentielle décroissante qui est décrite par la fonction modèle Fonction de décroissance exponentielle (variante 2). Le paramètre p0 correspond au rayonnement de fond et p1 et p3 correspondent aux amplitudes des deux états excités avec les vies moyennes p2 et p4 respectivement. Comme le modèle est non linéaire pour les paramètres p2 et p4, une méthode d'ajustement de la courbe non linéaire est nécessaire.

Sélectionnez la commande Fichier > Ouvrir Base de données projet et ouvrez la base de données projet C:\Users\Public\Documents\Weisang\FlexPro\2021\Exemples\CurveFitting.fpd ou C:>Utilisateurs>Public>Documents publics>Weisang>FlexPro>2021>Examples>Tutorials>Curve Fitting.fpd. Ouvrez le dossier appelé Exemple Argent, puis double-cliquez pour ouvrir le graphique 2D appelé Graphique Ag.

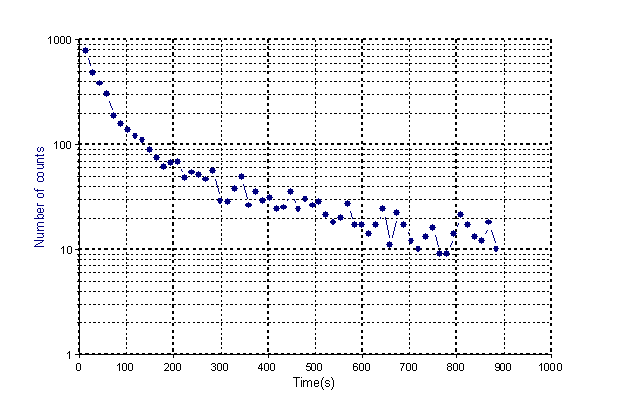
Ceci est le graphique pour le signal Ag avec 59 valeurs à virgule flottante. (Source : Bevington, p. 142 ff)

Évaluation des modèles

Fermez le graphique et sélectionnez l'ensemble de données Ag, le signal à analyser pour l'expérience décrite ci-dessus.

Cliquez sur Insérer[Analyses] > Assistant d'analyse.

Sélectionnez la catégorie Ajustement de courbes, puis Ajustement de courbes non linéaires. Cliquez sur Suivant. Cliquez sur Évaluation modèles... pour déterminer le modèle qui s'applique le mieux à l'ensemble de données sélectionné.

Une boîte de dialogue s'ouvre où vous pouvez choisir l'algorithme, le nombre maximum d'appels de fonction et les catégories de modèles. Vous trouverez l'affectation des différentes fonctions des modèles sous Modèles. Pour l'algorithme , sélectionnez Full Newton. Définissez le nombre maximum d'appels de fonction à 300 et mettez en surbrillance toutes les catégories. Plus la valeur que vous sélectionnez pour les appels maximums de fonction est élevée, plus le nombre de modèles renvoyés en résultat sera important. Le temps nécessaire au calcul de l'algorithme augmentera toutefois en conséquence. Cliquez sur Suivant.

Un ajustement de courbe non linéaire sera ensuite effectué pour tous les modèles sélectionnés et les modèles basés sur la somme des carrés résiduels absolus SSE seront triés et répertoriés. Vous pouvez choisir dans la liste le modèle que vous souhaitez continuer à utiliser. Le coefficient de détermination multiple R2 sera également indiqué. R2 = 1,0 signifie que la courbe passe par chaque point de données. Avec une valeur X connue, la valeur Y associée est déterminée avec précision. R2 = 0,0 signifie que le modèle de régression ne décrit pas mieux les données que sous la forme d'une ligne horizontale passant par la valeur moyenne des données. Les valeurs X connues ne sont d'aucune aide pour calculer la valeur Y associée.

Sélectionnez le modèle dont la somme des carrés absolus des résidus est la plus petite, le modèle NIST modèle de Hahn1, pour obtenir la convergence la plus proche possible. Fermez maintenant la boîte de dialogue Évaluation des modèles en cliquant sur Terminer. Cliquez sur Suivant deux fois. Activez l'option Graphiques et tableaux présentant les résultats. Ensuite, cliquez sur Terminer.

Ouvrez le graphique Signal nouvellement créé pour visualiser le résultat du lissage du signal. Le graphique suivant montre le résultat en échelle logarithmique.

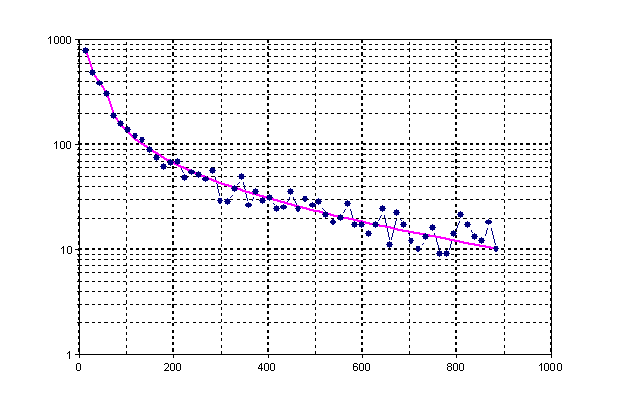
Approximation linéaire

Avant de déterminer les paramètres du modèle à l'aide de l'ajustement non linéaire de la courbe, le signal à analyser est réduit et transformé de manière à pouvoir utiliser une approximation linéaire pour déterminer les paramètres du modèle. Cette méthode peut être utilisée pour calculer les paramètres initiaux. Dans de nombreux cas, la sélection des paramètres initiaux est un critère décisif pour le calcul réussi des paramètres du modèle à l'aide de l'ajustement non linéaire des courbes. Le résultat de la linéarisation dans ce cas sert de contrôle de validation du résultat de l'ajustement de la courbe non linéaire.

La fonction modèle à examiner, Fonction de décroissance exponentielle (variante 2), a le format suivant :

Tout d'abord, le rayonnement de fond (paramètre p0) est déterminé. Un coup d'œil à la courbe du signal suffit pour une estimation approximative. La courbe exponentielle correspond approximativement au décalage à déterminer. Pour obtenir une estimation approximative du rayonnement de fond, on fait la moyenne des trois dernières valeurs du signal. On obtient ainsi la valeur 13,3. Pour déterminer des paramètres supplémentaires, le décalage est soustrait de chaque point du signal. Le signal calculé est réduit à deux segments partiels A (x < 120) et B (x > 200). Les paramètres p3 et p4 sont maintenant approximés par une transformation logarithmique et une approximation linéaire.

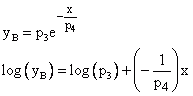
Sur la base de ce résultat, le composant à long terme peut être déterminé. Cette partie est ensuite soustraite du segment A pour déterminer le composant à court terme . Ici, une transformation logarithmique et une approximation linéaire interviennent également.

Les paramètres déterminés sont les suivants :

Ouvrez la formule Linéarisation du dossier Exemple Argent pour voir la fonction FPScript de ce calcul.

Estimation des paramètres

Après cette estimation approximative des paramètres, vous pouvez commencer à déterminer les paramètres précis du modèle.

Pour ce faire, sélectionnez le signal Ag.

Cliquez sur Insérer[Analyses] > Assistant d'analyse.

Sélectionnez la catégorie Ajustement de courbes, puis Ajustement de courbes non linéaires. Cliquez sur Suivant. Sélectionnez le modèle Fonction de décroissance exponentielle (variante 2). En outre, vous pouvez afficher une bande de prédiction (95%, 99% ou 99,9%) et une bande de confiance (95%, 99% ou 99,9%). La bande de confiance est utile pour les données répétitives, c'est-à-dire que pour chaque valeur X, il existe plusieurs valeurs Y ou une valeur Y qui représente la moyenne de plusieurs points mesurés. Un intervalle de confiance à 95% est l'intervalle Y pour une valeur X donnée qui contient la vraie valeur Y avec une probabilité de 95%. La bande de prédiction fait une déclaration sur la dispersion des données à analyser. Si vous collectiez davantage de points de données, 95 % des points se situeraient dans la fourchette de la bande de prédiction.

Après avoir sélectionné le modèle, vous pouvez observer directement le résultat de l'ajustement de la courbe non linéaire dans le volet Aperçu de l'assistant. Dans le premier graphique, le signal d'entrée et le signal estimé sont affichés. Dans un autre graphique, les résidus sont affichés. Dans les deux tableaux, vous trouverez les paramètres estimés et un certain nombre de valeurs statistiques pour le résultat de l'analyse. Les paramètres du modèle calculés ont les valeurs :

Dans ce cas, p1 et p2 sont les paramètres des composants à longue durée de vie, et p3 et p4 sont les paramètres des composants à courte durée de vie.

Cliquez sur Suivant. Sur cette page de l'assistant, divers paramètres sont disponibles qui peuvent affecter le calcul. Sélectionnez un algorithme. En outre, divers modes de pondération et de mise à l'échelle peuvent être utilisés.

L'option de réglage la plus importante de cette page est la liste des valeurs initiales. Ici, vous pouvez déterminer les valeurs initiales des paramètres du modèle. En outre, vous pouvez déterminer si un paramètre a une valeur fixe ou non. Pour l'algorithme de Newton complet, une limite supérieure et inférieure peut également être spécifiée.

Le choix du paramètre initial est déterminant pour le calcul du résultat. Si le point de départ sélectionné est très éloigné du minimum global, l'algorithme peut ne pas renvoyer de résultat ou renvoyer un minimum local différent. Pour augmenter la probabilité qu'un minimum global figure dans le résultat affiché, le calcul doit être effectué avec différentes valeurs initiales. Pour les modèles comportant quatre paramètres ou moins, l'option Estimer les paramètres initiaux est disponible. Pour chaque paramètre, on calcule 10 valeurs distribuées aléatoirement qui se trouvent dans l'intervalle déterminé par les limites supérieure et inférieure. Pour chaque combinaison, la somme absolue des carrés résiduels est maintenant calculée. La combinaison avec la somme moyenne des moindres carrés fournit les valeurs initiales. Les valeurs initiales des paramètres peuvent également être calculées à l'aide d'une formule FPScript. Les critères de terminaison de l'algorithme peuvent être affectés par les options de paramétrage Appels maximum de fonction, Tolérance X, Tolérance Y, Tolérance F et Tolérance G. Le calcul de la première itération dépend des paramètres de la limite de pas.

Sur la dernière page de l'assistant, vous déterminez quels graphiques, tableaux et documents doivent être configurés en plus de l'objet d'analyse pour l'évaluation. Sélectionnez l'option Graphiques et tableaux présentant les résultats pour générer les graphiques et les tableaux affichés dans le volet Aperçu. Si vous souhaitez afficher la matrice de covariance, la matrice de corrélation, l'erreur standard des paramètres et les intervalles de confiance des paramètres sous forme de tableau, sélectionnez l'option supplémentaire Résultats numériques facultatifs. Cliquez sur le bouton Terminer pour fermer l'assistant.

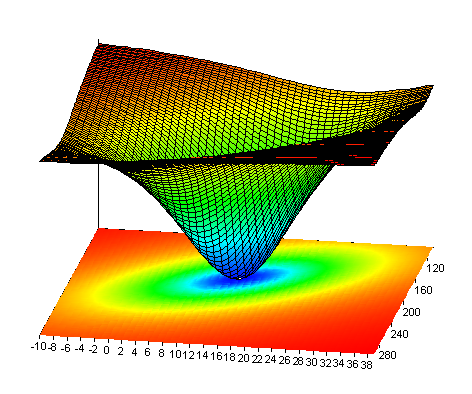
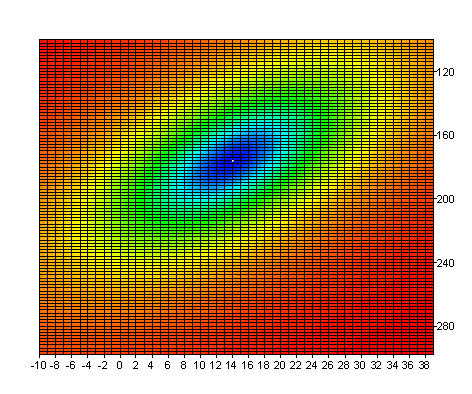
Maintenant, pour illustrer qu'un minimum local est présent dans le résultat, dans la formule Surface, la somme absolue des carrés résiduels est calculée pour le modèle. Les paramètres p0 et p1 sont variables ; les paramètres p2, p3 et p4 sont fixes. Le résultat est affiché dans le graphique de surface Surface. Il est important de noter que le minimum est à p0 = 14 et p1 = 176.

Utilisation du script de démarrage

Cet exemple illustre comment vous pouvez utiliser le script de démarrage pour calculer les valeurs initiales des paramètres du modèle.

Ouvrez la formule Linéarisation décrite ci-dessus, sélectionnez le contenu de la formule (CTRL+A) et copiez le contenu dans le presse-papiers du système (CTRL+C). Sélectionnez le signal Ag.

Ouvrez l'assistant pour l'ajustement de courbe non linéaire et allez à la troisième page de l'assistant. Cliquez sur le bouton. Collez le code du script du presse-papiers dans le champ de saisie (CTRL+V). Cliquez sur Calculer pour tester le script. Le résultat est une série de données avec cinq valeurs à virgule flottante de 64 bits. Cliquez sur Appliquer pour accepter les valeurs calculées comme valeurs initiales. Si le nombre de valeurs calculées n'est pas égal au nombre de paramètres du modèle, les valeurs calculées ne seront pas appliquées. Au lieu de coller directement le code du script dans le champ de saisie, vous pouvez faire référence à une formule déjà créée en saisissant le nom de la formule dans le champ de saisie. Toutefois, le code n'est alors valable que tant que l'objet formule existe.

Modèle personnalisé

En plus des modèles prédéfinis, il est possible de définir vos propres fonctions de modèle et de déterminer comment les sauvegarder. L'exemple suivant illustre comment configurer un modèle personnalisé. Sélectionnez la commande Fichier > Ouvrir Base de données projet et ouvrez la base de données projet C:\Users\Public\Documents\Weisang\FlexPro\2021\Exemples\CurveFitting.fpd ou C:>Utilisateurs>Public>Documents publics>Weisang>FlexPro>2021 >Exemples>CurveFitting.fpd. Ouvrez le dossier intitulé Modèle personnalisé et double-cliquez pour ouvrir la formule Données. La formule calcule un signal en utilisant la fonction polynomiale y = p0 + p1x + p2x² + p3x³. Il s'agit d'un signal avec 1000 valeurs à virgule flottante de 64 bits.

Comme cette fonction modèle est linéaire, les paramètres peuvent être calculés à l'aide de la fonction FPScript Approximation (formule Approximation linéaire).

Pour déterminer les paramètres à l'aide d'un ajustement de courbe non linéaire, sélectionnez la formule de Données et cliquez sur Insérer[Analyses] > Assistant d'analyse. Sélectionnez la catégorie Ajustement de courbes, puis Ajustement de courbes non linéaires. Cliquez sur Suivant. Dans le champ Modèle, tapez le nom Poly3 pour un modèle personnalisé. Deux champs de saisie apparaissent, dans lesquels vous entrez les formules de la fonction modèle ou la formule des dérivées partielles de la fonction modèle. Tapez p[0] + p[1] * x + p[2] * x^2 + p[3] * x^3 dans la zone de texte de la fonction. p[0] à p[3] décrivent les paramètres particuliers du modèle. Dans la zone de liste Nombre de paramètres, sélectionnez la valeur 4. Cliquez sur Enregistrer le modèle pour sauvegarder le modèle sous le nom spécifié. Si un message d'erreur apparaît dans le volet d'aperçu au lieu des résultats souhaités, vous devrez augmenter le nombre maximum d'appels de fonction à la page suivante de l'assistant. Cliquez sur Suivant. Sélectionnez 300 appels de fonction.

Cliquez sur le bouton Retour. Pour s'assurer que les dérivées partielles ne sont pas calculées numériquement, mais plutôt analytiquement, vous devez entrer les formules des dérivées partielles dans la zone de texte Dérivées : [ 1, x, x^2, x^3 ]. Les dérivées partielles doivent être fournies sous forme de liste. Le résultat de l'estimation des paramètres du modèle est maintenant plus précis. En outre, le nombre d'itérations requises est considérablement réduit en utilisant l'algorithme de Newton complet grâce au calcul analytique des dérivées partielles. Cliquez sur Enregistrer le modèle pour sauvegarder à nouveau le modèle.

Vous pouvez également attribuer des noms aux paramètres. Ces noms apparaîtront ensuite dans la liste Valeurs initiales de la page suivante de l'assistant. Pour ce faire, vous devez modifier la formule, qui décrit la fonction du modèle personnalisé, de la manière suivante :

Dim p0 = p[0]
Dim p1 = p[1]
Dim p2 = p[2]
Dim p3 = p[3]
p0 + p1 * x + p2 * x^2 + p3 * x^3

La variable p0 est affectée à la variable p[0], et la variable p1 est affectée à p[1], etc. Veillez à ce que les affectations se fassent les unes après les autres. Cliquez sur Suivant pour afficher la liste des valeurs initiales avec les paramètres renommés.

Cliquez sur Terminer pour fermer l'assistant.

Références

•P.R. Bevington, D.K. Robinson. Data Reduction and Error Analysis for the Physical Sciences, 3e édition, McGraw-Hill, New York, 2003.

•G. A. F. Seber, C. J. Wild. Nonlinear Regression. Wiley, New York, 2003.

•Harvey Motulsky, Arthur Christopoulos. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. Oxford University Press, 2004.

Voir aussi

Assistant d'analyse

Objet d'analyse Ajustement de courbes non linéaires

Options de résultat statistique pour l'ajustement de courbes non linéaires

Modèles non linéaires