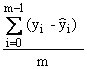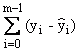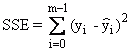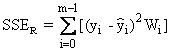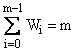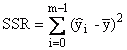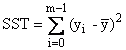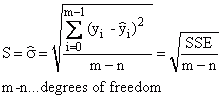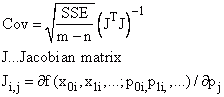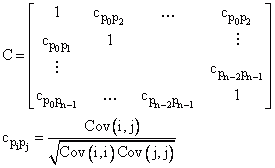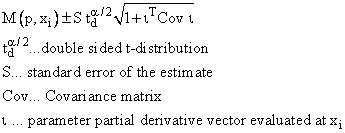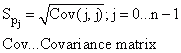Options de résultat statistique pour l’ajustement de courbes non linéaires
Toutefois, les critères de convergence ne suffisent pas à eux seuls à déterminer le résultat de l'ajustement non linéaire de la courbe. Un certain nombre de grandeurs statistiques sont disponibles pour vous aider à déterminer la qualité de l'ajustement.
Grandeur |
Calculé en utilisant |
Note |
|---|---|---|
Valeurs estimées / Les données modélisées |
|
Vous pouvez obtenir les valeurs estimées en calculant le modèle de régression sélectionné avec les paramètres p estimés. |
Résidus |
|
Les résidus sont la différence verticale entre les valeurs réelles des données et les valeurs estimées particulières. Si la valeur est positive, alors le point correspondant se situe au-dessus de la courbe estimée. Si la valeur est 0, alors le point se trouve sur la courbe. |
Moyenne Résiduelle |
|
Il s'agit de la valeur moyenne des résidus. |
Somme des résidus |
|
La somme peut être égale à 0 malgré de nombreux résidus positifs et négatifs. |
Somme résiduelle absolue des carrés |
|
|
Somme résiduelle relative des carrés |
avec |
Cette fonction est souvent décrite comme la fonction χ2 et constitue une mesure de la qualité de l'ajustement. |
Somme des carrés de régression |
|
|
Somme totale des carrés |
|
SST = SSE + SSR |
Variance d'erreur |
|
|
Coefficient de détermination multiple R2 |
|
R2 = 1,0 signifie que la courbe passe par chaque point de données. Avec une valeur x connue, la valeur y associée est déterminée avec précision. R2 = 0,0 signifie que le modèle de régression ne décrit pas mieux les données que sous la forme d'une ligne horizontale passant par la valeur moyenne des données. Les valeurs x connues ne sont d'aucune aide pour le calcul de la valeur y associée.
La seule évaluation de la valeur R2 n'est pas suffisante pour interpréter un modèle. Le meilleur ajustement de courbe est inutile si les paramètres déterminés n'ont pas de sens physique et/ou si l'intervalle de confiance est trop large.
|
Coefficient de détermination multiple ajusté Ra2 |
|
Avec ce coefficient, vous pouvez décider s'il vaut la peine d'augmenter le nombre de paramètres pour obtenir un R2 plus élevé. |
Matrice de covariance |
|
|
Matrice de corrélation |
|
Si les erreurs standard sont trop élevées et les intervalles de confiance trop larges, des recherches supplémentaires doivent être effectuées. L'une des causes pourrait être une redondance dans le modèle sélectionné, ce qui signifie que plusieurs paramètres du modèle sont en corrélation les uns avec les autres. Ici, la matrice de corrélation est utile. Pour les paramètres totalement non corrélés, vous ne pouvez pas compenser la détérioration de l'ajustement de la courbe, causée par la modification d'un paramètre, en adaptant l'un des autres paramètres. Vous pouvez cependant le faire pour des paramètres entièrement corrélés. Cela signifie également que les paramètres ne peuvent pas être clairement déterminés. Exemple : y = P0P1x |
Intervalle de confiance |
|
Le résultat est 95%, 99% et 99,9%. |
Bande de prédiction |
|
Le résultat est de 95%, 99% et 99,9%. |
Intervalle de confiance des paramètres |
est l'intervalle de confiance à 100(1-alpha)% pour un paramètre |
Il ne serait pas exact d'affirmer que pour un intervalle de confiance de 90 %, la probabilité qu'un paramètre se situe dans l'intervalle est de 90 %. Ce ne serait le cas que si vous disposiez d'un nombre infini de points de données. En d'autres termes, si vous répétez l'expérience sans cesse, alors 90% des intervalles de confiance contiendront le paramètre respectif. Le résultat est 95%, 99% et 99,9%. |
Erreur standard des paramètres |
|
|
et 
Qualité de l'ajustement
•Critères de convergence pour la détermination de la régression non linéaire :
Après chaque étape d'itération, la fonction doit être testée pour l'erreur moyenne la plus faible au carré (fonction χ²). Les paramètres nouvellement déterminés seront comparés au meilleur résultat obtenu jusqu'à présent. Si le nouveau paramètre calculé est meilleur, alors celui-ci est sauvegardé.
•Examinez le graphique de dispersion résiduel :
Les résidus doivent présenter une distribution aléatoire de 0 et aucun modèle reconnaissable. Si les résidus augmentent ou diminuent au fil du temps, par exemple, c'est le signe qu'un autre modèle serait meilleur ou qu'une pondération est nécessaire.
•Observez la courbe du modèle de régression :
Les valeurs des données doivent être distribuées de manière aléatoire au-dessus et au-dessous de la courbe.
•Vérifiez si le modèle sélectionné décrit bien les données :
οVérifiez R2 :
R2 = 1,0 signifie que la courbe passe par chaque point de données.
R2 = 0,0 signifie que le modèle de régression ne décrit pas mieux les données que sous la forme d'une ligne horizontale passant par la valeur moyenne des données.
•Somme résiduelle des carrés :
Un ajustement idéal de la courbe renvoie 0 comme résultat.
•L'erreur standard de l'estimateur est l'écart type des différences entre les données saisies et le modèle adapté. Cela vous donne un aperçu de la façon dont les résidus sont distribués par la valeur moyenne. Un ajustement idéal de la courbe renverrait la valeur 0.
•Vérifiez si les valeurs calculées ont un sens, par exemple, assurez-vous que vous n'avez pas contredit les lois de la physique.
•Observez l'intervalle de confiance.
Si l'intervalle de confiance est trop large, l'ajustement de la courbe ne sera pas clair. D'autres valeurs pourraient conduire à un résultat similaire.
•Il est possible de trouver le mauvais minimum. Cela pourrait être le cas s'il s'agit d'un minimum local, mais ce ne serait pas le cas pour un minimum global. Il est donc important de trouver de bonnes valeurs initiales pour le modèle sélectionné.
Plusieurs tests avec différentes valeurs initiales augmentent la probabilité que les résultats soient corrects.
Références
•P.R. Bevington, D.K. Robinson. Data Reduction and Error Analysis for the Physical Sciences, 3e édition, McGraw-Hill, New York, 2003.
•J. Hartung. Statistik. Lehr- und Handbuch der angewandten Statistik (Manuel de statistiques appliquées). 9ème édition. Oldenbourg Verlag, 1993.
•Harvey Motulsky, Arthur Christopoulos. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. Oxford University Press, 2004.
Voir aussi
Objet d'analyse Ajustement de courbes non linéaires